On the
Credible Interval under the Zero-Inflated Mixture Prior in High Dimensional
Inference:
In this paper, we consider the construction of the credible set under the
canonical Bayes model when assuming the parameter of interest θ follows a prior distribution
which is a mixture of zero with probability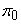 and another non-trivial distribution with probability and another non-trivial distribution with probability 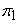 = 1− = 1−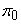 . In modern application with high dimension, . In modern application with high dimension, 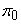 is usually very
large, implying that the posterior probability P(θ = 0| X) is also
large, saying greater than 5%. The traditional approaches constructing 95%
posterior credible intervals, such as HPD region or the equal-tail credible
interval, will enclose zero very
often and appear to be powerless. is usually very
large, implying that the posterior probability P(θ = 0| X) is also
large, saying greater than 5%. The traditional approaches constructing 95%
posterior credible intervals, such as HPD region or the equal-tail credible
interval, will enclose zero very
often and appear to be powerless.
In
this paper, we use the decision Bayes approach to guide us constructing a
mixture credible interval. When there is overwhelming evidence that 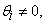 we scrutinize the
distribution we scrutinize the
distribution 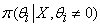 and consider the HPD
region. Otherwise, the interval is the union of such a HPD region and zero. The paper provides a systematic
way in deciding when to include zero,
guaranteeing the average coverage probability. and consider the HPD
region. Otherwise, the interval is the union of such a HPD region and zero. The paper provides a systematic
way in deciding when to include zero,
guaranteeing the average coverage probability.
We
apply this general approach to a normal mean problem with unknown and unequal
variances and apply it to a real data set. It is demonstrated that the new
approach is way more powerful than the traditional and other alternatives.
Assistant Professor Zhigen (Gene) Zhao,
Department of Statistics, Temple University, Philadelphia,
PA, 19122
~ September 9, 2011
|
|
Mining
Port-level IP Data:
In this paper, we look at and resolve some issues involved
in analyzing IP traffic at the port level. For example, we develop a mapping
between alternative ways of measuring circuit utilization and describe a
method of normalizing utilization to accommodate changes in bandwidth. We
also prescribe a class of patterns that is suited to analyzing utilization
for a large number of circuits in a dynamic environment.
Errol C Caby,
PhD, AT&T Labs Research, Florham Park, NJ
~ September 15, 2011
|
|
Continuously Additive Models for Functional Regression:
We propose Continuously Additive Models (CAM), an extension of additive
regression models to the case of infinite-dimensional predictors,
corresponding to smooth random trajectories, coupled with scalar responses.
As the number of predictor times and thus the dimension of predictor vectors
grow larger, properly scaled additive models for these high-dimensional
vectors are shown to converge to a limit model, in which the additivity is
conveyed through an integral. This defines a new type of functional
regression model. In these Continuously Additive Models, the path integrals
over paths defined by the graphs of the functional predictors with respect to
a smooth additive surface relate the predictor functions to the responses.
This is an extension of the situation for traditional additive models, where
the values of the additive functions, evaluated at the predictor levels,
determine the predicted response. We study prediction in this model, using
tensor product basis expansions to estimate the smooth additive surface that
characterizes the model. In a theoretical investigation, we show that the
predictions obtained from fitting continuously additive estimators are
asymptotically consistent. We also consider extensions to generalized
responses. The proposed estimators are found to outperform existing
functional regression approaches in simulations and in applications to human
growth and yeast cell cycle data.
Assistant Professor, Yichao Wu, Department of Statistics, North Carolina
State University, Raleigh, NC 27695-8203 ~ October 6, 2011
|
|
Model-based Prediction of Solar Particle
Events:
Astronaut health may be at risk with exposure to high energy solar
particle events (SPEs). This becomes a major concern during extra-vehicular
activities (EVA) on the lunar and Mars surface. In this talk, I will present
model based predictions used to optimize planning for future space missions.
SPEs are modeled as a function of time within a solar cycle. A
non-homogeneous Poisson model is applied on historical data on solar events
occurring between 1954 and 2006. Statistical modeling results will be shown
for prediction of frequency and severity of solar events.
Assistant Professor Matt Hayat ,
Biostatistician, College of Nursing, Rutgers University, Newark, NJ ~ October
20, 2011
|
|
Algebraic
Statistics and Applications to Statistical Genetics:
When testing independence in the context of contingency tables, the
chi-squared test is a boon. However, this is an asymptotic test the use of
which requires certain conditions to be fulfilled. If the chi-squared test is
not justified, one could use Fisher's exact test. Even the use of Fisher's
exact test is fraught with enormous computational difficulties. To set the
stage for the talk, I set about explaining how algebraic statistics softens
computational issues. Similar computational difficulties arise when one sets
about testing a la Fisher Hardy-Weinberg equilibrium on a multi-allelic
marker. I will demonstrate how algebraic statistics in conjunction with
Markov bases and MCMC solves the problem. If time permits, I will ruminate on
triad designs in genetics and gene-environment interactions.
Professor M. Bhaskara Rao, University
of Cincinnati Medical Centre,
Cincinnati, OH 45267 ~ October 27, 2011
|
|
Exploratory
Analysis of Large-Scale Spatial-Temporal Data:
AT&T's Mobility data related to voice and data usage has a spatial
(cell sites in different geographies) as well as a temporal component (usage
collected at regular intervals). The focus of this work is to develop tools
for exploratory data analysis as it relates to spatial data. The exploratory
analysis techniques will look at both spatial and temporal aspects
independently and also the attributes of their joint (spatial-temporal)
behavior. Visualization techniques in particular to identify outliers (local
and global), pockets of non-stationarity and other additional insights that
are not otherwise apparent will be demonstrated. Some examples from the
AT&T data will be provided.
Ganesh K. (Mani) Subramaniam, PhD.,
AT&T Labs - Research, Florham
Park, NJ ~ November
3, 2011
|
|
Valid
Post-Selection Inference:
It is common practice in statistical data analysis to
perform data-driven model selection and derive statistical inference from the
selected model. Such inference is generally invalid. We propose to produce
valid “post-selection inference” by reducing the problem to one of
simultaneous inference. Simultaneity is required for all linear functions
that arise as coefficient estimates in all submodels. By purchasing
“simultaneity insurance” for all possible submodels, the resulting
post-selection inference is rendered universally valid under all possible
model selection procedures. This inference is therefore generally
conservative for particular selection procedures, but it is always less
conservative than full Scheffe protection. We describe the structure of the
simultaneous inference problem and give some asymptotic results.
Kai Zhang, Department of Statistics, The
Wharton School, University of Pennsylvania, Philadelphia, PA 19104 ~ November
10, 2011
|
|
Optimal Multiple Testing Procedure Incorporating Signal Strength:
This research focuses on incorporating signal strength into a multiple
testing procedure using a decision theoretic approach. Specifically, we
propose a general loss function which incorporates the severity of Type II errors.
We also propose error rates that incorporate signal strength: the weighted
marginal false discovery rate and the weighted marginal false nondiscovery
rate. We then derive optimal procedure which minimizes the weighted marginal
false nondiscovery rate, while controlling the weighted marginal false
discovery rate. The numerical studies show that, by incorporating signal
strength, much power can be gained.
Dr. Li He, Department of Statistics, Temple University,
Philadelphia, PA, 19122
~ November 16, 2011
|
|
High-Dimensional
Variable Selection in Meta Analysis for
Censored Data:
This talk considers the problem of selecting predictors of time to an
event from a high-dimensional set of candidate predictors using data
from multiple studies. As an alternative to the current multi-stage
testing approaches, we propose to model the study-to-study
heterogeneity explicitly using a hierarchical model to borrow strength.
Our method incorporates censored data through an accelerated failure
time (AFT) model. Using a carefully-formulated prior specification, we
develop a fast approach to predictor selection and shrinkage estimation for
high-dimensional predictors. For model fitting, we develop a Monte Carlo
Expectation Maximization (MC-EM) algorithm to accommodate censored data.
The proposed approach, which is related to the relevance vector machine
(RVM), relies on maximum a posterior (MAP) estimation to rapidly obtain a
sparse estimate. As for the typical RVM, there is an intrinsic threshold
property in which unimportant predictors tend to have their coefficients
shrunk to zero. We compare our method with some commonly used procedures
through simulation studies. We also illustrate the method using the gene
expression barcode data from three breast cancer studies.
Fei Liu, PhD, Research Staff Member,
Statistical Analysis & Forecasting, Business Analytics & Mathematical
Sciences, IBM Thomas J. Watson Research Center Yorktown Heights, NY 10598 ~
December 1, 2011
|
|
K-scan for anomaly detection in spatial
point patterns:
We
consider the problem of detecting hotspots in spatial point patterns observed
over time while accounting for inhomogeneous background intensity. For
example, in disease surveillance, the interest is often in identifying
regions of unusually high incidence rate given a background incidence rate
that may be spatially varying due to underlying variation in population
density, say. I will present a K-scan method that uses components of the
inhomogeneous K function to identify such anomalies or hotspots. The significance
of detected hotspots is assessed using either bootstrap or a p-value
approximation based on a Gumbel distribution. I will show some results from a
simulation study, as well as applications of this method to dead bird
sighting data from Contra Costa county in California
and to fast food restaurant location data in New York City.
Ji Meng Loh, PhD., AT&T Labs - Research, Florham Park, NJ
~ December 08, 2011
|