| Physics 321 |
Astrophysics II: Lecture #5
|
Prof. Dale E. Gary
NJIT
|
Classification of Spectra,
and Hertzsprung-Russell Diagrams
Spectra from the Hydrogen
Atom
The Bohr model of
the hydrogen atom gave us the following results:
-
The angular
momentum, l, was postulated
to be quantized according to
l = mvr = nh/2p.
where n is the principle quantum
number.
-
The radii
of allowed electron orbits were also quantized according
r = aon2
= n2h2/(4p2ke2m)
where
ao=
5.29 x 10-11
m is the Bohr
radius.
-
The energies of the orbits were
likewise quantized according to
where R' = 13.6
eV
is a constant. The electron-volt
(eV)
is a unit of energy (the energy an electron would gain after acceleration
through a potential of 1 volt). 1 eV
= 1.602 x 10-19
J
-
The difference between energy
levels (orbits) corresponds to a wavelength
1/lab
= nab/c
= (Eb -
Ea)/ch=R [1/nb2-1/na2]
where R = 10.96776
mm-1
is the Rydberg constant.
One way to see why the angular
momentum should be quantized is to consider the electron as a wave.
As de Broglie showed, particles exhibit wave characteristics with wavelength
given by
l
= h/p = h/mv
What if the lowest orbit corresponded
to one wavelength of such an electron wave? The circumference of
the orbit would correspond to a wavelength, so
2pr
= l = h/mv
=> l = mvr = h/2p.
The next
higher orbit would correspond to two electron wavelengths, and the nth
orbit to n
electron wavelengths, so in this way we naturally find l
= nh/2p.
If the orbit corresponded to a non-integer multiple of the electron wavelength,
the electron wave would overlap and interfere with itself.
Here
is a scale model of the orbits of the hydrogen atom, with the radii getting
further apart according to n2:
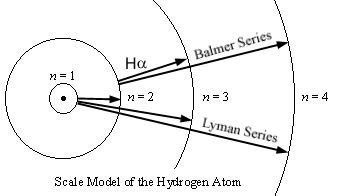
However, despite the orbits
getting ever farther apart in space, they get closer together in energy
according to 1/n2.
Any energy level diagram is shown below:
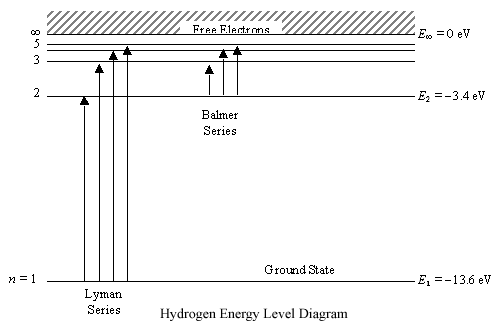
Excitation, De-excitation, Ionization
and Recombination
When an electron
jumps from a lower energy level to a higher energy level (smaller n
to larger n), the atom is said to be excited, and the process is
called excitation. Energy must
be added to the atom in order for such a jump to occur. There are
two ways for an atom to be excited:
-
If the atom suffers a collision
that causes an electron to jump from the lower to higher energy state it
is called collisional excitation.
-
If the electron captures a photon
of energy hn
corresponding to the energy difference between the two energy levels, and
so jumps from the lower to higher energy state, it is called radiative
excitation.
There are also two reverse processes
by which the electron can jump from the higher energy level to a lower
one, in the process of de-excitation.
These are:
-
If the atom suffers a collision
that causes an electron to jump from a higher to lower energy state it
is called collisional de-excitation.
-
If the atom jumps from a higher
to lower energy state and emits a photon of energy hn
corresponding to the energy difference between the two energy levels, it
is called radiative de-excitation.
Since energy is released during such a transition, the transition is spontaneous,
meaning it occurs without any outside action.
In addition to electrons jumping
up and down between energy levels in the atom, it is possible for an electron
to jump completely away from the atom (ionization),
or a free electron to be captured into an energy level (recombination).
Heisenberg Uncertainty Principle
We noted last time
the relationships:
DxDp
~ h/2p
DED
t
~ h/2p
but did not have time to show
some effects that come from them. The n = 2
level of hydrogen lives for a very short time, only about 10-8
s. That is, an electron in the first excited state will, after about
10-8 s, spontaneously emit a photon of
energy 10.2 eV and go back to the ground state (emitting a Lyman a
photon). The second relation, above, means that the photons emitted
have an energy uncertainty of
DE ~ h/2pD
t
=
1.05 x 10-26 J => Dl
~ l2/2pD
t
c = 0.014 mA
This uncertainty
in the wavelength shows up as a broadening of the spectral line (natural
broadening).
Similarly, we can ask what
is the uncertainty in speed that is required of an electron that is confined
in a hydrogen atom (in the ground state orbit, with Bohr radius ao=
5.29 x 10-11
m).
Example: Imagine
an electron comfined within a region of space the size of a hydrogen atom.
What is the minimum speed and energy of the electron, estimated using the
Heisenberg uncertainty principle? We know Dx
~ ao=
5.29 x 10-11 m
so
Dp ~ h/2pao
= 6.62 x 10-34
J s/2p(5.29 x 10-11
m)
= 1.99 x 10-24
kg
m/s.
This is
the uncertainty in the momentum, which is about equal to the minimum momentum
pmin
that the electron has in order to be confined within the atom. Now
the momentum is just p = mv,
so the minimum velocity is
vmin
= pmin/me
= 1.99 x 10-24
kg m/s / 9.1 x 10-31
kg = 2.19 x 106
m/s.
The corresponding minimum kinetic
energy is
Kmin
= 1/2mev2min=
2.18 x 10-18
J
which may seem like a small
energy, but when converted to electron volts, this is
Kmin
= 2.18 x 10-18
/ 1.602 x 10-19
J/eV = 13.6 eV!
This is exactly the energy of
an electron in the ground state of the hydrogen atom! Later we will
see that this subtle quantum effect is responsible for supporting the tremendous
gravitational weight inside a white dwarf star.
Spectral Classification
When spectra of stars are
examined, spectral lines are easily seen, and the lines of the Balmer series
for hydrogen are particularly recognizable. The first spectral classification
simply ordered stars according to how strong the H-Balmer lines were (Pickering
and Fleming), as A, B, C, ... See the spectra below.

Adapted from data in the electronic version of "A Library of Stellar
Spectra,"
by Jacoby G.H., Hunter D.A., Christian C.A. Astrophys. J.
Suppl. Ser., 56, 257 (1984).
The spectra were then reordered
according to temperature using the
continuum spectrum (blackbody curve) as a guide (Annie Jump Cannon), to
arrive at a new ordering:
O, B, A, F, G, K, M
(Oh Be A Fine Girl/Guy Kiss Me)
(early)
(late)
...B7, B8, B9, A0, A1, A2,
A3, ..., A7, A8, A9, F0, F1... etc.
(early A)
(late A)
It is puzzling, however, that
the hydrogen lines should get stronger as we go into the sequence, then
get weaker again. They reach their greatest strength at A0, which
is a blackbody temperature of about 9500 K. Why should this be?
Strength of Spectral Lines
Background:
-
The Balmer series are transitions
from/to level 2 of the neutral hydrogen atom.
-
We expect the lines to be strongest
when lots of atoms have electrons in level 2 => high temperature.
-
However, if the temperature
is too high, the atom can be ionized (the electron is stripped off).
-
Ionization notation: H
I = neutral hydrogen
H II =
ionized hydrogen
He I = neutral
helium
He II = singly-ionized
helium
He III = doubly-ionized
helium
These are called ionization
stages.
To understand the behavior of
the line strength with temperature, we must answer the following two questions:
-
how does
the population of levels depend on T?
-
how does
ionization depend on T?
Statistical Mechanics
These questions
can be answered by appealing to statistical mechanics. Imagine firing
a beam of particles, all with the same energy, into a trap and allowing
them to come into equilibrium by colliding elastically. Due to standard
probability and statistics (akin to coin-tossing), they will wind up with
a gaussian distribution of speeds (a bell curve). Any distribution
of particles in equilibrium will have such a curve, which can be
parametrized by a single number, the temperature. Due to the
3D nature of velocity, the gaussian when expressed in terms of speed becomes:
nv dv
= n (m/2pkT)3/2exp(-1/2
mv2/kT )(4pv2)
dv
where the important dependence
is the argument of the exponential, which is just the ratio of the kinetic
energy (1/2 mv2)
to thermal energy (kT ).
This expression is the number of particles per unit volume having speeds
between v and v +
dv.
Important relationships:
-
Peak of distribution (most probable
speed) is when 1/2 mv2 =
kT,
or
-
Mean speed is somewhat higher
(due to asymmetry in the curve)
Boltzmann Equation
As atoms collide,
their electrons can be knocked up to the next higher energy level if the
colliding atoms have enough energy (collisional
excitation). The electron can even be knocked entirely
away from the atom (ionization).
Again, looking at the problem from a statistical standpoint, the probability
of the atom's being in one energy state, sa,
is
P(sa)
~ exp(-Ea/kT
)
and the probability for state
sb
is
P(sb)
~ exp(-Eb/kT
)
where Ea
and Eb
are the energies of the two states (e.g. = 13.6 eV
for the ground state of the hydrogen atom). The ratio of these probabilities
is then
| P(sb) |
|
exp(-Eb/kT
) |
|
= |
|
| P(sa) |
|
exp(-Ea/kT
) |
However, more than one state
in an atom can have the same energy (i.e. they can be degenerate),
e.g. in He I (neutral helium) two electrons in the ground state have n
=
1, but the two electrons spin in opposite
directions (ms = +1/2, -1/2).
We define the degeneracy (the number of states with the same energy Ea)
as ga,
which is called the statistical weight of
state a. The above expression
then becomes
| P(sb) |
|
gb exp(-Eb/kT
) |
|
= |
|
| P(sa) |
|
ga exp(-Ea/kT
) |
For a large number of atoms,
the ratio of probabilities must be the same as the ratio of numbers of
atoms in the two energy levels, e.g.
| Nb |
|
gb |
|
|
= |
|
exp(-[Eb-Ea]/kT
) |
| Na |
|
ga |
|
This is the Boltzmann
Equation. It turns out that for hydrogen, the statistical
weights are given by gn=
2n2.
The Boltzmann Equation answers the first question we had, namely, how does
the population of levels depend on T.
However, if we want to populate level 2 to make strong H-balmer lines,
what temperature do we need, say, to make as many level 2 atoms as there
are level 1 atoms? The equation becomes
| N2 |
|
8 |
|
|
= |
|
exp(-[E2-E1]/kT
)
= 4 exp(-[-10.2
eV+13.6 eV]/kT ) = 1 |
| N1 |
|
2 |
|
but when we solve for T
we find T ~ 85,000 K!
Much higher than the observed 9,500 K. Clearly there is another important
effect that we did not include. That other effect is ionization.
Saha Equation
To get a hydrogen
atom's electron into level 2, it required a collision with at least 10.2
eV of energy. However, once it is in level 2, it requires only 3.4
eV more energy to knock it completely away from the atom, so the first
excited state is a very precarious place for an electron! The actual
number of atoms in level 2 at any one time is a balance between collisions
to get it there in the first place, and collisions to ionize the atom.
Let ci
be the ionization potential of the
ith
ionization stage. This is the amount of energy needed to remove an
electron from its lowest energy state. For the ionization stage H
I, for example, it would be 13.6 eV.
For He I it would be roughly the same, but for He II it would be four times
larger (why?). You might think that the ratio of atoms in one stage
relative to another would be
| Ni+1 |
|
|
|
~ |
exp(- ci
/
kT
) |
| Ni |
|
|
which is nearly right, but
not all of the atoms are in this lowest state, so we have to add up statistically
all of the ways an atom in various energy states can be stripped of an
electron.
Partition Function
| |
|
infinity |
| Zi |
= |
S
g1
exp(-[Eb-Ea]/kT
) |
| |
|
1=1 |
where the sum is over the
distribution of energy states of an atom at temperature T from the
Boltzmann Equation.
Then
| Ni+1 |
|
Zi+j
|
|
|
~ |
|
exp(- ci
/
kT
) |
| Ni |
|
Zi
|
|
which leads to the Saha Equation
| Ni+1 |
|
2Zi+j
|
( |
2pmekT |
) |
|
= |
|
|
exp(- ci
/
kT
) |
| Ni |
|
neZi
|
h2
|
|
Example: Saha Equation
for H between 5,000 and 25,000 K.
Partition function for H
II is ZII= 1,
since there is no degeneracy for a bare proton. For H I the summation
can be done over just two terms (why?) which gives
ZII= 2 + 8 exp(-[(-10.2
eV)-(-13.6 eV)]/kT
) = 2 + 8 exp(-3.4
eV/kT
)
Now, writing the thermal energy
in eV, we have the range ~ 0.5 to 2.5 eV, so the exponential term ranges
from about 8(0.001) to 8(0.25), so
ZII= 2 to 4
over the temperature range.
What we really want is not NII/NIas
given by the Saha equation, but a related quantity NII/Ntotal
=
NII/(NI+NII)
= NII/NI /
(1+NII/NI)
which is plotted in Figure 8-13 in the text (curve labelled log
N+/No).
You can see that almost all of the H will be ionized by about 10,000 K.
This is what limits the strength of the H-balmer lines above 9,500 K.
Combining the Boltzmann and
Saha Equations
We can find the
variation of the strength of the H-alpha line with temperature by combining
the Boltzmann and Saha equations as follows:
|
N2
|
|
N2
|
|
NI
|
|
= |
|
|
|
| Ntotal |
|
N1+N2
|
|
Ntotal |
or
|
N2
|
|
N2/N1
|
|
NI
|
|
N2/N1
|
|
1
|
|
= |
|
|
|
= |
|
|
|
| Ntotal |
|
1+N2/N1
|
|
NI+NII |
|
1+N2/N1 |
|
1+NII/NI |
The final expression is written
entirely in terms of the quantities provided by the Boltzmann and Saha
equations. The full dependence is plotted in Figure below, and in
Fig. 8-13 of the text. Here we see very nice confirmation of the
observed strength of the hydrogen lines, since the curve peaks right near
10,000 K as required to match the observations.
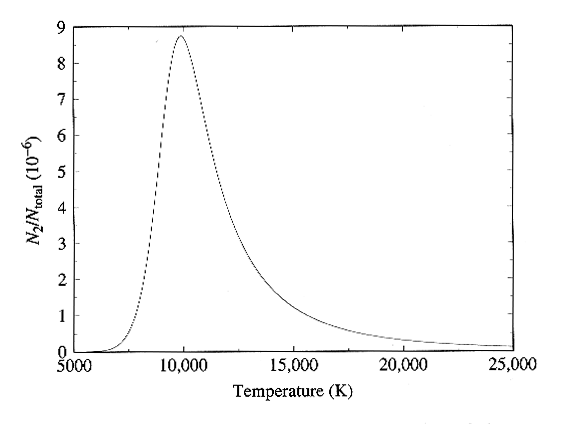
Ratio of hydrogen atoms in the n = 2 level to the total number
of hydrogen atoms
as a function of frequency. Figure from Carroll and Ostlie, Modern
Astrophysics,
Addison-Wesley Publishing Co., 1996.



