Physics 728
Radio Astronomy:  Lecture #4
Prof. Dale E. Gary
NJIT

Primary Antenna Elements

Introduction

The antennas of an array have two main purposes:
The first function of the primary element can be expressed in terms of the antenna effective area, A(ν, θ, φ), in units of m2, where θ, φ are direction coordinates on the sky.  If the brightness of a source is I(ν, θ, φ) in W m−2 Hz−1 ster−1, then the power collected, in W, is found by integrating over solid angle ΔΩ and bandwidth Δν and multiplying by the collecting area:
 
P = A(ν, θ, φ)  I(ν, θ, φ) ΔΩ Δν
flux density
 (W m−2 Hz−1)
flux
 (W m−2)
Associated with the collecting area (effective area) is the beam pattern, also called the primary beam, which is just the Fourier Transform of the aperture, as shown in the figure below.


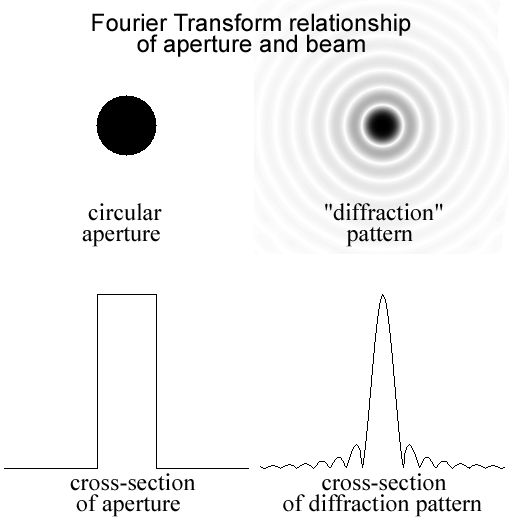
Figure 1.

We will come back to the primary elements, and the beam pattern, or primary beam, shortly.  But first, let's take a closer look at Fourier Transforms.

Fourier Transform Relationship and Inverse
This is the first time we have explicitly met the Fourier Transform relationship, but since it occurs over and over in radio astronomy, it is worthwhile to look at it in some detail, in particular the Fast Fourier Transform.  You are encouraged to experiment with the FFT function in IDL (Interactive Data Language), Python, or other scientific computing package you may have.

Given two spatial coordinates, x, y, in m, say, we consider the corresponding spatial frequencies, u, v, in wavelengths, defined as u = x/λ, v = y/λ.  Then F(l,m) is the fourier transform of f(u,v):

 
2pi(ul + vm)
F(l,m) =  f(u,v) e du dv
aperture
where The inverse is written as
 
−2πi(ul + vm)
f(u,v) =  F(l,m) e dl dm
all sky

and you would perform this inverse with the FFT by using fft(F, −1) (ifft2 in Python) where the −1 indicates the inverse Fourier Transform. Note that the definition of the IDL FFT (and others) defaults to −1, so fft(F) = fft(F, −1). If you want the forward transform, you will have to do fft(F, 1).

We are going to use Fourier Transforms further in discussing the response of pairs of antennas (interferometer baselines), which we will do in Lecture 6.  Let's go ahead and introduce that now.  A pair of antennas measures one point in the u,v plane, and the Fourier Transform of this point gives the familiar interference fringes on the sky.

These relationships are shown graphically in the figure below:


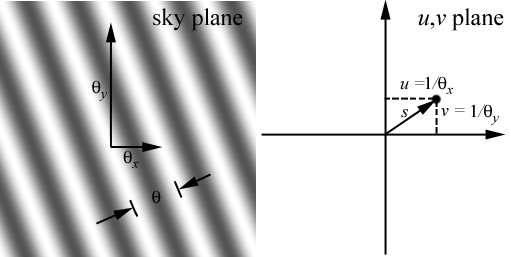
A point in the u,v plane a distance s from the origin has components u and v.
In radio astronomy, this corresponds to a single baseline, or pair of antennas.
The FT of this sampling corresponds to fringes in the sky plane, with angular
separation θ = fringe spacing.  The two corresponding angular coordinates are
θl and θm, which are the fringe separations in the l and m angular directions.

The following terminology is used

  • s = (u2 + v2)1/2 = spatial frequency
  • s−1 = θ = fringe spacing
  • u = "x-component" of s
  • v = "y-component" of s
    • When we use FFT's, of course, we must pixelize, or grid, the data into 2-d arrays that the computer can deal with.  The first step, then, is to pick a pixel size for the u,v plane.  Let's look at the antenna aperture problem, and consider an antenna of 6 m aperture.  Note that we also have to know what frequency (wavelength) we want to consider.  At 5 GHz, the wavelength is 6 cm, so 6 m is 100 wavelengths (we can say that the dish diameter is Dλ = 100).  We might choose a pixel size corresponding 1 wavelength, so that our aperture will occupy a circle of radius 50 pixels (diameter 100 pixels).  After we do the FFT, what is the corresponding pixel size in the sky plane (also called the map)?

    If you step into the first pixel in the u,v plane, this corresponds to one cycle (one fringe) fitting across the entire map.  The second pixel corresponds to two cycles fitting across the map, and so on.  We said the fringe spacing was s-1, so stepping one pixel (s = Δs) yields a fringe spacing of θ = NΔθ = 1/Δs (radians), where N is the number of points in the array.  Thus, for a u,v array of 256 points, with each pixel in the array representing 1 wavelength, we will have each pixel in the map corresponding to

    Δθ = (NΔs)−1 = 1/256 radian = 13.4 arcmin.
    So how many pixels should the beam be?  We said in the first lecture that the beam was θ ~ λ/D = 1/Dλ, which is 0.01 radian, or 35 arcmin, so the beam will occupy less than three pixels!  Here is the result:

    ap = float(dist(256) le 50.)                 beam = fft(ap)    [IDL]
    ap = (dist(256) <= 50.).astype(float)      beam = ifft2(ap)   [Python]
    The IDL and Python commands used to create the above two images, are shown
    just below each image.

    So to see the beam shape in better resolution we have two choices--use a larger Δs, or use a larger array (larger N).  Here is the result using array size of 1024:

    It may seem paradoxical that we can put the same size circular aperture into a larger array full of blank space, and get a higher resolution view of the beam shape, but that is the way it works.  Note that we have the following useful relations:

    Δθ = (NΔs)−1    (relation between pixel sizes in the two planes)
    NΔθ = Δs−1       (relation between map sizes in the two planes)
    These are symmetrical:
    Δs = (NΔθ)−1    (relation between pixel sizes in the two planes)
    NΔs = Δθ−1       (relation between map sizes in the two planes)
    Note also that the smallest fringe spacing possible is one in which every other pixel is a peak (i.e. N/2 fringes across the map).   This is the Nyquist frequency, and corresponds to the largest useful distance in the u,v plane, e.g. u = N/2.  If you try to go beyond u = N/2, the point "wraps around" and becomes u = −N/2.
    Back to the Primary Beam
    The "power pattern" of a single dish telescope is |F(l,m)|2, i.e., the beam pattern is the square of the complex far-field voltage pattern, |F(l,m)|2 = F(l,m)F*(l,m).  Here is a plot of the angular pattern:
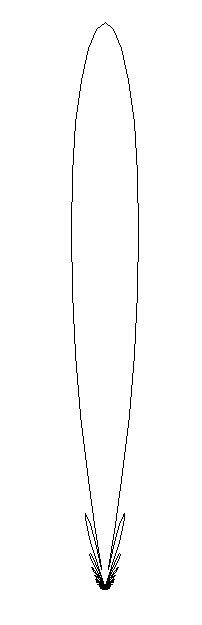    where you can see the main lobe and the side lobes.  This pattern is, of course, azimuthally symmetric.  The dish is maximally sensitive to radiation from the direction of the peak of the beam, but is also slightly sensitive to sources in the side lobes.  If we write A(ν, θ, φ) for the collecting area, as before, then we can normalize to the peak value on-axis, A(ν, 0, 0) = Ao and consider the normalized beam pattern A(ν, θ, φ) = A(ν, θ, φ) / Ao.  Then the beam solid angle is
    ΩA =  A(ν, θ, φ) ΔΩ
    all sky

    Directivity
    An isotropic antenna would have solid angle ΩA = 4π.  The directivity (also called the gain of the antenna) is defined as the ratio of peak radiation intensity to average radiation intensity

    D = 4π / ΩA
    so a highly directive antenna has a small ΩA.

    Collecting Area vs. Physical Area
    Ao is the collecting area when pointed directly at a source, yet this may not be the same as the physical area of the aperture.  The ratio can be used to define an aperture efficiency η < 1

    Ao = ηA
    which takes into account a variety of losses.  We will come back to this shortly.

    A fundamental relationship between Ao and ΩA is

    AoΩA = λ2
    which shows that as Ao gets bigger, ΩA gets smaller (D = directivity increases).

    Antenna Types
    At wavelengths below ~ 1 m (300 MHz), simple wire antennas (e.g. dipoles, yagis, spirals, etc.) can be used.  Note that we can define the collecting area of a dipole as

    Ao = λ2/ΩA
    and use the dipole radiation pattern, proportional to sin2θ to determine ΩA.  Other combinations, such as a yagi antenna, have a different radiation pattern, but the relationship can still be used.

    At short wavelengths, wires give too small a collecting area, so reflecting surfaces are used.  We will concentrate on reflecting dishes from here on.  A useful rule of thumb is that when the wavelength grows so large that a dish is less than 5 wavelengths in diameter, the dish is no longer competitive with the same size dipole.  That means a 2 m dish, for example, is only effective to wavelengths shorter than 40 cm => frequencies higher than 750 MHz.

    See Napier lecture for examples of types of antennas.

    Antenna Performance
    Aperture Efficiency
    As we said a moment ago, the aperture efficiency Ao = ηA is made up of several factors.  In general, we can write the efficiency as the product of several factors
    η = ηsf ηbl ηs ηt ηmisc
    where
    ηsf = reflector surface efficiency
    ηbl = reflector blockage efficiency
    ηs = feed spillover efficiency
    ηt = illumination efficiency
    ηmisc = losses due to reflector diffraction, feed position errors, feed mismatch, and others
    See Napier lecture for discussion of reflector surface efficiency.

    Aperture Blockage Efficiency
    Many antenna designs (prime focus and cassegrain), require structures to hold the feed and/or subreflector in place, and these structures block part of the aperture.  The situation is shown in the figure below, and can be analyzed by considering different parts of the structure separately, e.g. regions 1, 2, 3 and 4 in (b), and doing the Fourier Transform of each part.  Thus, (c) is the FT of the unblocked aperture, (d) is the FT of part 2 (shown negative because it is a blockage), (e) is the FT of part 3, also negative, (f) is the FT of part 4, and finally (g) is the sum of the FT's.  The reason one can separately treat each part is because the FT procedure is linear.  This is a very important property that we will use several times in the course.

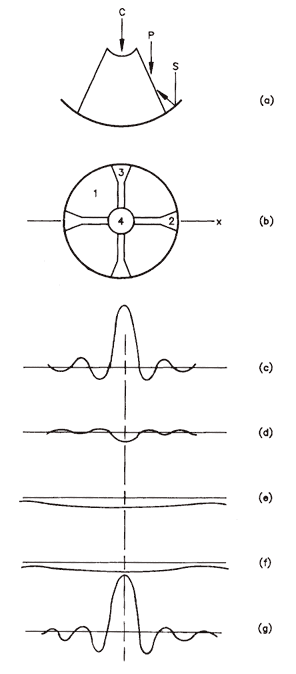    The efficiency due to blockage is
    ηbl = (1 − area blocked/total area)2 ~ (1 − 2*area blocked / total area)  for small blocked / total.
    Note that the blockage affects the beam shape in addition to the aperture efficiency.  Some designs are off-axis to reduce or eliminate blockage (but this may cause other unwanted effects).

    Feed Spillover Efficiency
    Consider the antenna as a transmitter.  For a prime focus antenna, spillover efficiency is the fraction of radiated power intercepted by the reflector.  Power not intercepted is lost.  Telescopes for radioastronomy often have F/D = 0.4, so the half-angle that the dish presents as viewed from the feed is θR = atan 0.5/0.4 = 51o, so the total width is about 100o.  Thus, we need a broad feed pattern to illuminate the dish.  Note that any spillover "sees" the ground in receiving mode, and that can increase the noise temperature, which we will discuss later.

    The situation is different for a Cassegrain design, where the feed is at the reflector and the radiation has to hit the subreflector (secondary).  In that case, θR is much smaller, so we need to use a more directive feed.  In this case, spillover "sees" the sky.

    Typically, 0.7 < ηs < 0.97, with the higher values requiring "shaped" reflectors as in the figure below.


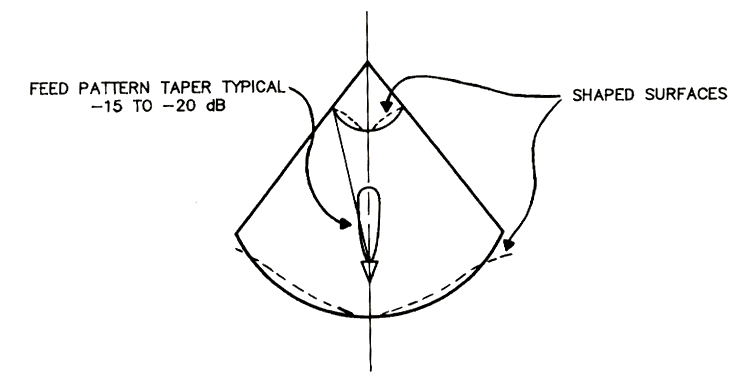
    Illumination Taper Efficiency
    We could certainly avoid spillover in the above consideration by under-illuminating the dish so that there is no chance that the radiation will miss the edge and go into the sky or ground.  However, underilluminating the dish means that some of the collecting area goes unused (in receive mode, the feed does not accept radiation from the edges of the underilluminated dish).  This is a loss of efficiency that is reflected in the illumination taper efficiency factor.  The goal is to evenly illuminate the dish all the way to the edge (uniform illumination).  To give an idea of the magnitude of the effect, for a prime focus antenna with ~ 10 dB taper at the edge, we have 0.7 < ηt < 0.8.  The shaped surfaces, above, are used to provide uniform illumination, but note that this requires use of two surfaces, properly shaped, so can only be used for cassegrain type antennas.  One can get close to unity in this factor with the use of shaped surfaces.

    Example of VLA performance:
     

    λ
    ηsf
    ηbl
    ηs
    ηt
    ηdiff
    ηmisc
    ηtot
    ηmeas
    20 cm
    1.0
    0.85
    0.82
    0.98
    0.86
    0.94
    0.55
    0.51
    6 cm
    0.97
    0.85
    0.92
    0.98
    0.96
    0.94
    0.67
    0.65
    2 cm
    0.85
    0.85
    0.90
    0.95
    0.98
    0.94
    0.57
    0.52
    1.3 cm
    0.68
    0.85
    0.90
    0.95
    0.99
    0.94
    0.46
    0.43

    The important lesson is that even though the losses for any single term seem small, the cumulative effect is that the dishes act as if they were only about 1/2 or less of their actual, physical area.  So the overall efficiency is difficult to keep near unity!

    For pointing accuracy and polarization issues, see Napier lecture.