Microflow Control Laboratory

Our group is working on a range of problems in the area of non-Newtonian and multiphase flows, and their manipulation using electric fields. The following are three representative examples of our current work:

Sudden spreading and self assembly of particles on liquid surfaces

The focus of this work is on understanding of the physics behind spontaneous dispersion of particles when they come in contact with a fluid-fluid interface (see figure). We have recently shown: (i) that this can cause particles sprinkled over a small area to spread almost instantaneously over an area that is several orders of magnitudes larger; (ii) a dropped particle causes particles already trapped on the interface to move away, creating a particle-free region around a newly-adsorbed particle; and (iii) influence the nature of monolayer clusters, e.g., porosity, on interfaces that are formed.

These phenomena have importance in a wide range of applications, such as pollination in hydrophilous plants, flotation and spreading of viruses and nanoparticles, self-assembly of micron- to nano-sized particles leading to the formation of novel nano-structured materials, stabilization of emulsions, etc. While the focus of the past studies has been on understanding the mechanisms by which particles already trapped on fluid-fluid interfaces interact leading to their self assembly into monolayered patterns, the sudden dispersion of particles coming into contact with a fluid-fluid interface which will be investigated in the proposed study has not been previously considered. These particles eventually come back together to form monolayers under the action of lateral capillary forces. We are developing techniques where an electric field normal to the surface is applied to control the process of self assembly and thus form virtually defect free monolayers (see figure).

t = 0.033 s                                t = 0.363 s

Figure. Sudden dispersion of sand particles sprinkled onto water in a Petri dish. Notice the streak lines formed due to the radially-outward motion of the particles emanating from the location where they were sprinkled.

       (a) 5000 volts                   (b) 0 volt (after using E)    

Figure. Assembly of glass particles floating at an air-oil interface. The average radius of particles is 40.5 mm. (a) When a voltage of 5000 V is applied, particles move away from each other to form a lattice whose spacing is adjustable; (b) The voltage is slowly decreased to 0 volt. The lattice remains and is virtually defect free.

Fluid dynamics of bubbles rising in viscoelastic liquids

A bubble released from rest in a liquid accelerates and, as its velocity increases, deforms because of the stresses acting on its surface. The shape of the deformed bubble after it reaches a steady velocity depends on many factors, including its volume which, together with the properties of the ambient liquid, determines the rise velocity. In a Newtonian liquid, at large Reynolds numbers (attained when the bubble volume is relatively large), the bubble assumes a mushroom-like shape. In a viscoelastic liquid, on the other hand, a small bubble remains approximately spherical, but as the bubble volume is increased it deforms into a prolate shape. Furthermore, there is a critical volume above which the bubble develops a cusp-shaped trailing end due to the extensional nature of the viscoelastic stresses in the region near the trailing end. Another interesting feature lies in the fact that the flow pattern in the wake of a bubble rising in a viscoelastic liquid is quite different from that in a Newtonian liquid. Specifically, in the former case for certain parameter values, there is an additional vortex ring in the surrounding flow corresponding to the existence of a negative wake. This, in a way, is similar to the case of a jet engine where the thrust in the forward direction is generated by ejecting gases at a fast speed in the reverse direction (Newton’s third law); the difference being that in the present study the negative wake arises simply due to the viscoelasticity of the fluid. We are using simulations and direct numerical simulations to understand this process.

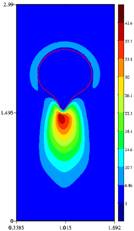
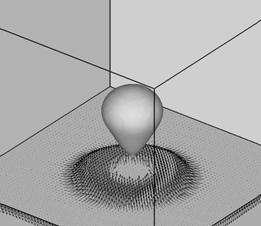
Figure. The trace of the configuration tensor A around a rising bubble, trA, from direct numerical simulations, showing that the trace is maximum at the trailing end of the bubble (left illustration). Also notice that the trailing end of the bubble is cup-shaped and the wake is negative as the velocity vectors in the wake point away from the bubble (right illustration).

Modeling of Blood flow in the human brain

The goal of this work is to determine and quantify the role played by the non-Newtonian nature of blood, i.e., shear thinning and viscoelasticity, in determining the flow rate to certain regions of the brain. This is important because under normal conditions, cerebral blood flow (CBF) is autoregulated to maintain baseline levels of flow and oxygen to the brain. However, in a patient suffering from heart failure (HF), the pressure in afferent vessels falls below the normal range within which the regulatory mechanisms can ensure a constant value for the cerebral flow rate, leading to impaired cerebration. We are developing mathematical models of CBF under normal and heart-failure conditions, and use direct numerical simulations (DNS) in conjunction with experimental data to determine how to effectively regulate CBF under normal and disease conditions.