Week 9: Confidence Interval
Section 7.1-7.2
Estimation
Given a set of data, we would like to draw conclusions about the underlying population from which the data were taken. For instance, what is the mean of the population? What is its variance?
A statistic
is a function of a random sample of observations from a population. If
we compute the value of a statistic from the data in order to provide an idea
about a particular parameter of the population, we are estimating the
parameter. The statistic is then called an estimator. If the statistic
is a single value, it is a point estimator. If it provides a range
of values, it is an interval estimator.
Confidence Intervals for μ, the mean of a population, when n is large or sample is Normal
Based on data collected about the lifetimes of GE-75 watt light bulbs, you want to make a statement such as “I am 95% confident that the average life time of GE 75-watt light bulbs is somewhere between 200 and 220 hours.” The interval (200,220) is termed a 95% confidence interval. How can you come up with a reasonable interval estimate of μ? By reasonable, I mean that you have confidence in the method used to obtain the interval. For instance, if you have to come up with an interval estimate of μ every month for your company (which buys thousands of cases of light bulbs each year), can you be assured that the intervals you provide will contain the true mean lifetime about 95% of the time?
Suppose you plan to measure the lifetimes of n GE 75-watt
light bulbs and decide to use the following (random) interval as your estimate:
,
where, 
the standard deviation
in lifetimes, is assumed to be known and n is relatively large.
Depending on the data collected, the computed endpoints of the interval will
vary. But the Central Limit Theorem
tells us that 
if our sample size is
large (When n is small, we must assume our population is
In general, a
reliable two-sided interval estimate of μ is
formed as 
.. For a
particular sample of data, the observed sample average,
is substituted for μ.
We can also form one-sided interval estimates of μ.
For instance, if we want to place an upper bound on the value of μ,
our interval estimate would be
.
(Note: For large n, an approximate
confidence interval can be formed even when
is not known, but is
replaced by its estimate, s, the sample
standard deviation.)
We can compute the number of samples necessary to obtain
an interval of a desired length L that is
with 
reliability, using the following formula: 
The length, L, can be thought of as specifying the precision of our estimate. There is an inverse relationship between the reliability of our estimate and its precision. To make L smaller while keeping the same level of reliability, n must be larger (more information is needed). For fixed L, the larger the confidence level, the larger n must be. For fixed L and reliability, the larger σ the larger n must be.
What if n is small? Then we need more information
about the population, specifically we must assume that it is
Confidence Intervals for p, the proportion of items in a population having a specified characteristic
Since the Central Limit Theorem applies to sample
proportions, analysis similar to that above tells us that a reliable confidence
interval for p can be formed as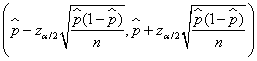
.
We can compute the number of samples necessary to obtain
an interval of a desired length L that is 
reliable using the following formula:
is a guess of p. If you have no knowledge of p
beforehand, assuming p=0.5 gives a maximum value of n over entire
range of possible values of p.