Math 662- Final Exam Name:__________________
December 18, 2000 Student #: ________________
Must
show all work for full credit!!!
I pledge that I have not violated the NJIT code of honor____________________________
1. Let X be the random variable
with exponential density f (x) = exp {-x}, x > 0,
and f (x) = 0,
elsewhere.
(a) Find the density of Y = X5 - 10.
(10 pts)
(b) Let X1, X2, …, X10
be a random sample for
m this exponential density.
Find the density of Y1 = minimum {X1,
X2,
…, X10}.
(10
pts)
2. Let X1 and X2 have the joint probability
density function given by h (x1, x2) =
2exp{-x1 - x2}, 0 < x1 < x2, zero elsewhere.
(a)
Find
the joint probability density function of Y1 = X2 and Y2 = X2 - X1.
(12 pts)
(b)
Compute E(X2 | X1).
(10
pts)
3. Let X be uniformly distributed on the interval
(-2, 3). Compute the probability density function of Y = 1 - X2.
(10pts)
4. It is discovered that 85 percent of
the pages of a certain book contains no errors.
If we assume that the number of
errors per page follows a Poisson distribution,
find the percentage of pages that
have exactly one error?
(10 pts)
5. Let X1,
X2, …,X5 be a random sample from Normal with mean 0 and variance 
.
Find the constant c so that 
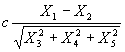has t-distribution. How many
degrees of freedom are associated with this t-distribution? Give the reasoning
behind your answer.
(12 pts)
6.
Given
below is the cumulative distribution function of the random variable
F(x) =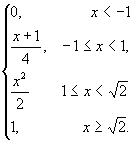 
(i) Compute P (X > 0.5 | -1 < X < 1).
(6
pts)
(ii) Compute E (X).
(10
pts)
7. Let X and Y have the joint probability
density function given by
f (x, y) = 
, y = 0, 1, 2, …; x =
0, 1,…, y, zero elsewhere.
(a) Compute E(XY).
(10 pts)