The Mystery of Dark Matter

Do the dark matter tutorial to find out how we determine the existence and distribution of dark matter in galaxies.  You will learn that the orbital speed of an object around a central mass depends on

• its distance from the central mass, and
• the total mass enclosed within its orbit.

For objects orbiting a concentrated mass (e.g. the planets orbiting the Sun), the orbital speed goes down as we go outward from the Sun because the distance is increasing, but the total mass enclosed (essentially the Sun's mass) is constant.

In the case of a galaxy, the total mass enclosed grows with distance, because more of the galaxy's mass is inside the orbit, and this trend continues until we go outside the galaxy.  For objects outside of a galaxy, we would expect the orbital speed to drop with distance, just as it does for planets in the solar system.

We can use the measured orbital speeds to "weigh" the amount of mass in galaxies as a function of radius.  When we do this, we find the surprising result that even though the visible emission (either starlight or radio emission from hydrogen clouds) is falling off at the edge of galaxies, the orbital speeds keep steady or even goes up, indicating that the enclosed mass keeps increasing.  Here is the rotation curve for our galaxy:

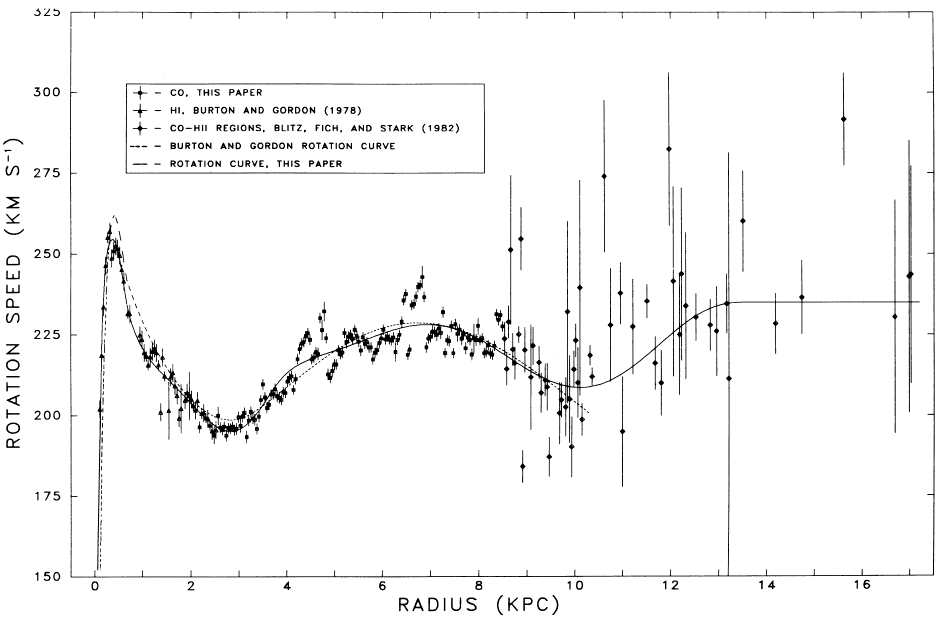
The rotation curve of the Milky Way Galaxy.  The IAU standard values of R_o = 8.5 kpc and Q_o = 220 km/s have been assumed.
(Figure reproduced from Clemens (1985), Ap. J. 295, 422.

You can see from the above figure that the central part of the galaxy contains a lot of mass in the central bulge, and as we go away from the bulge the orbital speeds go down about as we would expect.  This is shown by the plot below.  If we model a disk distribution, that can explain part of the increase in orbital speeds at around 6 kpc, but not all of it.  And as we go farther out from the center, the discrepancy keeps growing.  This "missing mass" is called the dark matter halo.

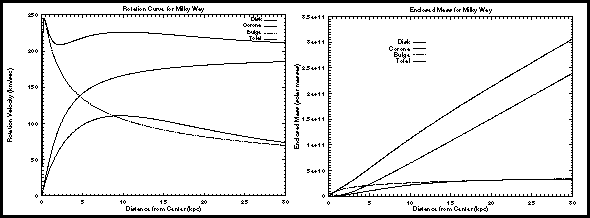
The plot on the left shows the Total rotation curve for our galaxy, made up of contributions from the Bulge, the Disk, and the Corona.  The plot on the right shows the Interior Mass, M(R), as a function of radius (called the enclosed mass here).  Both the disk and the bulge reach a constant interior mass, meaning that at a radius of 25 kpc or so, all of the mass is inside this radius, and the rotation curve for these components drops approximately as R^-1/2.  The corona mass (dark matter), however, appears to continue to rise with radius!  (This image is from Nick Strobel's web site.)
 

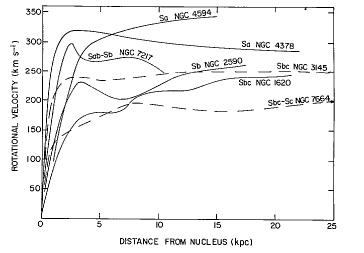
A series of rotation curves for spiral galaxies. (Figure from Rubin, Ford, and Thonnard (1978), Ap. J. Lett., 225, L107.)

Is it just our galaxy that shows this peculiarity?  The plot above shows that other spiral galaxies also show the same basic pattern -- it appears that all galaxies have dark matter halos.  If we do the same measurement with elliptical galaxies, we see the same effect.

The discrepancy is characterized by the mass-to-light ratio.  We can easily measure the total visible luminosity of a galaxy, and its distribution with radius.  If we give this amount in units of the solar luminosity L_sun, for example, we find that our galaxy has a luminosity of about 100 billion L_sun.  This is why we have claimed up to now that the Milky Way galaxy contains 100 billion stars.  If we assume that 1 solar mass creates 1 solar luminosity, then 100 billion solar luminosities would be created by 100 billion solar masses, so we would expect that the mass-to-light ratio of the galaxy would be about 100 billion M_sun / 100 billion L_sun = 1 M_sun / L_sun.  Instead, we routinely find that the mass-to-light ratio is more like 10 M_sun / L_sun, so 90% of our galaxy's mass must not be luminous -- i.e. is in the form of dark matter.

As if the situation with individual galaxies was not bad enough, we have two other kinds of evidence that the problem gets even worse on the scale of clusters of galaxies.  Recall that last time we mentioned that galaxies occur in clusters like the one below.

In these clusters we can measure the speeds of the individual galaxies, which gives one estimate of the mass to light ration. And we can measure the gravitational lensing (bending of light by the gravity of the cluster), which creates the arcs of light seen in the above picture, and gives an independent estimate of the mass to light ratio.

Speeds of Galaxies in Clusters
In the 1930's, an astronomer named Fritz Zwicky measured the dispersion of speeds of galaxies in clusters by measuring their doppler shifts.  Most or all of the galaxies will be redshifted, of course, due to the recession speed of the entire cluster, but some will be more redshifted and others less redshifted.  The dispersion of speeds means the amount of variation in these redshifted speeds, which is a measure of the random motions of the galaxies.  Assuming that the galaxies in clusters are gravitationally bound (that is, they are stably orbiting their common center of mass, and not flying away from each other) then their orbital motions will appear random, but must be less than some value (basically their escape speed).  Any galaxy in the cluster that is moving too fast will not be bound, and will fly away into space.  But how fast is too fast?  It depends on the total mass of the cluster.  The higher the mass, the higher the velocities of bound galaxies are allowed to be.

To turn the argument around, the maximum speed of the galaxies gives a measure of the total mass of the cluster.  Again, we can measure the total luminosity of the cluster and compare it to the total mass of the cluster inferred from the dispersion of speeds, and again we find that there is far more mass than would be indicated by the luminosity.  In fact the mass-to-light ratios of clusters generally exceed 100 M_sun / L_sun.

Gravitational Lensing
Both the orbital velocity of stars and gas in galaxies and the dispersion of speeds in clusters relies on Newton's Laws.  There is another way to determine the mass in clusters of galaxies using Einstein's General Relativity, which is completely independent of orbital motions.  As we noted before, light is bent when it passes near a large mass, and the higher the mass the greater the bending of the light.  A lens you can play with.  We can use this bending to determine the mass of the cluster as follows:

• find multiple images of a single galaxy created by the gravitational lensing (the bluish features in the above picture). (How do we know they are multiple images of a single galaxy?)
• determine the angular distance to the multiple images as seen in the picture.
• determine the distance to the distorted galaxy from its recession velocity and Hubble's Law
• determine the distance to the cluster in the same way, using Hubble's Law
• use Einstein's theory of general relativity to relate the angular separation to the mass of the cluster.

When this is done carefully, we find exactly the same result as before -- the universe contains as much as 10-100 times more dark matter than ordinary luminous matter!

Dark matter is mysterious, but it need not be exotic.  One possibility is that it is simply small but dense objects of ordinary matter that are invisible.  Examples are brown dwarfs (too small to be stars, and too faint to detect in the galactic halo), black dwarfs (old white dwarfs that have cooled off and no longer emit much light), black holes, or perhaps some other form of ordinary matter.  Such matter is called baryonic matter, because it is made up of baryons (protons and neutrons).  Astronomers have whimsically termed such objects as MACHOs (MAssive Compact Halo Objects).  Since such objects are too faint to see, we have to use other means to detect them.  One way is to look for tiny gravitational lensing events as they pass in front of distance light sources.  In fact, such tiny lensing events have been seen, but not in the huge numbers that would be required to account for the missing matter.

A more exotic possibility is that the dark matter is not in the form of ordinary matter, but rather is made of some kind of sub-atomic particle that we have not yet discovered.  Such particles would have to have lots of mass, but not interact with light.  Astronomers have (again whimsically) termed such objects as WIMPs (Weakly Interacting Massive Particles).  We have already met one kind of weakly interacting particle -- the neutrino.  But neutrinos, which do exist in huge numbers, have two problems.  One is that they do not have enough mass (although they may contribute a small amount to dark matter outside galaxies), and the other is that they would not collect around galaxy clusters.  They are so energetic that they zoom around the universe anywhere they want to go, and barely feel the mass centers in clusters of galaxies.  Instead, we need some kind of particle that is more massive than neutrinos, and that is slower so that it can collect around mass centers.  So far we have not discovered such particles, but perhaps someday particle experiments will identify them.

Meanwhile, we are stuck with no certain explanation, and not too many clues.  One important clue that seems to favor WIMPs over MACHOs is the distribution of the dark matter.  Ordinary baryonic matter has collected in the centers of mass concentrations like galaxies and clusters of galaxies, so whatever dark matter is, it must resist clumping on these scales.  WIMPs fill this expectation nicely, since they would have been born rather hot (high speed) in the Big Bang.  Baryons were also hot, but they interact with light and so produce radiation that allows them to shed their energy, cool, and collect into galaxies, etc.  WIMPs, on the other hand, have no way to lose energy, so they would remain more loosely clustered in galaxy halos.

In the very first lecture we discussed the fact that our galaxy is part of the Local Group of galaxies, comprising the Milky Way Galaxy, the Andromeda Galaxy, the Magellanic Clouds, and some 20 others.  We also said that the Local Group was part of a larger collection of galaxies called the Local Supercluster.  As we look out into the night sky, we see huge numbers of galaxies in all directions, and from their recession velocities and Hubble's Law we can determine their distance.  From this we can build up a 3-dimensional map of galaxy locations.  What we find is that galaxies are not uniformly distributed in space, but rather form these huge structures called superclusters, held together by gravity.

By measuring the peculiar velocities of galaxies (their velocities after subtracting their recessional velocity), we find that they seem to be gathering into concentrations of mass.  Here is Figure 21.13 from the text The Cosmic Perspective, which plots the peculiar velocities of galaxies near ours (the Milky Way Galaxy is in the center).

Fig 21.13 from the Cosmic Perspective, by Bennet, Donahue, Schneider & Voit, Addison Wesley (1998)

The galaxies appear to be moving "downhill" into several concentrations of mass.  When we look farther out into the universe, the large scale structure of the universe becomes apparent.  There are regions of superclusters, and other regions called voids, which contain no galaxies at all.  The overall structure appears like a sponge, with spherical voids separated by membranes of mass.

Fig 21.14a
Fig 21.14b
Fig 21.16a Looking into the past.

To explore how this structure was created, we can start with the Big Bang and imagine some tiny fluctuations in the early universe.  These fluctuations would have been slightly cooler, and allowed mass to collect and collapse, which further cooled the region (by radiating excess energy away), so that the areas where matter collects gets more concentrated.  So the large scale structure that we see shows us what the early universe must have been like.  We can run simulations and see what initial conditions are needed to make the universe appear as it does today.

The fate of the universe is tied up in this question.  Will the universe continue to expand forever, or will it eventually stop expanding and start to collapse (to end in the "Big Crunch," which is the opposite of the Big Bang)?  The answer to this question depends on the density of the universe.  There is a critical density at which the universe will slow down but not stop expanding -- just balancing on the edge between expanding forever and collapsing.  If the universe is less than the critical density, then it will continue to expand forever (leading to an open universe), while if it is more that the critical density it will eventually stop expanding (leading to a closed universe).  At exactly the critical density, the universe will keep expanding forever, but will go more and more slowly so that it eventually would stop after an infinite time has passed.  This is called a flat universe.

Note that each of these scenarios indicates that the expansion should be slowing down, even if it never comes to a stop.  When we do measurements designed to determine whether our universe is open or closed, it always seems to indicate that we are very very close to a flat universe.  That means that our universe is close to the critical density.  Yet, when we count up all of the matter, we find that it is not enough to make the universe flat, even if we include dark matter.  In fact, if we call the critical density r_crit, then the matter density appears to be around 0.3 r_crit.  Yet we should be able to tell if the universe were so open (so far below the critical density), and our observations do not show it.  For many years we have had this apparent contradiction -- the universe appears to be flat, but there is too little matter (including dark matter) to make it so.

Recently, things have gotten even stranger.  By measuring the most distant supernovae, which we believe to be standard candles, it appears that the universe was once expanding more slowly that it does now.  In other words, the rate of expansion appears to be accelerating!  Astronomers are now toying with the idea that there is an exotic form of energy that is pushing space apart -- a kind of negative gravity.  This form of energy is called dark energy, and it is possible that, if there is enough dark energy, it might explain why the universe appears flat.

Next time (our last lecture) we will look into the question of cosmology, the Big Bang and the beginning of the universe.