When Tycho lay on his deathbed,
he begged is protege, Johannes Kepler (1571-1630) to take his careful measurements
of the positions of the planets and prove that the Tychonic theory was correct.
However, Kepler was a proponent of the Copernican theory, and he was a careful
mathematician who simply wanted to discover the true laws of planetary motion.
With Tycho's measurements, Kepler tried to fit a number of different curves
to the positions of the planets.
To get a flavor for how he did
this in the case of Mercury, he took the measurements of Mercury's greatest
elongation, as shown in the following movie (made for elongations in 2001
and 2002) and determined the location of the planet relative to the Sun and
Earth. The path of multiple elongations maps out a curve, which he tried to
fit.
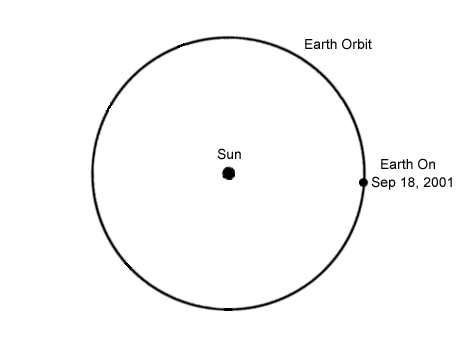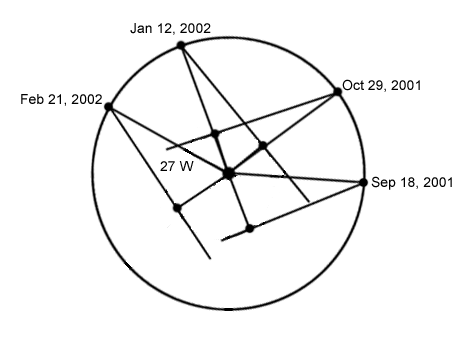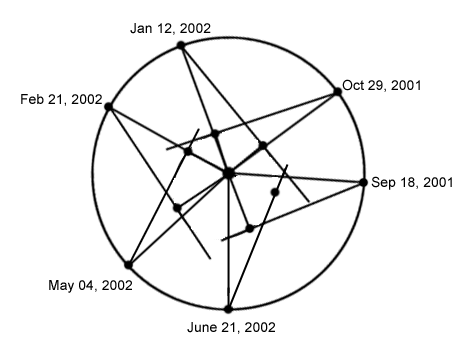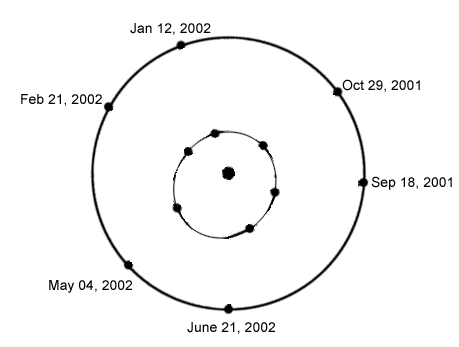
He tried fitting circles, with
centers offset from the Sun as needed to fit the points, but Tycho's measurements
were much too precise to allow such a solution. He tried ovals and other curves
of various kinds, and only after many long years of checking and rechecking his
numbers did he come up with his famous three laws of planetary motion:
- Kepler's 1st Law:
Planets orbit the
Sun in ellipses with the Sun at one focus.
- Kepler's
2nd Law: An
imaginary line from the Sun to the planet sweeps out equal areas in equal
times.
- Kepler's
3rd Law: The
square of a planet's orbital period is proportional to the cube of the orbit's
semi-major axis (or P2
= ka3).
Let's examine these a bit more, and
look at some implications:
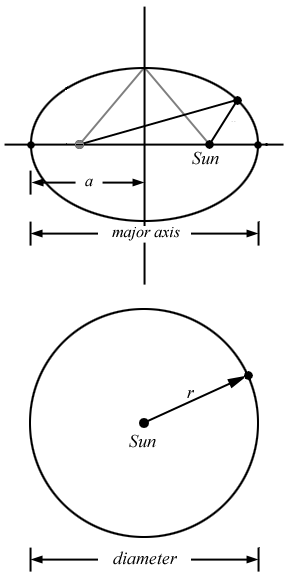 |
Kepler's 1st
Law: An ellipse has
a long axis (called the major axis). It also has two foci (focuses).
One focus is where the Sun is located, the other focus is empty. As
the two foci are brought together, the ellipse looks more and more
like a circle. In fact, a circle is just a special case of an ellipse
with the two foci at the same place (the center of the circle), in
which case the major axis is the diameter of the circle. Half the
major axis is called the semi-major axis (a
in the upper figure, r
in the lower figure).
Kepler's
2nd Law: Combined with
the first law, this law states how
fast a given planet moves in its orbit. A planet moves faster
when it is near the Sun (perihelion), and slower when it is farther
from the Sun (aphelion). But it says that in a very quantitative way.
Kepler's
3rd Law: This law states
how one planet's speed (or period) relates to another. The two planet
orbits on the left have the same period, because they have the same
semi-major axis.
|
It is important to realize that
the 2nd and 3rd laws are quantitative, meaning that one can calculate the
actual distances (semi-major axes) and speeds, etc., using them. For the case
of planets going around the Sun, for example, with P
in years and a in
Astronomical Units (AU), the third law
becomes just: P2
= a3. This is trivial for
Earth -- P = 1 year
and semi-major axis a
= 1 AU, but we can also measure the period of Venus (P
= 0.615 years), and get its distance from the Sun (a
= 0.723 AU). We will see later what the constant k
is in the formula P2
= ka3, so that Kepler's 3rd
law can be extended to other orbits, such as the Moon around the Earth.
Lecture Question
#1
Kepler's Laws allow us to construct
a scale model of the solar system, knowing the exact shapes and relative sizes
of the planetary orbits. But it does not allow us to determine the absolute
size of any orbit. All the distances are relative to the Astronomical Unit
(distance of the Earth from the Sun). In fact, the actual distance to the
Sun was not known until a transit
of Venus in 1761 offered a chance to get an accurate triangulation. Nowadays
we can measure planetary distances very accurately using radar signals.
 |
|
Venus crossing the disk of the Sun on 2004 Jun 08
(photo taken by Dale Gary) |
Venus just touching the limb of the Sun on 2004 Jun 08
(photo taken by Dale Gary) |
Isaac Newton (1642-1727) took
the ideas of Kepler and Galileo, and put them together into three Laws of
Motion and the Universal Law of Gravitation. These laws, plus a little calculus,
are sufficient to explain and quantify virtually all mechanical phenomena
we see on Earth and throughout the universe. Newton's 1st law, the law of
inertia, states that something in motion will continue to move at the same
speed in a straight line unless acted on by an outside force. This was a key
realization, also noted by Galileo, that finally could account for the motions
of planets. One of the big questions had been, what keeps the planets moving
forever in their orbits. The answer is inertia -- they are
moving so they keep moving. But they are
NOT moving in a straight line, and Newton realized that that must mean there
is a force acting on them. But what was this force, and how could it work
at such a distance?
Lecture Question
#2
Another help was his 2nd law, which
quantifies the relationship between force and acceleration and introduces
the concept of mass. He determined that a body of half the weight would be
accelerated twice as much by a given force, i.e. force equals mass x acceleration:
F = ma. But equally
important was his 3rd law, which states that for every force there is an equal
and opposite reaction force. That means that when a falling object, say a
stone or an apple, is accelerated toward the Earth due to the force of gravity
by the Earth, the object also exerts exactly the same force on the Earth (so
the Earth is accelerated toward the object, albeit by an imperceptible amount).
He noted that falling objects accelerate
with constant acceleration toward the center of the Earth, and postulated
that the Moon is also doing the same -- that is, the Moon is continually falling.
It is only the side-ways motion of the Moon that keeps it from hitting the
Earth. But to check that idea, he had to know quantitatively what the magnitude
of the force should be at the distance to the Moon. He knew it should become
smaller, but exactly how?
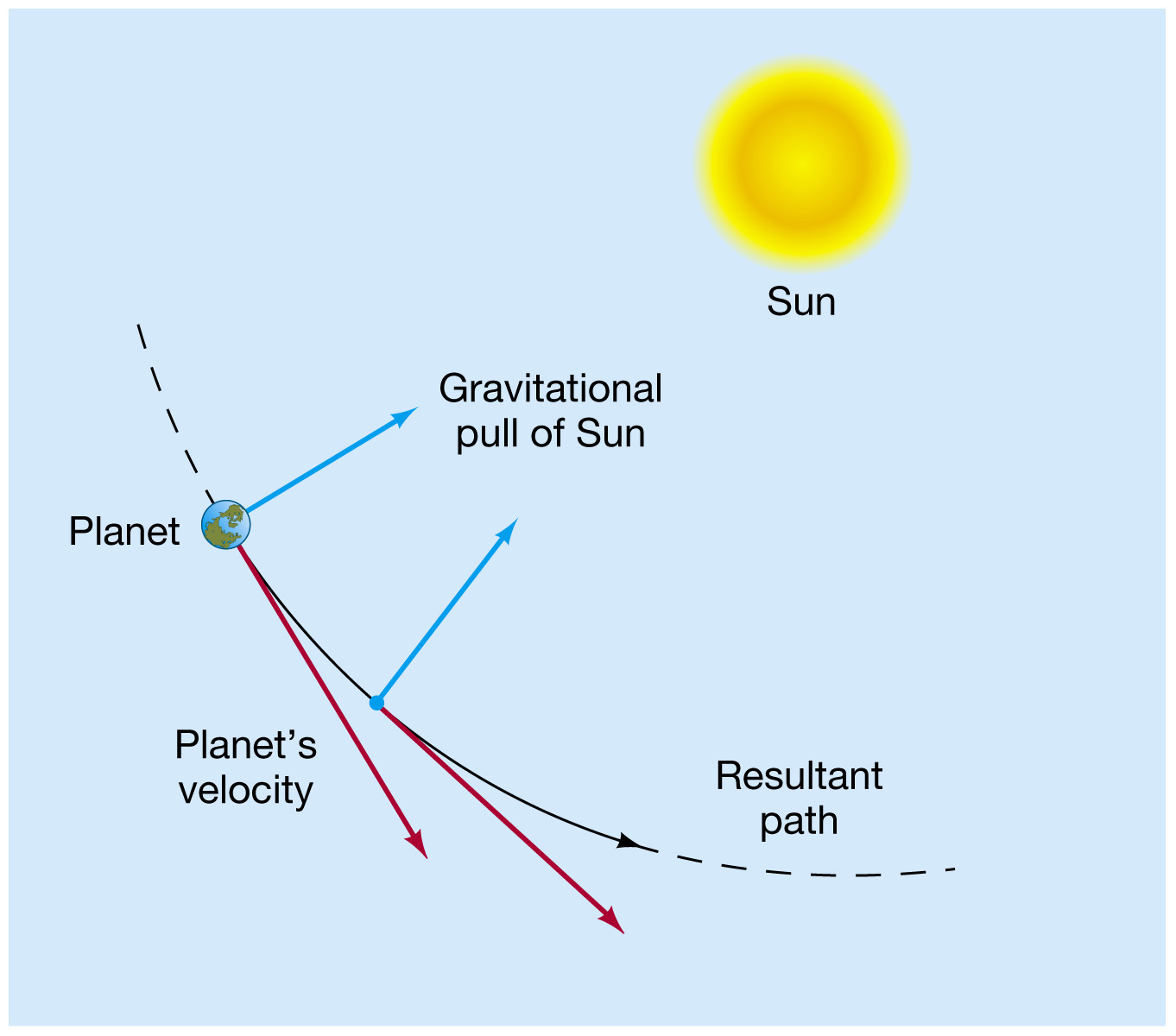 |
The Sun's inward pull of gravity on a planet competes with the planet's tendency to continue moving in a straight line. These two effects combine, causing the planet to move smoothly along an intermediate path, which continuously "falls around" the Sun. This unending tug-of-war between the Sun's gravity and the planet's inertia results in a stable orbit. (Fig. 1.24, Chaisson & McMillan, Copyright Prentice Hall, 2004) |
So Newton basically guessed
that the fall-off in the force should go as the square of the distance (a
so-called inverse-square-law), and by
his third law the force between the Earth and the Moon should be proportional
to the product of the masses. Using this guess, he calculated how far the
Moon would fall in 1 second, and using his knowledge of the distance to the
Moon and the period of the Moon's orbit, he found that the amount agreed exactly
with his law. This was the Universal Law of Gravitation
(F = - GMm/r2),
which states that the force between two masses is proportional to the product
of the masses and inversely proportional to the square of the distance between
them. G
is called the gravitational constant. The Universal Law of Gravitation is
the reason things fall to Earth, and it is also the reason the Moon circles
the Earth and the planets circle the Sun.
It turns out that using Newton's Laws
and some other laws of physics it is possible to theoretically understand
all of Kepler's laws. In particular, the constant k
can now be given as k
= 4p2/[G(M+m)],
where M
is the mass of the more massive body and m
is the mass of the less massive body. This allows us to use the law for any
two orbiting bodies. Without it, we could not send a spacecraft to Mars, or
predict the orbit of the Space Shuttle around Earth. The overall equation
for Kepler's third law is:
P2
= (4p2/[G(M+m)]) a3.



