Differential Gravitational Forces

There is a general process that is responsible for each of the following phenomena:

• Rings of Saturn 
• Volcanoes of Io 
• Earth ocean tides
• The Moon keeping the same face toward Earth
• The breakup of the comet Shoemaker-Levy 9 that crashed into Jupiter  and crater chain on Ganymede.
• The resonance between Saturn's moons, Titan and Hyperion
• Accretion disks around black holes

The basic process is differential gravitational forces, which means gravitational forces that are not equal across the finite size of a body.  It may seem that on Earth we should feel the same gravitational force from the Sun anywhere on Earth, but in fact we are 13,000 km closer to the Sun on one side of the Earth (near noon) than when we are on the other side (near midnight).  This 13,000 km may seem a small difference in the 150 million km distance from the Sun, but even so the difference has consequences.  Let's calculate the force difference on two sides of a body of radius R, a distance d from the Sun.  We will use the example of the Earth, but the same expression will work for any body.

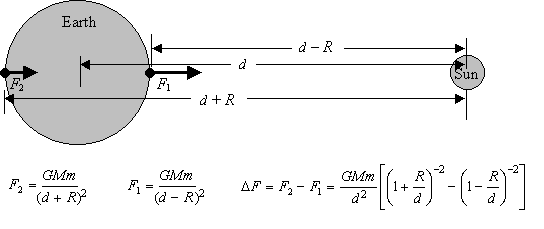
Figure 1: Forces on opposite sides of a body (in this case, the Earth) due to a distant
body (in this case, the Sun).  The force F₁ is larger than F₂ because that side of the
body is closer to the primary.  The difference in forces, DF, is as shown.  The terms in
rounded parentheses can be expanded in the small term R/d.

The gravitational force for any small element of mass m, of the body, is just

F = GMm/r².

where r is the distance between the center of the primary of mass M and the small elemental mass m.  Since the distance on the near side is r = (d -R), and the distance on the far side is r = (d + R), we get the two forces shown above.  The difference in these two forces then gives the expression

DF = F₂-F₁ = GMm/d²[(1 + R/d)^-2 - (1 - R/d)^-2].

We can expand the terms in rounded parentheses using the binomial expansion

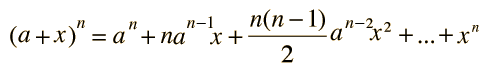
to get a final expression for the difference in force from one side of a body to the other:

DF = -4GMmR/d³,    (R is the radius of the body, d is the distance to primary).

The minus sign means that the force is less on the more distant side.  This expression is valid only for the two special points on either side of the body on the line joining the two bodies.  In the text, a more general approach is used to get an expression for anywhere within the body.  These differences in the force experienced within a body lead to tidal bulges, as shown in Figure 2, below.
 
 

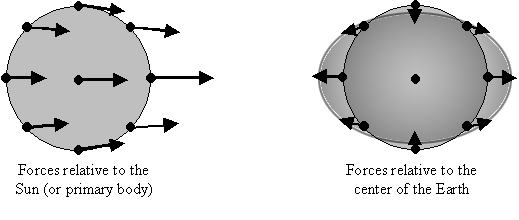
Figure 2:  Differential (tidal) forces on a body relative to the primary (left), and relative to its
own center (right).  The forces relative to its center stretch the body along the line joining the
body and the primary, and compress the body along the perpendicular directions, to form a
football shape (prolate spheroid).

The figure on the left shows the forces relative to the Sun, and the figure on the right (obtained by subtracting the central force vector on the left from all of them) shows the forces relative to the center of the body.  These relative forces tend to stretch the body laterally, and compress the body in the perpendicular direction, to form a football shape.

Both the Moon and the Sun exert tidal forces on the Earth.  Let's calculate the relative magnitudes of those tidal forces.  We will call the force due to the Moon DF_Moon, and the force from the Sun DF_Sun.  The ratio is not going to depend on R, the radius of the Earth, or on m, the mass element within the Earth, but will depend on M, the mass of the primary, since it is a different primary in the two cases.  The ratio is:

DF_Sun/DF_Moon = (M_Sun/M_Moon)(d_Moon/d_Sun)³
                     = (1.99x10³⁰/7.36x10²²) (3.84x10⁵/1.50x10⁸)³
                    = 5/11.

So the Moon exerts more than twice the influence as the Sun, but the Sun's tides are still significant.

Because the oceans, being liquid, are easily deformable, the most obvious response to these tidal forces is the ocean tides.  As the Earth rotates, the continents pass through these tidal bulges once a day, causing the diurnal tides every 12 hours.  When the Sun and the Moon line up (near new or full Moon), the forces add together and cause very high spring tides (the word spring is not related to the season!).  When the Sun is 90 degrees from the Moon (near first and third quarter), the high and low tides are not as great--these are called neap tides.

Questions (click here for answers):

• What time of year should the very highest tides occur?
• During some years, this highest tide is higher than others.  Why?

The ocean tides are not the only effect of these tidal forces.  The solid body of the Earth also bulges slightly in this way.  The daily flexing of the Earth (both solid body and sloshing of the oceans) cause loss of energy of the Earth's rotation, due to friction.  This energy goes into heat, increasing the Earth's internal temperature.  The loss of rotational energy means that the Earth is slowing down in its rotation rate, currently by about 0.002 seconds per century.

As you might imagine, the Earth also exerts tidal forces on the Moon.  In fact, the tidal forces of Earth on the Moon are about M_EarthR_Moon/M_MoonR_Earth ~ 20 times larger than those from the Moon on the Earth.  Note what happens when a rotating body is tidally distorted.  The line of distortion is continually being rotated away from the line between the two bodies, causing the bulges to lead slightly.  There is then a net torque opposing the direction of rotation, thus slowing down both bodies.  This torque exists until the slowing rotation causes the body's orbital period to equal its rotational period.  Once this happens, the body is said to be tidally locked, and the torque and dissipation by tidal forces ceases.  At this moment in time, the Moon is tidally locked with the Earth, but the Earth is not tidally locked with the Moon.  That is why the Moon keeps the same face to the Earth.  In the distant future, the slowing Earth will eventually become tidally locked with the Moon, and no further evolution of the system will occur.

When this occurs, what will the Earth/Moon system look like?  It is interesting to note that the leading bulge of the Earth also exerts an extra pull on the Moon in its orbit, giving a slight acceleration along the orbit, and therefore an increase to its orbital velocity, v_q.  This means the Moon's orbital angular momentum L = mrv_qincreases with time.  In a beautiful confirmation of the law of conservation of angular momentum, we know that this has to come from somewhere else in the system.  In fact, the rotational angular momentum lost by the Earth through this tidal interaction is exactly the orbital angular momentum gained by the Moon!

Do we expect the Moon then to come closer to Earth, or move farther away?  We can answer this by comparing velocities in different orbits given by Kepler's third law (for a circular orbit), P² = kr³.  The period is related to the orbital velocity and circumference of the orbit by v = 2pr/P = 2pr/kr^3/2 ~ r^-1/2, so the angular momentum is proportional to vr ~ r^1/2.  So larger orbits have larger angular momentum, despite the fact that their orbital velocity is lower.  It may seem paradoxical that by increasing the orbital speed of a body, its orbital radius increases and its orbital speed ends up getting smaller, but that is the way of things!

The complete picture is as follows:

• The tidal forces of Earth on the Moon slow down the rotation of the Moon (while speeding up the rotation of the Earth).
• The Moon eventually keeps the same face toward the Earth, becoming tidally locked.
• The tidal forces of the Moon on the Earth slow down the rotation of the Earth, while speeding up the orbital motion of the Moon.
• The Moon spirals away from the Earth, increasing its angular momentum, compensating for the lost angular momentum of the Earth rotation.
• The Earth eventually keeps the same face toward the Moon, becoming tidally locked.
• At this point, the system stops evolving and remains in this configuration forever (except as influenced by external forces).

We said before that the Earth is slightly oblate because of its rotation, and the resulting centrifugal force causing a change in shape of the rotating Earth.  Because of the tilt of the Earth's rotation axis, this bulge is tilted relative to direction of forces from the Sun.  The differential force of the Sun on one side of this bulge relative to the other side is such that the Earth is being pulling in the direction to decrease the tilt angle.  Because the Earth is rotating, however, such a torque is not successful in righting the Earth, but rather causes a change in angular momentum perpendicular to the spin axis.  This torque causes the Earth to precess, just as a leaning top would.  This is just the precession we learned about in the previous lecture.  The period of precession of the Earth is 26,000 years, and causes the direction of the pole to change in the sky, as well as causing the crossing point of the ecliptic and the celestial equator to move westward by about 50" per year.

Because the Moon's orbit is tilted slightly (about 5 degrees) from the ecliptic, and of course it orbits once per roughly 28 days, the direction and magnitude of the net torque on the Earth due to the Sun and Moon changes on monthly and yearly time scales.  This causes a slight nodding of the axis on these time scales, so that the precession motion is not a smooth circle in the sky, but is a wiggly circle.  This nodding of axis is called nutation.  In the next lecture we will learn more about the Moon's orbital motion.

The differential gravity forces on a body, shown in Figure 2, stretch the body along a line between the body and the primary.  This is due to the gravity gradient, which we can see is proportional to 1/d³, where d is the distance between the bodies.  It follows that if a body approaches the primary too closely, the difference in force across the body's diameter can be greater than the forces holding the body together.  When this occurs, the body is literally torn apart.  For large bodies (R > 500 km), gravitation dominates all cohesive forces.  For smaller bodies (e.g. a comet), the tensor strength of the material making up the body provides the dominant force.

For such larger bodies, Edouard Roche showed that a satellite will be torn apart by gravitational forces if it approaches the primary closer than a distance

d = 2.44 (r_M/r_m)^1/3 R ,

where r_M is the average density of the primary (in kg/m³), r_m is the average density of the satellite, and R is the radius of the primary.  The above expression is only for larger bodies where gravitation is the dominant force holding the satellite together, but it turns out that different cases differ only by the numerical factor.  For example, for rocky bodies greater than 40 km in diameter, the coefficient is 1.38 instead of 2.44 (that is, these smaller bodies can approach somewhat nearer the primary before being torn apart).

Let's calculate the Roche Limit for an icy body (r_m ~ 1200 kg/m³) around Saturn.  From Table A3-3, the radius of Saturn is R_S = 60,000 km, and the average density of Saturn is r_M ~ 690 kg/m³, so such a body could come no closer than

d = 2.44 (690/1200)^1/3 R_S = 2.03 R_S = 122,000 km,

without being torn to bits.  Note that the rings of Saturn extend from 80,000 to 136,000 km from the center of Saturn, so either the body that was torn apart to form the rings approached within 122,000 km, or else the body was less dense than 1200 kg/m³ (e.g. if r_m = r_M, then d = 2.44 R_S = 150,000 km).  Incidentally, although the rings of Saturn cover a huge area, they are very thin, with a total mass of only 10¹⁶ kg.  A body of this mass, with a density of 1200 kg/m³ , would have a radius of only about 13 km.

====================
Answers: (Back to Questions)

• The highest tides should occur (at the time of full or new moon) near perihelion (when Earth is closest to the Sun), which currently happens around 2 January.
• Because in these years, Full or New Moon occurs with the Moon at perigee (closest to Earth), near 2 January.  This situation gives the very highest possible tides.