| Physics 320 |
Astrophysics I: Lecture #13
|
Prof. Dale E. Gary
NJIT
|
Atmosphere and Magnetosphere
of the Earth and Moon
Atmospheres
We will learn later about atmospheric structure in some detail for each of the planets. Here we just want to look at some useful relationships for atmospheres, which basically means looking at the physics of gases. We start with the ideal gas law, which gives the relationship between pressure, density, and temperature for an atmosphere:
P = nkT
where P is the pressure (force per unit area, or N/m2), n is the gas number density (particles per m3), k = 1.38 x 10-23J/K is Boltzmann's constant, and T is the gas temperature in K.
The ideal gas law is based on the idea of kinetic temperature, which describes a distribution of speeds of the gas molecules (or atoms) in terms of temperature. A hot gas has faster moving particles than a cold gas. The thermal distribution is an equilibrium distribution (called the Maxwellian distribution)
Imagine firing a beam of particles, all with the same energy, into a trap and allowing them to come into equilibrium by colliding elastically. Due to standard probability and statistics (akin to coin-tossing), they will wind up with a gaussian distribution of speeds (a bell curve). Any distribution of particles in equilibrium will have such a curve, which can be parametrized by a single number, the temperature. Due to the 3D nature of velocity, the gaussian when expressed in terms of speed becomes:
nv dv = n (m/2pkT)3/2exp(-1/2 mv2/kT )(4pv2) dv
where the important dependence is the argument of the exponential, which is just the ratio of the kinetic energy (1/2 mv2) to thermal energy (kT ). This expression is the number of particles per unit volume having speeds between v and v + dv.
Important relationships:
- Peak of distribution (most probable speed) is when 1/2 mv2 = kT, or
- Root mean square speed is somewhat higher (due to asymmetry in the curve)
Video showing Maxwellian Distribution
The way that we can use this for planetary atmospheres is to think about the speeds of the gas particles making up the atmosphere, relative to the escape speed
ve = (2GM/R)1/2
which comes from equating the kinetic energy of a projectile to its potential energy at the surface of the planet
1/2mv2 = GMm/R.
If a gas has a temperature such that vrms=ve, then the gas will leave the atmosphere in only a few days. To retain an atmosphere for several billion years (the age of the solar system is about 4.5 billion years), a planet must have
ve > 10 vrms
(the factor of 10 takes into account the high-speed tail of the Maxwellian Distribution).
The figure below shows the retention of different atmospheric constituents on different solar system bodies, according to this simple relationship.
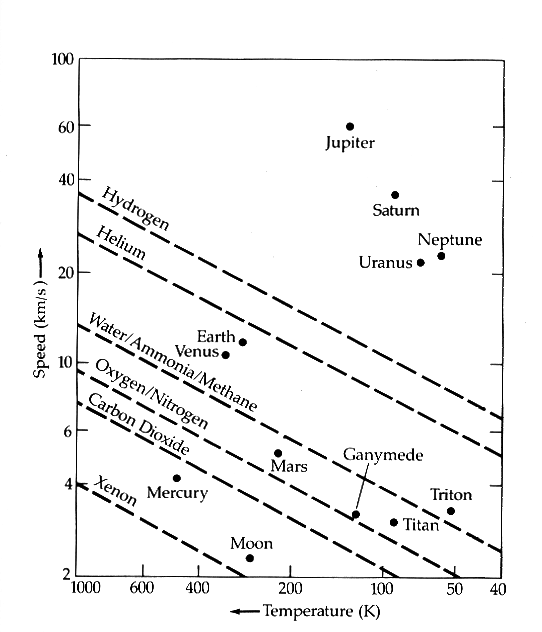
Diagonal dashed lines show the relation ve > 10 vrms for different atmospheric
constituents. The dots indicate the escape speed (vertical axis) and equilibrium
temperature (horizontal axis) for different solar system bodies. Earth's placement
indicates that it can retain Water, but not Helium or Hydrogen, over the course
of the age of the solar system. From Zeilik & Gregory, Astronomy & Astrophysics.
Moon
Does
the Moon have an atmosphere? Recall our earlier calculations that
compared the escape speed of a body (vesc
= [2GM/R]1/2)
with the speed of the gas particles (vrms
= [3kT/m]1/2)
making up its atmosphere. Unless the gas particles are moving a lot
(a factor of 10) slower than the escape speed, the particles will seep
out of the atmosphere over time. Can the Moon hang on to oxygen (02)?
We have:
vesc
= [2GM/R]1/2 = [2(6.67x10-11)(7x1022)/1.738x106]1/2=
2.32 km/s
vrms
= [3kT/m]1/2 = [3(1.38x10-23)(387)/((32)(1.66x10-27))]1/2
=
0.549 km/s
so the
escape speed is only 4.2 times the rms speed. The Moon will lose any
oxygen that might be produced, after only a few hundred years.
Any
atoms lingering around the Moon, produced due to outgassing or spalation
from rocks, lasts only for a short time and must be continually replenished.
The atmosphere of the Moon is an amazingly good vacuum, only 10-14
atm.
Earth
The
Earth's atmosphere would have started out to be mostly H and He, but lost
it due to the speed of these particles allowing them to escape over time.
A new, heavier atmosphere of H2O, O2,
N2, and CO2
was outgassed from volcanism, or brought here by comets.
We
already derived the equation of hydrostatic equilibrium, which holds for
the interior of the Earth, but also of course for the atmosphere:
dP/dr = -rg
but there
is another useful law that relates pressure and density--the Ideal Gas
Law:
P = nkT = rkT/m,
where
n
is the number density (number of particles per unit volume), related to
the mass density by n = r/m
(m
is the mass/particle). Thus, we can write r
in terms of P,
and get a new equation for P:
dP/dr = -P(mg/kT)
or
dP/P = -(mg/kT)
dr
Just exactly
as we solved the similar equation for radioactive decay, this equation
has the solution:
P = P0e-(mg/kT)h
where
h
= (r -r0)
is the height above the surface of the Earth. Thus, there is a pressure
scale
height,
H = kT/mg = constant
which expresses the distance
over which the pressure falls from its initial pressure by a factor of
1/e.
The scale height for the Earth's surface is roughly 8 km, although note
that to get this result we had to assume that the temperature T
does not change with height. This is not true for Earth's atmosphere--T
falls with height (near the surface), so that the scale height is lower.
Still, the concept of a scale height is useful for atmospheres, and next
semester we will again use it to describe the atmospheres of stars.
Atmospheric temperature structure:
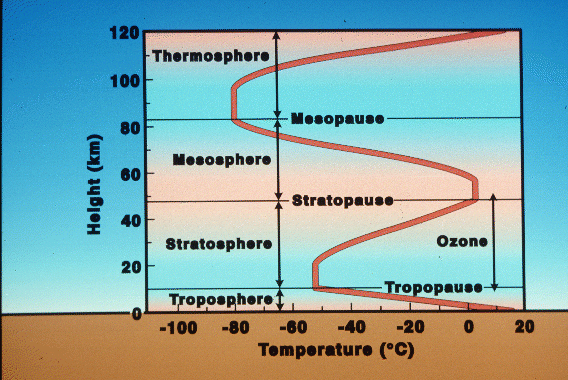
Why
does the temperature of the atmosphere drop to a height of about 10 km,
then start to rise again in the Stratosphere? This is due to absorption
of ultraviolet (UV) light from the Sun, which deposits energy in this region
of the atmosphere, and heats it. This region is called the Stratosphere,
because it is stable to upward motions (an inversion layer), which means
that clouds do not rise in columns, but spread out in thin layers, like
strata. Up to the Mesopause, the temperature again declines, but
then rises again in the Thermosphere due to absorption of X-rays from the
Sun. This "atmosphere" is only slightly below the height of low Earth
orbiting satellites such as the Space Shuttle, which orbits about 200 km
up.
Magnetic
Fields
The
rotating liquid metallic core of the Earth generates magnetic fields that,
at the surface, primarily look like a dipole (a North and South magnetic
pole), although there are higher-order multipole (quadrupole, etc.) components
as well. A dipole field falls off in strength as
B = B0(r/REarth)-3
The North
geographic pole of the Earth actually is a South magnetic pole. Why?
This means that the direction of the field lines is out of the Earth at
the South geographic pole, and into the Earth at the North geographic pole.
At the surface of the Earth, the magnetic field strength is about 0.4 gauss,
or B0= 4 x 10-5
T (tesla is the SI unit). The magnetic
fields reach far out into space, and surround the Earth in a protective
region called the magnetosphere.
Look at a real time monitoring
of the magnetosphere.
Example:
for a proton with speed v = 107
m/s, in field of B = 10-5
T the gyroradius is:
r = mv/eB = (1.67x10-27
kg)(107 m/s) / (1.60x10-19
C)(10-5 T) =
10.4 km.
This means
that such a proton will execute a circular gyration path of radius 10 km.
If it travels inward along the magnetic field toward one of the poles,
the magnetic field strength goes up, and it spirals in a smaller circle.
It will be mirrored if the field strength gets high enough, and it ends
up trapped, bouncing forever from pole to pole, and drifting around the
Earth.

