Before we begin to discuss Mercury, let us take a look at the general situation with regard to surface temperatures of planets, relative to the temperature of the central star. An important property of a planet is its albedo.  This is the fraction of sunlight reflected from the surface, relative to the amount striking the surface:

A = amount reflected / amount incident

A perfectly reflective planet would have an Albedo of 1, while a completely black planet would have an albedo of 0. Wikipedia lists the albedo of the planets, where you can see that it varies from very dark (0.11 for the Moon) to very bright (0.67 for cloud-covered Venus).  The gas giants have albedos near 0.5.  Earth's albedo is highly variable (due to clouds), but averages around 0.37. Saturn's moon Enceladus has an albedo above 1 (1.4)! Keep in mind that albedo numbers are difficult to calculate, and vary quite a bit in different references.

We can measure the amount of light reflected from a planet, but how do we know the amount striking it?  The light, of course, originates at the Sun, which radiates as a blackbody of temperature about T = 5800 K.  The blackbody spectrum peaks at a wavelength that depends only on temperature:

l_max = 2.898 x 10^-3 m/T

a relationship called Wien's Law.  The Sun's spectrum peaks around 500 nm.  The spectrum of an object at room temperature (about 290 K) peaks in the infrared (about 10 mm).  Thus, we can tell the surface temperature of a planet by measuring its blackbody spectrum.  A blackbody spectrum has a total energy flux F (energy per unit area per unit time) given by the Stefan-Boltzmann Law

F = sT ⁴ W/m²,     where s = 5.67 x 10^-8 W m^-2 K^-4.

Since we know the energy flux from the Sun, we can calculate the blackbody temperature one would expect at the surface of a planet from its distance from the Sun, and its albedo A.  It should be obvious that the energy flux from the Sun integrated over an entire sphere centered on the Sun (called the Luminosity) is the same no matter how big the sphere is. Therefore, 4pR²_sunsT ⁴_sun = 4pr²_psT ⁴_p, where r_p is the distance of the planet from the Sun, and T_p is the corresponding temperature at that distance if all of the energy were absorbed by the planet (A = 0). If some of the energy is reflected (A > 0), then the temperature of the planet will be less than this. We can take this into account by including a factor (1 - A), so the relation becomes 4pR²_sunsT ⁴_sun = 4pr²_p (1 - A) sT ⁴_p. Solving for the sub-solar temperature of the planet, we have

T_ss = 394 (1 - A)^1/4(r_p)^-1/2 K,   (r_p= distance from Sun to planet, in AU).

For a planet that rotates slowly, or has little atmosphere, the sub-solar temperature is the relevant one to use.  However, when the planet is rotating rapidly, or has a substantial atmosphere, the redistribution of energy must be taken into account.  When this is done, one gets the equilibrium blackbody temperature:

T_eq = 279 (1 - A)^1/4(r_p)^-1/2 K,  (r_p= distance from Sun to planet, in AU).

In most cases these match the appropriate temperature calculated above, but Venus and Jupiter disagree.  Venus has extra heating due to the greenhouse effect, while Jupiter has some internal heat source.  We will discuss both of these later.

So for Mercury, which is at r_p = 0.387 AU (semi-major axis), and has a very low Albedo of about 0.142, its sub-solar temperature is predicted to be about 605 K, while its equilibrium temperature would be about 431 K. These agree pretty well with accepted values of maximum temperature at the equator (about 700 K) and average temperature (340 K), keeping in mind that Mercury has a rather high eccentricity of 0.206, and it spends more than half of its time farther away that 0.387 AU. However, on the dark side of Mercury the equator temperature can be as low as 100 K (-173 C, or -279 F).

Dating Rocks

We can date the Earth by using radioactive decay of atoms.  Atoms come in many isotopes, all having the same number of protons, but different numbers of neutrons.  When an isotope has a lot of neutrons, it can be stable over a long period of time, billions of years, but still have some probability to decay to a more stable isotope.  An important example is ²³⁸U (a Uranium isotope with 238 nucleons--protons+neutrons), which decays to ²⁰⁶Pb with a half-life of 4.5 billion years.  This means that 1/2 of a sample of ²³⁸U will decay into ²⁰⁶Pb in 4.5 billion years.  Thus, one can take a sample of rock and compare the ratio of these two isotopes to get the age of the rock.  This works because ²⁰⁶Pb is a rare isotope in nature, so one can be quite sure that the rock had essentially none when it was first created.  Another pair of isotopes that is important for dating rocks is ⁴⁰K, which decays into the inert noble gas ⁴⁰Ar with a half-life of 1.3 billion years.  When a rock is remelted, the Ar escapes and the clock is reset, so the age one measures is the age since the last remelting of the rock.

When atoms decay, the change in the number is proportional to the number that exist (i.e., some fraction decay in a time dt).  The fraction is given by a constant of proportionality l.  The governing equation is

dn = -ln dt

which can be rewritten as:

dn/n = -l dt.

The integral of this equation is

ln n = -lt + constant

where the constant can be found by considering the initial conditions at time t = 0.  The solution is that the rock sample starts out a number n₀ at t = 0, so the solution is:

n = n₀e^-lt.

Now the half-life occurs when n = n₀/2 at time t = t, so

t = (ln 2)/l = 0.693/l.

Let's do an example.  A rock has a ratio ⁴⁰Ar to ⁴⁰K of 1 to 4.  How old is the rock, given that the half-life is 1.3 billion years?  This means that 1 out of 5 ⁴⁰K atoms have decayed to ⁴⁰Ar, so n = n₀ = 4/5.  Our equation then becomes:

4/5 = e^{-0.693 t / t}.

Solving for t, we get t = 0.322 t = 420 million years.

Mercury

Physical characteristics:  One solar day is 2 Mercury years long!  One sidereal day is 58.7 days, while one year is 88 days (2:3 ratio), so the synoptic rotation period is found by:

1/S = 1/P - 1/T = 1/58.7^d - 1/88.0^d = 0.00567 / day

so S = 176 days.  Mercury's bulk density is 5420 kg/m³, about the same as for Earth, but this turns out to be a puzzle.  Mercury is much less massive than Earth, so its gravity cannot squeeze rock to high density.  Thus, it must be made of naturally high density material--metals.  We infer a large metallic core (about 75% of the radius) covered with a rocky mantle. One possibility is that Mercury was once much larger, but suffered a massive collision that made it lose most of its outer mantel (Wikipedia article, Messenger link).

The albedo is quite low, at 0.142, giving a subsolar temperature of a whopping

T_ss = 394 (1-A)^1/4 (r_p)^-1/2 = 394 (0.96) (0.307)^-1/2 = 689 K (at perihelion).

Yet during the long solar night, the dark-side temperatures drop to 100 K.

Surface Features:
The Mercury Messenger spacecarft arrived at Mercury in March 2011, and is now busy making the most detailed maps and analysis of the planet ever. As you know, going to Mercury is energetically expensive!  The Messenger mission had to use several planetary encounters (with Earth, Venus, and Mercury) to reduce speed enough to get into Mercury orbit. The Messenger mission has 7 key questions it is trying to answer.

An earlier flyby mission, Mariner, 10 discovered a very weak, but present, magnetic field of 300 nT (nanotesla).  Earth's magnetic field is some 40000 nT, more than 100 times larger than Mercury. Still, this is large enough to deflect the solar magnetic field and solar wind, creating a small magnetosphere. First results just released from Messenger mapped the magnetic field and found the surprising result that its center is offset some 20% of Mercury's diameter toward the north. It was not clear until recently where such a magnetic field would come from, since Mercury rotates slowly, but recently it has been discovered that it has a liquid outer core, like Earth (although much thinner). 

Mercury's atmosphere, more properly called an exosphere, is very thin and consists of sodium atoms that are released from the surface by particle radiation and hang around for awhile but ultimately escape. It is of scientific interest to know the distribution of this exosphere, and in particular its dawn-dusk asymmetry, which can be observed from Earth during a transit of Mercury. A transit occurred earlier this year (2016 May 9), and was observed with NJIT's Big Bear Solar Observatory (see video). From these observations, the (preliminary) image in Figure 1a was obtained.

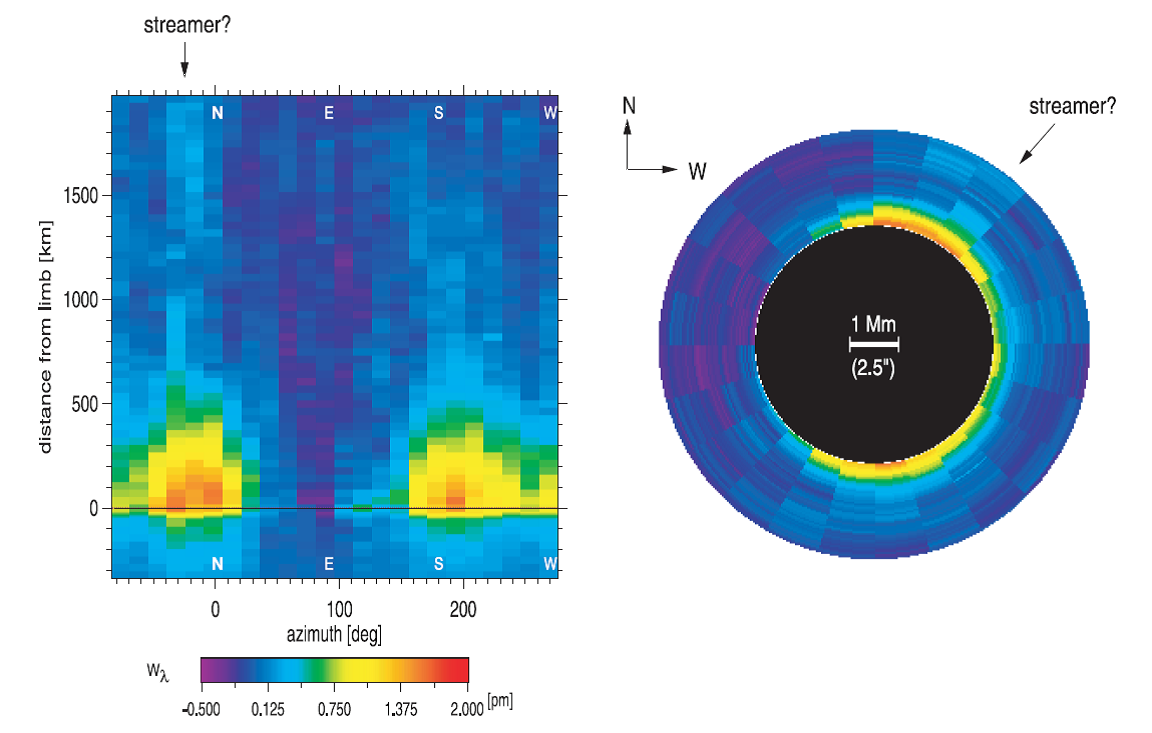Figure 1a: Preliminary data from the 2016 May 9 transit of Mercury across the Sun, taken with Big Bear Solar Observatory's FISS instrument, showing the distribution of sodium absorption in Mercury's atmosphere (dark feature extending above the planet). Carl Schmidt, private communication.	Figure 1b: A similar observation from the 2003 Mercury transit, with somewhat lower spatial resolution, but generally agreeing with the 2016 results shown in Fig. 1a. Schleicher et al. 2004, "Detection of neutral sodium above Mercury during the transit on 2003 May 7, A&A 425, 1119.

By taking images in many wavelengths, Messenger has made true-color and exaggerated color images. The images reveal something about the mineral makeup of the surface, as do true-color images like this one of the crater Degas.

BepiColombo mission (ESA)