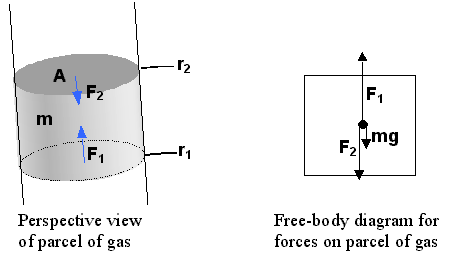
We now want to look at the internal pressure of Venus. It may seem that there is no way to know it, but if we think about the fact that the pressure on an element of mass is just due to the weight of all of the mass above it, we will see that it is not so hard to estimate. Pressure is force/unit area, F / A. Pressure in the interior of a planet arises from the inward force of gravity--balanced by the outward pressure due to the normal force of what is below it. Of course, Venus can be considered as static, meaning that it is not expanding or contracting. Such a state is called hydrostatic equilibrium, and like all equilibrium situations, it is characterized by force balance. Consider a column of cross-sectional area A. The forces on a section (parcel) of the column are shown in the figure on the left:
The mass of the parcel is related to the mass density by r = m/V = m/A(r2 - r1). From the free-body diagram it is clear that
F1 = F2 + mg = F2 + A(r2 - r1)rg
where g is the local acceleration of gravity (which obviously varies with depth in the planet). This force equation can be rearranged to
DF / A = DP = -Drrg
where DP is the pressure difference (P1 - P2) on the two ends of the column section, and Dr is the radius difference, or thickness of the parcel, (r1 - r2). Taking the limit as Dr approaches zero, we obtain the equation of hydrostatic equilibrium:
dP/dr = -rg = -r(r)GM(r)/r2 (1)
where M(r) is the mass interior to the radius r. This is the equation of hydrostatic equilibrium. Now, we cannot go further unless we know how the mass depends on radius, in other words, unless we know M(r). However, let's make an approximation that the interior of the Venus is of constant density, with r =<r> = 5200 kg/m3. Then the mass function will be:
M(r) = 4/3 pr3<r>,
and we can solve equation (1) by integrating:
dP = - <r>G (4/3) pr3<r>/r2 dr
from the center to the surface:
0 R dP = - <r>2 (4/3)pG r dr Pc 0
so
Pc = (2/3) pG <r>2 R2 = (1.4 x 10-10) <r>2 R2.
Using our bulk density of 5200 kg/m3, and the Venus radius of 6052 km, we find that the pressure at the center of the Venus is about 1.38 x 1011 Pa = 1.38 x 106 atm.
The SI unit for pressure is pascals, where 105 Pa = 1 atm = 1 atmosphere.
The actual pressure at the center of the Venus is about 3 x 106 atm, due to the fact that density is not actually constant with radius. By the same approach as above, we find that Earth's central pressure is about 23% higher (3.7 x 106 atm), due to its higher average density (5500 kg/m3) and slightly larger radius.
Venus appears completely cloud covered, with a high albedo (0.67). Swirling wind patterns can be seen in the clouds, as shown in the photos from Galileo, below:
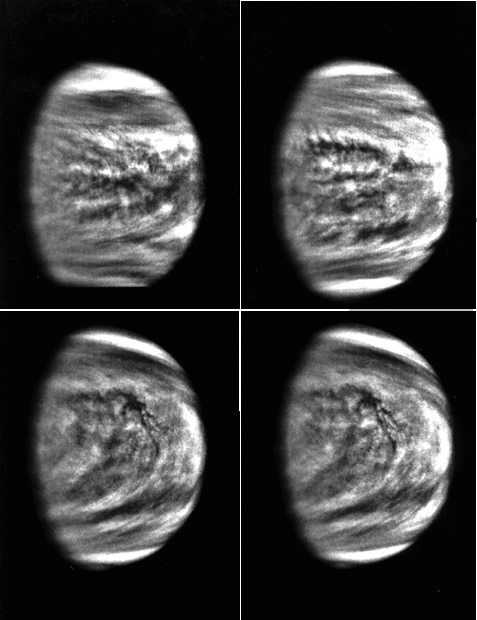
Images from Galileo 1 day apart, except the bottom two
images were taken 2 hours apart. Note that the clouds
are lagging behind at the equator, and the patterns move
right to left in the figure. The temperate zones have the
equivalent of Jet streams.
The clouds trap allow some visible light through, but trap infrared light due to the presences of greenhouse gases in the atmosphere.
 |
| Glass transmits visible light, but blocks infrared radiation. This is how greenhouses work. CO2 is an example of a greenhouse gas, which behaves in a similar way, letting solar radiation in but trapping heat. (from YouTube video https://www.youtube.com/watch?v=Fx49t4sv7f0 |
Venus' atmosphere is 96.5% carbon dioxide (CO2). Russia landed several landers on the surface, as shown in the accompanying images. The temperature and pressure conditions were so high that the landers survived only a few hours, despite their diving bell construction.

Venera 13 Lander images
Venera 14 Lander images

Because of the clouds, scientists in the 18th century used to speculate that Venus was a garden planet of lush tropical vegetation. We now know that it is more like biblical version of hell, with the clouds made of sulfuric acid, the atmospheric pressure at 95 atm and the temperature at about 740 K, hot enough to melt lead!
Surface Features:
You might think that we
could know very little about Venus' surface, since it is perpetually cloud-covered.
However, thanks to the Magellan Venus Orbiter, which was able to use radar
to map the entire surface, we now have extremely detailed images of the
surface, which includes the usual craters, but also volcanoes and many
features never seen on any other planet.
Let's look at some images of Venus (photo gallery)
- Why do you think the rays of ejecta from craters look so strange compared to the Moon or Mercury?
- Why are there few craters on Venus?
- Why is there so much apparent volcanism?