A: History of Solar System Models

1. The Ptolemaic System

The ancient model for the solar system is called the Ptolemaic system, because it was written down by Claudius Ptolemy (c. 100 AD) in his 13-book work, the Almagest, although it is an "obvious" model that originated in prehistory.  Also called the Earth-centered, or geocentric, system, it placed the immovable Earth at the center, with the Sun and planets going around it (attached to heavenly spheres).  Handed down from Aristotle (384-322 BC) was the notion that all motions having to do with the heavens had to be perfect, hence circular. Hipparchus (c. 150 BC) proposed a system of circles to explain the odd motions of the planets as seen from Earth.

Careful observations of the sky over many years show that planets obey certain rules.  They align with the Sun (conjunctions), where they often become faintest, and they appear opposite the Sun (opposition), where they become brightest.  Near opposition, planets sometimes stop, reverse direction (retrograde motion), then move forward again.  Two of the planets, Mercury and Venus, never wander very far from the Sun, and so reach a maximum angular distance, called greatest elongation.  These motions can be demonstrated in any planetarium program (e.g. stellarium).

The model of Aristotle, with planets moving in perfect circles around the Earth, could not account for these real planetary motions.  To explain such things as retrograde motion and the fact that planets vary in brightness,  Ptolemy introduced three "cheats:"

the eccentric

the epicycle

the equant.

Together, these adjustments, always involving perfect circles, could be adjusted to fit almost any situation within the accuracy of observations of his day (and for another 1500 years!).

Although suggested much earlier, the heliocentric model is attributed to Nicholas Copernicus who wrote the first "modern" description in his book, De Revolutionibus in 1543.  In this world-view, the Earth moves in a perfect circle about the Sun (the influence of Aristotle's perfect heavens idea), as do all of the other planets except the Moon (which was considered a planet), and the rotation of the stars and planets once every 24-hours was simply accounted for by the turning of the Earth on its axis.  Although this view is far simpler, and accounts more naturally for the motions of the heavens, it had three problems:

• A moving Earth did not agree with everyday experience.
• A moving Earth took it from its exalted place at the center of the universe.
• Although it could account for retrograde motion and the changing brightness of the planets, the planetary motions in perfect circles did not give better accuracy in planet positions than did the Ptolemaic system with epicycles.  [In De Revolutionibus, the Copernican model was justified as an alternative for calculation of planetary positions.]

We will see in a later lecture how the accuracy of the Copernican model could be improved, but first, let us examine the motions of the planets in the sky, and how they are accounted for by the geometry of the heliocentric model (Figures 1 and 2, below).
 

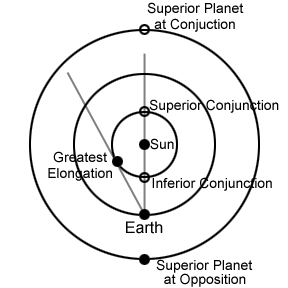
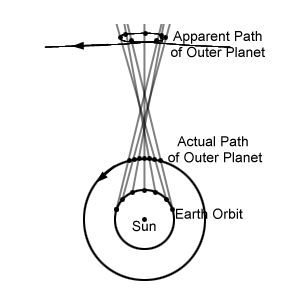
Figure 1: Geometry of planetary positions, showing greatest elongation, superior conjunction, and inferior conjunction, for inferior (inner) planets, and conjuction and opposition for superior (outer) planets.	Figure 2: Geometry of planetary motions, showing how retrograde motion arises from the orbital motions of Earth and a superior (outer) planet.

Figure 1 above shows why the inferior planets never wander too far from the Sun, but rather reach greatest elongation and then appear to move back toward the Sun.  They have both an inferior conjuction, when the planet lines up with the Sun on the near side, relative to Earth, and a superior conjuction, when the planet lines up on the opposite side of its orbit.  Figure 1 also shows how a superior planet reaches conjunction only once (this is a superior conjunction, actually), but when nearest the Earth is at opposition.  Figure 2 shows how retrograde motion for a superior planet occurs.

Copernicus derived a relationship  between the synodic period, S, of a planet, and its sidereal period, P, defined as follows:
 

Synodic Period:	Time for a planet to appear in the same place in the sky relative to the stars (in the same constellation).  This is as seen from Earth, and involves the motion of the Earth.
Sidereal Period:	Time for a planet to go once around the Sun (with respect to the stars).  This period is independent of where we are, and does not depend on the motion of the Earth.

Note that when we talk about orbital periods in this course, we will always mean sidereal period.  If you wish, you can keep these straight by the following mnemonic: as we pass by a planet, we "nod" at the synodic period.  The sidereal period, on the other hand, is the "real" period.

Consider one trip of a planet around the Sun as traversing 360^o.  Then the rate in degrees/year is just 360^o/P. where P is the sidereal period in Earth years.  Let's call the Earth's sidereal period P_Earth = E.  What is the value of E?  Since the Earth orbits in exactly 1 Earth year (by definition), E = 1.  The rate is then 360^o/E for Earth, and 360^o/P for another planet.  The synodic period, S, is the number of Earth years it takes for Earth to "lap" a planet (i.e., for an outer planet, it could be from opposition to opposition, while for an inner planet it could be from greatest elongation to greatest elongation).

Superior Planet: Let's derive an expression for the relationship between S and P for a superior (outer) planet.  The Earth has to go 360^o around, then go another n degrees to make up for the motion of the planet in one synodic period.  The rate for the Earth, though, is of course constant, so we have

 
 

360 + n		360		360		n		360
	=		==>		+		=		(1)
S		E		S		S		E

At the same time, the superior planet has only gone n degrees total distance around its orbit at its rate of 360/P, so

 

n		360
	=		(2)
S		P

Substitute this into equation (1), and we get:

 

360   360   360   1   1   1   + =  or  = -     (Superior Planet) S   P   E   S   E   P

 

By a similar argument, we arrive at a similar expression for an inferior planet:

 

360   360   360   1   1   1   + =  or  = -     (Inferior Planet) S   E   P   S   P   E

Example: Look up Venus' orbital (i.e. sidereal) period in Appendix C, table titled "Planetary Orbital and Satellite Data."  We find P = 0.6152 yr.  What is Venus' synodic period (with Earth)?  Use the expression for an Inferior planet

1 / S = 1 / 0.6152 - 1 / 1
        = 1.6255 - 1 = 0.6255
               (Note: keep 5 significant figures)

Therefore, the synodic period is

S = 1.599 yr (583.9 days)

Reasonable people, believing their own senses, would naturally accept the Ptolemaic (sun-centered) model of the universe.  But as more careful measurements were made, the Ptolemaic model had to be embellished in ways that became more and more artificial.

A simpler view, but one that seems to contradict common sense, is that the Earth is just one of the planets, and revolves around the Sun.  In this view the Earth, Sun, and another planet make alignments called opposition and conjunction.  For inferior (inner) planets we learned about other relationships: greatest elongation, inferior conjunction, and superior conjunction.  For superior (outer) planets we learned about retrograde motion.  We also learned about sidereal and synodic periods, and the relationship between them.