A. Meteor Showers

• Leonids (source Tempel-Tuttle)
• Orionids (source Halley)
• Perseids (source, Swift-Tuttle)
• Geminids (source Phaethon --asteroid?)

B. Asteroid Families

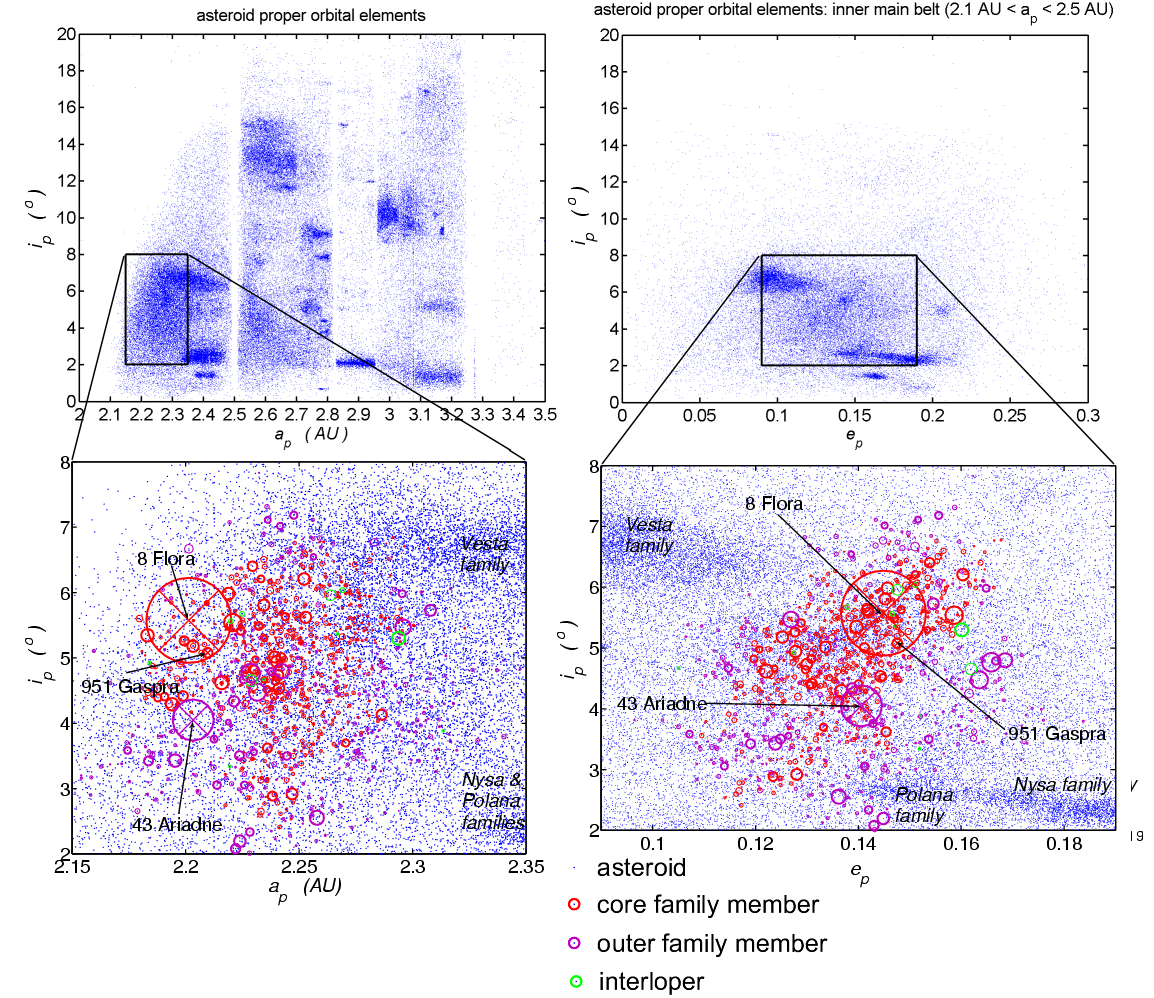
If one plots the number of main-belt asteroids vs. their semi-major axis, one finds some initially puzzling patterns--gaps in the distribution where there are missing asteroids. However, these gaps are exactly at resonances with Jupiter (3:1, 5:2, 7:3). Notice that there are very few asteroids with orbits closer to Jupiter than the 2:1 resonance at 3.27 AU, or farther away from Jupiter than the 4:1 resonance at 2.06 AU. Notice the dips at 2.71 AU and at 3.07 AU. These are the 8:3 and 11:5 resonances, respectively. These are called Kirkwood gaps, and show that Jupiter's gravitational influence is dominating these special zones of the asteroid belt, slowly perturbing them over millions of years and forcing them into different orbits. Note, there are no spatial gaps in the asteroid belt itself! These gaps are only in the semi-major axes.

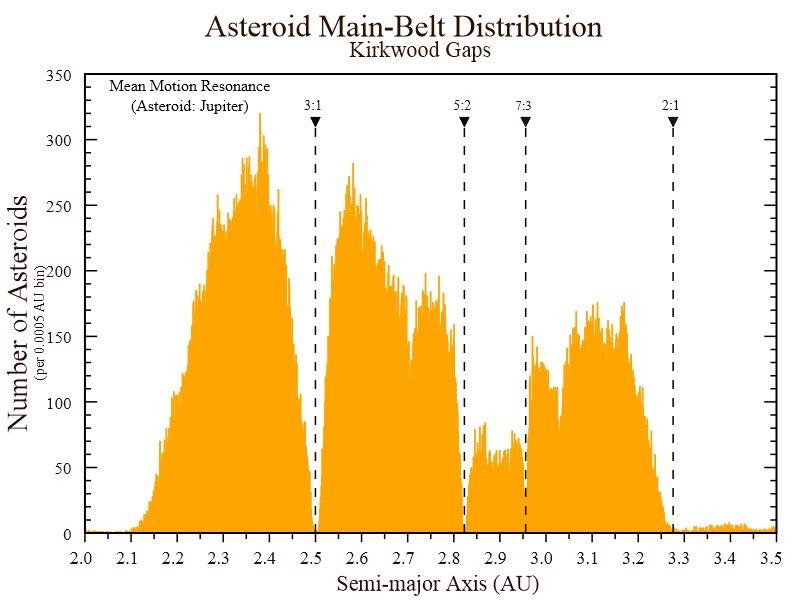
Other interesting patterns show up for plots of orbital parameters such as inclination vs. semi-major axis and inclination vs. eccentricity. Now several asteroid families begin to show up. Look carefully at the Koronis family, which is thought to be the result of a catastropic collision at least 2 billion years ago between two larger bodies. You can see evidence for perturbations having spread the semi-major axes between the 5:2 and 7:3 resonance gaps, but if they try to extend further they get wildly disrupted due to the resonance. This creates a sharp edge to the distribution. You can see similar edges in other families.

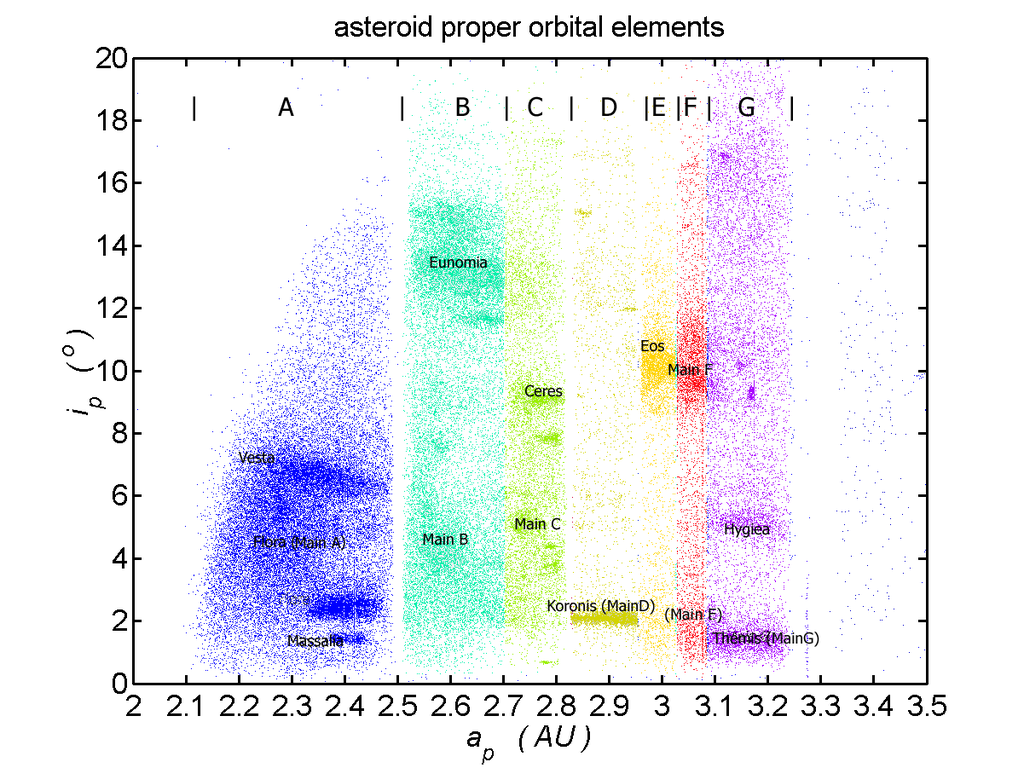
Let's take a closer look at the Flora family. This family of S-type asteroids lies close to the unstable zone of the asteroid belt due to a so-called secular resonance with Saturn. As a result, the Flora familiy is considered a good candidate for the L chondrite meteorites, which constitute 38% of all meteorites that are found on Earth. By studying these meteorites, radioisotope dating shows that the parent body was catastrophically disrupted around 470 million years ago.

C. Meteorites

Meteorites come in the same types as asteroids! We saw that L condrites may come from the Flora family of asteroids. What about the iron meteorites? Chemical and isotope analysis indicates that perhaps 50 different parent bodies were involved.

Sweeping out the solar system: Radiation Pressure and Poynting-Robertson effect.

The tail of a comet appears to be streaming behind the comet as it races across the sky.  In fact, their are two tails, and the reason for their streaming away from the comet are different.  In both cases, the tails point away from the Sun, even when the comet is itself moving away from the Sun--in that case the tails point ahead of the comet motion.  What is happening?

The two tails are:

• Ionized gas tail
• color is bluish
• main force is the solar wind
• solar wind speed is 400-800 km/s, comet's speed is about 30-50 km/s.
• tail is straight
• dust tail
• color is white (reflected sunlight)
• main force is photon (radiation) pressure
• particles are large and not much affected by the solar wind
• tail is curved

Photons have energy E = hn, where h = 6.62 x 10^-34 J s is Planck's constant.  They also have a corresponding momentum p = E/c.  Just like particles, they can "bounce off" an object and impart twice their momentum, or be absorbed by the object and impart their momentum to the object.  The energy flux from the Sun, as we have seen before, is F = L_sun/4pd², where L_sun is the solar luminosity (watts, or J/s) and d is the distance from the Sun.  Thus, there is also an associated momentum flux P = F/c = L_sun/4pcd², which has units of force/area, or pressure.  This is called radiation pressure.  Consider a dust particle of radius r, which intercepts this momentum flux over its cross-sectional area pr².  It will experience a force

F_R = pr²L_sun/4pcd² = (L_sun/4c)(r²/d²).

At the same time, the dust particle feels a gravitational force

F_G = GMm/d² = GM_sun(4pr³r/3)/d².

where r is the density of the dust grain.  It is interesting that these both depend in the same way on distance from the Sun, so that the ratio is independent of distance:

F_R / F_G = (pr²L_sun/4pcd²) / (GM_sun(4pr³r/3)/d²)

           = 3L_sun/(16pcGM_sunrr)
            = 5.8 x 10^-4 / rr.

where r must be expressed in kg/m³, and r must be expressed in m.  Note that for reasonable densities (r~ 1000 to 6000 kg/m³) the ratio is greater than one only for particles of size < r ~ 0.1 mm, so particles smaller than this size can be blown away from the Sun by radiation pressure.  This tells us that comet tails are made of very fine material.

For much larger particles, a new effect of the momentum of light becomes important.  As they orbit the Sun the photons come from slightly ahead of the object (they "run into" the photons), with the angle between the incoming photons and the radial direction being q = v/c.  This causes an ever-so-slight slowing down of the particles, so that they actually spiral into the Sun.  The component of the radiation force that opposes the orbital motion is qF_R = v/c F_R.  The time that it takes for a particle at size r, originally at a distance d (in AU), and density r (kg/m³) to spiral into the Sun is only

t = 7 x 10⁵rrd² years.

This is only about 3000 years for a 1 mm particle of density r = 4300 kg/m³.  Of course, particles of size 1 m take 1 million times longer, or 3 billion years.

There is another effect that has recently been considered, and that is the effect of differential emission of IR radiation from a body that is not at uniform temperature.  Recall that the sunlit and dark sides of a slowly rotating body can have considerably different temperatures, and will therefore emit different amounts of IR radiation.  If a body is rotating in the direct (CCW) sense, its "hot" side will be continually turning to face in the opposite direction to its motion, so the body will get a little boost and spiral away from the Sun.  If instead the body rotates in the retrograde (CW) sense, it will be slowed down and spiral toward the Sun.  This is a favored way for asteroids and smaller meteoroids to migrate into the Kirchwood gaps and get ejected from those orbits into the inner or outer solar system.