A. The Solar Interior

It may seem strange, but we know far more about the interior of the Sun than we do the interior of any planet, with the possible exception of the Earth. For many decades, this knowledge came from studies of stars, of which the Sun is but one example, and numerical (computer) models that incorporate our knowledge of physics. Each advance in our understanding of the Sun's interior could be checked by observations of thousands or millions of nearby stars (those within, say, 100s or 1000s of parsecs). Note that this is a major difference with respect to planets. We have only recently discovered the hundreds of extrasolar planets now known, with which to test our knowledge of planetary interiors. We will try to provide a flavor of how that process of investigation works. Starting in the mid-1970s, however, the discovery of solar oscillations revolutionized our study of the Sun's interior, and in the process also firmed up our knowledge of the interiors of other stars.

We will start with some simple scaling arguments like we did earlier for planets. First, the bulk density of the Sun is just <r> = M_sun/ 4/3pR_sun³ = 1410 kg m^-3. Its composition is given in terms of three ratios:

• X = m_Hn_H / <r> (ratio of density of hydrogen to bulk density)
• Y = m_Hen_He / <r> (ratio of density of helium to bulk density)
• Z = m_Zn_Z / <r> (ratio of density of everything else to bulk density)

At the surface of the Sun (and throughout most of its interior), we have the values X = 0.73, Y = 0.26, and Z = 0.01. This means that the Sun is mostly (>90% by number) hydrogen, the rest (~10%) is helium, with a tiny fraction being something else (e.g. carbon, oxygen, iron, etc.). These composition numbers come from spectral measurements of the light from the surface of the Sun, where we see many spectral lines from which the composition can be determined. However, the composition can change with depth in the Sun, mostly because the core of the Sun is a nuclear furnace that is converting hydrogen to helium through the process of nuclear fusion. To determine that, we have to rely on numerical models, and know the rate of this conversion, plus the overall age of the Sun. In example 10.1.1 of the text (which you have followed in homework problems to get planetary central pressure estimates) you can see that the equation

dP/dr = -G M(r) r(r)/r²

can be used to get a crude estimate (called a scaling law) for the central pressure by converting dP/dr to DP/Dr = (P_s - P_c)/ (R_s - 0) ~ -P_c / R_s, where the subscript c denotes central value and s denotes the surface value. The equation above can then be solved for the central pressure

P_c = -G M_sun<r>/R_s

where we are using the bulk values since the pressure at the center of the Sun is due to the overlying weight of the entire solar mass. This is equivalent to assuming that the density of the Sun does not change with depth (a poor assumption, but this is just an estimate). Plugging in the numbers, we obtain the central pressure estimate as 2.7 x 10¹⁴ N m^-2. Now what about the central temperature of the Sun?

The temperature, density, and pressure are not independent, but are joined by the equation of state, which describes the macroscopic manifestation of particle interactions.  One well-known example of an equation of state is the ideal gas law:

PV = NkT

where P = pressure, V = volume, N = number of particles, k = Boltzmann's constant, and T = temperature.  We can write this more simply in terms of the number density n = N / V as

P = nkT.

Note that the number density refers to individual particles, whether hydrogen atoms, helium atoms, or whatever. How do we count atoms? The way that composition plays a role in stellar structure is mainly through the mean molecular weight, defined in terms of its inverse as:

1/m = m_Hn / r                               (1)

where n is the number density (particles m^-3) of particles of all types, i.e. n = n_e + n_H + n_He + n_Z.  This is the number density of electrons plus all of the kinds of atoms.  A good approximation for most star interiors is that the gas is fully ionized.  For a fully ionized gas, how many electrons will there be?  Each hydrogen atom will contribute 1 electron.  Each helium atom will contribute 2, and each higher element will contribute Z (that is, a number equal to the atomic number of the element).  In this case, we have the mean molecular weight given by:

1/m = 2 X + 3/4 Y + 1/2 Z

where the X, Y and Z are as given above. Again, for the Sun (at the surface and throughout much of the interior), X = 0.73, Y = 0.26, and Z = 0.01, so m ~ 0.6.

Solving for n in equation (1), we see that the number density is related to the mass density by

n = r /mm_H

so the equation of state becomes

P = rkT / mm_H .                       (2)

Finally, solving for T and using our estimate of central pressure above, we get for the central temperature

T_c = P_cmm_H / <r>k = 1.44 x 10⁷ K.

This gives for the central temperature more than 14 million K, which is enough to permit nuclear fusion. Note that this high temperature is a consequence of the huge mass of the Sun pressing down on the center, and the behavior of gas particles under such huge pressure through the ideal gas law. There are many important physical effects we have ignored, such as the increasing density with depth, and the changing composition, but our estimates for Pc and Tc are actually pretty good. The actual values are obtained from the "standard model," which properly accounts for all that is known about the interior, about other stars, and properly accounts for the full physics.

Using scaling arguments, we have seen that the average density, core pressure and core temperature are as given in the table below.  These are contrasted with the more exact values determined from computer models of the Sun's interior (the so-called standard model).  We also show the mass fraction of hydrogen (X) and of helium (Y) at the surface and at the core.
 

From Scaling Arguments		From Standard Model
Core Temperature	1.4 x 107 K	Central Temperature	1.58 x 107 K
Core Pressure	2.7 x 1014 N m-2	Central Pressure	2.50 x 1016 N m-2
Average Density	1410 kg m-3	Central Density	1.62 x 105 kg m-3
X at surface	0.73	X at core	0.336
Y at surface	0.26	Y at core	0.643

The Sun is about 4.52 billion years old, and has been converting hydrogen to helium in its core all that time.  More than half of the hydrogen has been used up already, in the core, so the Sun is about middle-aged.  The solar model can be traced in time from an initial composition through to its present age.  As the composition changes due to using up the hydrogen, the other parameters of the Sun such as its radius, temperature, and luminosity must change as well.  According to the figure below, the solar radius has increased by about 12% over its lifetime, the surface temperature has increased by about 20%, and the luminosity (4pR²sT⁴) has increased by 30%.  However, this implies about a 5% increase in the last 500 million years, and it is not clear that such an increase is compatible with known Earth climate history.

Theoretical understanding of how the radius, temperature, and luminosity of the Sun has
changed over the lifetime of the Sun.  The changes may be more extreme than actually
occurred, given what we know of Earth's climate history.  Figure from Carroll and Ostlie,
Introduction to Modern Astrophysics, 2nd Edition, Addison-Wesley, New York, 2007.

Computer models such as the standard model must fit the observable constraints that we have, e.g. the mass, radius, surface temperature, luminosity, and composition.  We have some other constraints such as the age of the solar system (4.5 billion years), but we would like to have other information to be sure that the model is correct.  Currently, we have two additional methods, both pioneered in the 1970's, that actually let us "see" inside the Sun.  These are

• solar neutrino detections
• helioseismology

One of these, helioseismology, agrees spectacularly with the standard model and can give us information about the interior rotation of the Sun.  For a time in the late 1990s, the other, solar neutrino measurements, disagreed rather spectacularly!  The nuclear reactions that occur in the solar interior (the proton-proton chain) are:

 

PP I Chain (69%)
	11H +		11H =>		21H + e+		+ ne
	21H +		11H =>		32He + g
	32He +		32He =>		42He +	2	11H

 

PP II Chain (31%)
	32He +		42He =>		74Be + g
	74Be +		e- =>		73Li	+ ne
	73Li +		11H =>		2 42He

 

PP III Chain (0.3%)
	74Be +		11H =>		85B + g		+ ne
			85B =>		84Be + e+		+ ne
			84Be =>		2 42He

The electron neutrinos in each reaction are highlighted.  Neutrinos are rather mysterious particles, nearly or completely massless and very unreactive.  They pass through the Sun as if it were not there, so while photons reach us from the core only after 1 million years of torturous meandering, neutrinos come directly to us.  However, if traveling 700,000 km through a star cannot stop them, how can we detect them?  The neutrino in the yellow cell, above, can be captured by a Chlorine-37 nucleus in the following reaction:
 

Neutrino Capture (Homestake)
3717Cl		+ ne	=>		3718Ar + e-

In the Homestake Gold Mine in South Dakota, a tank of 100,000 gallons of cleaning fluid (C₂Cl₄) acts as a neutrino detector, in a pioneering experiment by Raymond Davis.  Every several months the tank was purged to detect the Ar atoms produced in the reaction.  From the standard solar model, it is expected that only slightly more than 1 atom per day will be produced among the 10³⁰ Chlorine atoms in the tank!  In fact, Davis only found less than 1 every two or three days.  Other experiments have been set up to detect neutrinos, including the far more numerous neutrinos produced in the PP-I chain (purple cell, above).  Results of all of the experiments indicate that the number of neutrinos detected is not consistent with the standard model.

Helioseismology is the study of "seismic" pressure and gravity waves inside the Sun.  Just as we can study earthquakes to learn about the Earth's interior, we can also study "sunquakes" to learn about the Sun's interior.  Sound waves are generated randomly, probably mostly from small-scale convective turbulence near the surface of the Sun.  They rattle around inside the Sun, but those modes that are at special wavelengths to match spherical harmonics of the Sun can live a long time and resonate inside the Sun. 

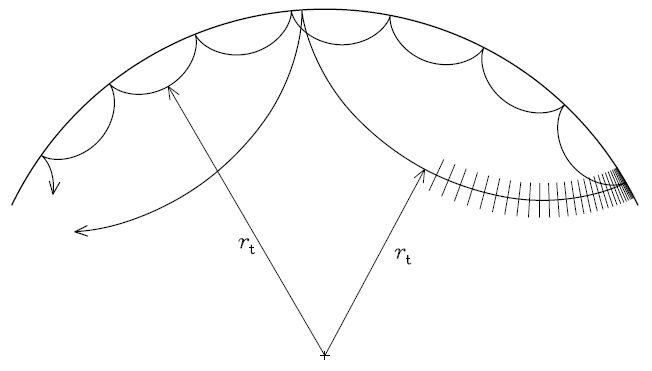
Diagram of two waves of different wavelengths being "launched" from the same point near the surface of the Sun at the right.
The longer wavelength wave propagates to a greater depth before refraction causes it to turn upward, so this mode samples
deeper into the interior. Each wave also reflects from the surface. Waves that bounce exactly an integral number of times and
come back to the same point form the "normal modes" and have long lifetimes, causing the Sun to reverberate like a bell.
From "Lecture Notes on Stellar Oscillations" by Joergen Christensen-Dalsgaard (http://users-phys.au.dk/jcd/oscilnotes/)

The wavelength-frequency (k-w) relationship of these resonances tell us the structure of the inside of the Sun.  The results of helioseismology agree very well with the standard model.

Neutrino Problem is Solved:
In 2001, some measurements with a new neutrino detector appear to have finally solved the mystery.  Here are the key ingredients:

• neutrinos come in three flavors, electron, muon, and tau.
• The Sun produces only electron neutrinos
• Before now, only electron neutrinos could be counted, and they indicated too few neutrinos--something is wrong.
• The neutrinos have mass, and because of that they may "oscillate" among the three forms.
• A new detector at the Sudbury Mine in Canada can detect both "neutral current" and "charged current" reactions
  • neutral current is when the reaction with deuterium produces a proton and a neutron (a simple split of the deuterium atom).  All three flavors of neutrino cause this kind of reaction.
  • charged current is when the reaction with deuterium produces two protons and an electron.  Only electron neutrinos cause this kind of reaction.
• The neutral current reactions allow all neutrinos to be counted, while the charged current reactions allow the proportion of electron neutrinos to be counted.
• The new results show that the total number of non-electron neutrinos (actually determined from Super Kamiokande in Japan) is increased in the same proportion that the electron neutrinos are decreased, indicating that the electron neutrinos are indeed changed to one of the other flavors.
• The measurement allows the electron neutrino mass to be estimated to be between 0.05 to 0.18 eV

C. Solar Atmosphere

The Sun does not end at its surface (the photosphere).  The matter of the Sun extends far out into interplanetary space, and these regions are referred to as the Sun's atmosphere.  Different regions of the atmosphere have different characteristics:
 

Solar Atmosphere	Characteristic
Photosphere	Where the coninuum is formed (H-)
Chromosphere	Where spectral lines are formed
Transition Region	Region of rapid drop in density,  rapid rise in temperature
Corona	Extended, thin, million degree gas,  seen during solar eclipse
Solar Wind	400-800 km/s flow of gas  into IP space