 |
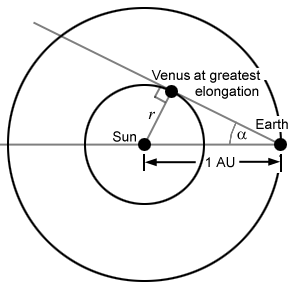
Greatest Elongation is a, and we want to determine the distance, r, of Venus from the Sun, in AU (Astronomical Units). The relationship is just r = sin a. |
| Physics 320 |
|
Prof. Dale E. Gary
NJIT |
Kepler's Laws
Support for the Heliocentric Model
Although Copernicus set down the basic principles of the heliocentric model, it was regarded as simply an alternative way of thinking about the universe, without any certainty that the Earth really moved. Two later scientists, Galileo and Kepler, gave several strong arguments in favor of the heliocentric model.
Galileo gave observational evidence:
Kepler gave direct, mathematically rigorous evidence:
Moons of Jupiter: gave clear evidence of smaller objects circling larger objects (although no one knew why--see also) Phases of Venus: gave clear evidence that Venus circles the Sun Sunspots on the Sun: gave clear evidence that heaven is not "perfect" Craters and Mountains
on the Moon:gave clear evidence that the Moon is another "world"
Let's look at how Kepler determined his first Law. First, he showed how to measure the relative distance to the inner planets (Mercury and Venus) by measuring their angle of greatest elongation, a:
Kepler's Three Laws (qualitative version) First Law: Planets travel in elliptical orbits with the Sun at one focus Second Law: Planets move more slowly in their orbits when far from the Sun than when close to the Sun Third Law: Planets with larger orbits move more slowly than planets with smaller orbits.
 |
Greatest Elongation is a, and we want to determine the distance, r, of Venus from the Sun, in AU (Astronomical Units). The relationship is just r = sin a. |
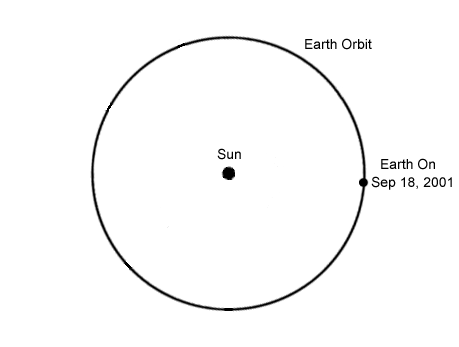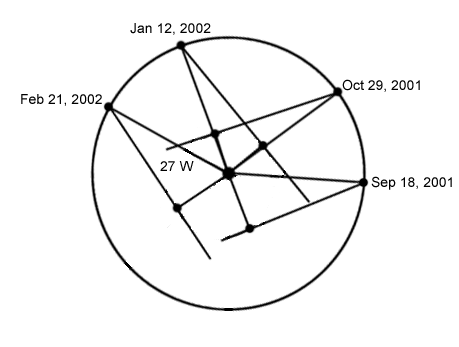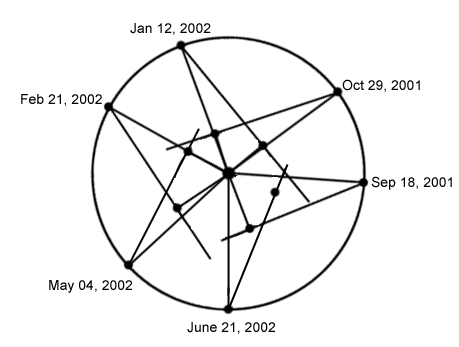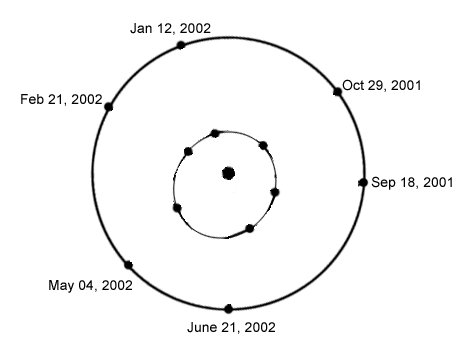 |
Animation showing the six consecutive greatest elongations of Mercury listed above. The position of Earth is advanced the appropriate number of degrees around its orbit for each date, then the line to Mercury is drawn East or West of the Sun as needed. Mercury is on this ray, at the point that the ray passes closest to the Sun. |
By measuring Mercury's greatest elongation from many places along Earth's orbit, any variation in distance of Mercury from the Sun can be determined.
The situation for the outer planets is harder, but can be done. Kepler did it by observing the outer planet at pairs of times separated by one sidereal rotation of the planet. Here is an outline of how this is done, for one pair of observations of Mars:
Kepler repeated this procedure for many pairs of measurements of the planet Mars, taken by the excellent observer, Tycho Brahe, and was able to show that the distance r varies with time in the way expected if the path were an ellipse! You can see that this is not easy, and requires extremely good observations of elongation angles.
Determining distance of outer planet from Sun: Take two measurements of the elongation (angle from the Sun) of Mars, one sidereal period (687 days) apart. Earth is at location E' at the time of the first observation, goes once around its orbit and arrives back at location E (almost completing two orbits) after Mars has gone around once.
The figure below shows the situation at a larger scale, with the angles labeled. The two elongation angles are e and e', and we also know the angle n, which is just the number of degrees less than two full orbits that the Earth makes in 687 days. You should be able to show that n = 42.89 degrees.
Since triangle DSEE' is isoceles, we can determine a, (you should be able to show that it is 68.56 degrees) and hence the length EE' (use the Law of Sines to show that it is 0.73 AU). Subtract a from e and e', which allows us to solve for triangle DEPE'. Finally, using the Law of Cosines for triangle DSPE', we can determine the distance r. 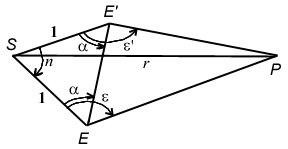
C. Kepler's Laws
1. Ellipses
In order to talk quantitatively about what Kepler discovered, we first need to remind ourselves of the properties of an ellipse.2. Orbits as Ellipses
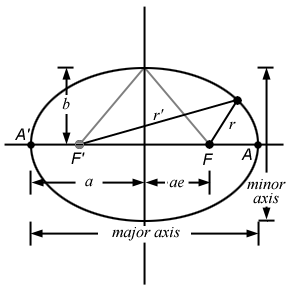
Properties of the Ellipse:
- Semi-major axis a = half of the long axis of ellipse
- Semi-minor axis b = half of the short axis of ellipse
- Eccentricity e = distance of focus F from center, in units of a. The eccentricity ranges from 0 (a circle) to 1 (a parabola).
- Sum of distances of a point on the ellipse from the two foci (r and r') is a constant: r + r' = 2a.
The triangle at right is 1/2 of the triangle formed by the light gray lines in the figure above. Convince yourself that the lengths of the sides are as shown. By the Pythagorean Theorem, show that the following relation holds: b2 = a2(1 -e2). 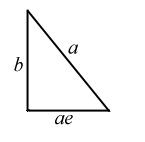
We would like to have an equation for the ellipse, and it is most convenient to express it in polar coordinates, relative to an origin at the focus F. A point on the ellipse P(r, q) will then have polar coordinates r and q, as shown in the diagram below. In the case of planetary orbits q is called the true-anomaly.
Equation for an Ellipse, in Polar Coordinates: The coordinates of a point on the ellipse are (r,q). The triangle DFPF' has sides of length r, r', and 2ae. Thus, by the Law of Cosines:
r' 2= r2+ (2ae)2 - 2r(2ae) cos(p - q) but remember r + r' = 2a, or r' 2 = (2a - r)2., so combining these and solving for r, we have the polar equation for an ellipse:r = a(1 -e2) / (1 + e cos q)
The above properties belong to all ellipses, but when the ellipse represents a planetary orbit, some of these variables have special significance. Here are some of them:
The equation for an ellipse is again:4. Kepler's Lawsr = a(1 -e2) / (1 + e cos q) (equation for an ellipse)and if we set the eccentricity, e, to zero, the equation reduces tor = a = constant (equation for a circle -- e = 0)while if we set e to 1, the equation reduces tor = a(1 -e)(1 + e) / (1 + e cos q)Thus, the eccentricity parameter determines how "stretched-out" the ellipse is. Note that the eccentricity can even be greater than one, in which case we have the equation
= 2p/ (1 + cos q) (equation for a parabola -- e = 1)r = a(e2- 1) / (1 + e cos q) (equation for a hyperbola -- e > 1)Note that the above equation cannot be derived from the equation of the ellipse, as we could the limiting cases for e = 0 and e = 1, but rather must be derived from the cartesian equation for a hyperbola (see Wikipedia, for example). The circle, ellipse, parabola, and hyperbola are all conic sections, and they all represent possible orbit shapes. We will see later how the total energy of the orbiting object will determine which of these shapes it follows.
We repeat once more Kepler's Laws, but being a bit more quantitative:D. What we have Learned
Kepler's Three Laws (quantitative version) First Law: Planets travel in elliptical orbits with the Sun at one focus, and obey the equation r = c / (1 + e cos q), where c = a(1 -e2) for 0 < e < 1. (Comets and other bodies can have hyperbolic orbits, where c = a(e2 - 1), for e > 1.) Second Law: The radius vector of a planet sweeps out equal areas in equal times (planet travels fastest when near perihelion). Third Law: The square of the orbital period of a planet is proportional to the cube of its semi-major axis: P2 = ka3, where k is a constantNote: Kepler showed that this relationship also held for the newly discovered moons of Jupiter by Galileo, but with a different value for the constant k! One consequence of this law is that inner planets travel faster than outer planets, also.
Careful measurements (by Tycho Brahe) were used by Kepler to measure the orbits of the planets and show that The Earth Moves! Kepler's Laws prove quantitatively that the true situation is given by a heliocentric model in which the planets revolve around the Sun. Kepler showed that the planets move in ellipses. We learned the important terms for ellipse characteristics: focus, semi-major axis, semi-minor axis, eccentricity, and for elliptical orbits, the terms perihelion and aphelion. We examined the characteristics and mathematical formulas for conic sections (ellipse, parabola, and hyperbola).
Kepler thought that there was a clockwork universe of crystal spheres, arranged harmonically (in certain ratios, related to regular geometric solids), but we will see next time that Newton was able to put it all on a firm physical foundation with his Law of Universal Gravitation.