| Physics 320 |
Astrophysics I: Lecture #5
|
Prof. Dale E. Gary
NJIT
|
Newtonian Mechanics
A: Dynamics
We are now going to study
orbits in some detail, but first we need to review some basic mechanics
such as you learned in your Freshman Physics class. In particular,
we need to review:
-
motion (coordinates, vectors,
velocity, acceleration)
-
linear momentum
-
forces
We will especially be working
in polar coordinates, which are the natural coordinate system for orbital
motion. In the next lecture we will review additional topics in basic
mechanics--angular momentum and energy.
1. Coordinates and Vectors
Recall that in three
dimensions, a vector equation really represents three equations, one for
each spatial dimension. A vector equation like
r = ro
+ vot
really represents the three
equations
x = xo
+ vox t
y = yo
+ voy t
z = zo
+ voz t
where the coordinates of the
vectors are
r = (x, y, z)
ro
= (xo, yo,
zo)
vo
= (vox, voy,
voz).
Legal vector operations are
addition and subtraction, e.g.,
v + u = u
+ v
(v - u)
+ w = v - (u-w)
of multiplication by a scalar,
e.g.,
av = va
a(v + u) = av
+ au , etc.
Ordinary multiplication of two
vectors generally has no meaning, but there are two special ways to "multiply"
vectors that are defined: the dot product
and the cross product.
a. Dot Product (or scalar
product)
v . u = vxux
+ vyuy
+ vzuz
= |v||u| cos q
(a scalar)
The meaning is " the component
of v in the direction
of u times the magnitude
of u," or equivalently,
" the component of u
in the direction of v
times the magnitude of v."
Example:
A box sliding down an incline
b. Cross Product (or vector
product)
|
| |
x y
z |
| |
|
| v x u
= |
| |
vx vy
vz |
| |
= (vyuz-uyvz)
x-
(vxuz-uxvz)
y
+ (vxuy-uxvy)
z
(a vector) |
|
| |
ux uy
uz |
| |
|
where x, y, and z are
unit vectors.
The magnitude is
| | v x u
| = vu sin q
(area of parallelogram) |
|
and the direction is perpendicular
to both v and
u.
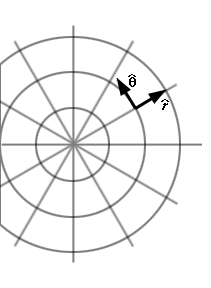
c. Unit Vectors
Note that polar coordinates,
(r, q),
are related to rectangular (2-D) coordinates (x, y)
by
r = ( x2
+ y2 ) 1/2
; q = tan-1
( y / x )
or conversely
x = r cos q
;
y
= r sin q.
Unit vectors are vectors of
length 1, e.g. the x, y, and z
above. Unit vectors in polar coordinates are:
r = cos q
x
+ sin q y ;
q = -sin
q
x
+ cos q y
and have directions in the r
and q directions,
respectively. Graphically:
 |
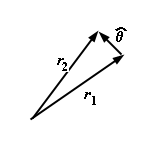
Note that
dr /dq
= q
|
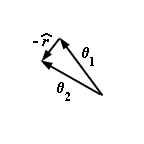
 |
and
dq/dq
= -r
|
 |
d. Time Derivatives, Velocity
and Acceleration
In rectangular coordinates,
the 2-dimensional position, velocity, and acceleration are as follows:
r = xx + yy
(position)
|
|
| v = dr / dt = |
r' (prime notation) |
|
=
|
dx/dt x + dy/dt y
= vx x+
vy
y
(velocity) |
| a = dv / dt = d2r
/ dt2 = |
r" (prime notation) |
|
=
|
d2x/dt2x
+ d2y/dt2y
= ax
x+
ay
y
(acceleration) |
In terms of polar coordinates,
things are a little more complicated:
r = rr
|
|
| v = (d/dt) rr
= |
r'r + r dr/dt = rr
+ r dr/dq
dq/dt = r'r + rq'q |
| |
|
|
==>
|
vr
= r' ; vq
= rq' |
| a = dv / dt = |
(d/dt)(r'r + rq'q)
= r"r + r' dr/dq
dq/dt + r'q'q+
rq"q+
rq'dq/dq
dq/dt |
| |
|
|
=
|
r"r + r'q'q+
r'q'q+
rq"q
- rq'2r
= (r" - rq'2)r
+ (rq" + 2r'q')q |
|
|
|
==>
|
ar
= r" - rq'2
; aq
= rq" + 2r'q' |
B. Newton's Laws
I. Law of Inertia
Newton's first law
is basically a statement of conservation of linear momentum, p
= mv. The law states:
| "The velocity of a body
remains constant unless the body is acted on by an outside force."
or
"A body at rest tends to
remain at rest, a body in motion tends to remain in motion, unless acted
on by an outside force.."
or
dp/dt = 0 ==> m dv/dt = 0
==> ma = 0 |
II. Force Law
Newton's second
law defines the force on a body in terms of its effect in accelerating
the body. The law states:
| "The acceleration imparted
to a body is proportional to and in the direction of the force applied,
and inversely proportional to the mass of the body."
or
F = ma |
Note that if m = constant,
this can be written
F = m dv/dt = d/dt mv
= dp/dt
This can be thought of as the
definition of force. If you pull or push a 1 kg body, and it is observed
to accelerate by 1 m/s, you have applied a force of 1 N (newton).
III. Action and Reaction
Newton's third law
is basically a statement of conservation of total linear momentum for a
system of particles. The law states:
| "For every force acting
on a body, there is an equal and opposite force exerted by the body."
or
F1
= - F2
or
P = S pi
=
constant |
C. Law of Universal Gravitation
Newton was interested in
explaining the motion of the Moon. He knew its distance fairly accurately,
and that it orbited the Earth with a nearly uniform circular motion.
In uniform circular motion,
the magnitude of v is
constant, but the direction changes. This turning of the velocity
is due to a central force, called the centripetal force, which gives the
body a centripetal acceleration (towards the center of its circular path).
The centripetal acceleration can be found by considering the velocity at
two points on the circle, and taking the limit,
| |
Dv |
|
dv |
|
|
lim
|
|
= |
|
= a |
| Dt=>0 |
Dt |
|
dt |
|
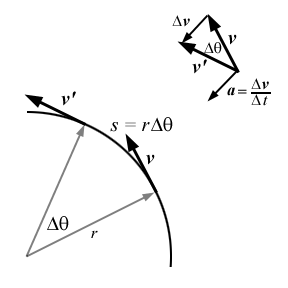
Diagram showing centripetal
acceleration for an object in uniform circular motion. The centri-
petal acceleration needed to "turn" the velocity from v to v'
is Dv/Dt,
where the relationships between s, Dv
and Dq are
as shown. |
From the drawings above,
we have
s = r Dq
= v Dt and Dv
= v Dq ==> Dv/Dt
= v2/r
so
a = v2/r
(centripetal acceleration)
Note that the velocity here
is only in the theta direction, vq
= r dq/dt,
so we can recognize the second term in our earlier, general expression
for radial acceleration as the centripetal acceleration, complete with
minus sign to indicate that it points inward toward the center:
| ar
= r" - rq'2
= r" - vq2/r |
The force is F
= ma, so the Moon must experience
a force F = mv2/r,
where m = MMoon
= mass of the Moon, v =
orbital velocity of the Moon, and r = DMoon
= distance to the Moon from the center of
the Earth (actually from the center of the Earth-Moon system, as we will
see later).
It may seem hard to measure
the velocity of the Moon--how would you do it?
Just use its period and the
length of its orbit (2pDMoon)
to get v = 2pDMoon/P,
which gives
|
mv2 |
|
MMoon(2pDMoon/P)2 |
|
MMoon4p2DMoon |
| F = |
|
= |
|
= |
|
|
r
|
|
DMoon
|
|
P2
|
But recall that Kepler gave
the relationship between the period and radius (semi-major axis) of an
orbit, which in this case is: P2
= kDMoon3,
which gives
|
|
MMoon4p2 |
|
| F |
= |
|
==> inverse square law Fa
1/r2. |
|
|
kDMoon2
|
|
From Newton's third law, he
knew that the force of the Earth on the Moon must be balanced by an equal
and opposite force of the Moon on the Earth, so the force had to
be proportional to both masses:
|
|
MMoonMEarth |
|
GMm |
| F |
a |
|
= |
|
|
|
r2
|
|
r2
|
Of course, the force is attractive,
directed along the radius vector, so the vector force is
Newton now took at leap of insight,
and considered this law to be valid everywhere, i.e. it is a Universal
Law. In particular, he could measure the force on an object at the
surface of the Earth:
|
|
GMEarthm |
|
|
| F |
= - |
|
r = |
-mgr |
|
|
REarth2
|
|
|
which allowed him to relate
his constant, G, to the acceleration of gravity at Earth's surface:
If his law was Universal, then
the magnitude of the force on the Moon would be
|
|
GMEarthMMoon |
|
REarth2 |
|
| F |
= |
|
= gMMoon |
|
= g' MMoon |
|
|
DMoon2
|
|
DMoon2 |
|
Could it be so simple?
Is the Moon merely "falling" with this value of acceleration? To
find out, Newton needed to show that the acceleration needed to keep the
Moon in its orbit was related to the acceleration of a stone falling at
the Earth's surface, according to this relationship (working with accelerations
rather than forces avoids the need to know the Moon's mass). To show
this, Newton considered the distance the Moon must "fall" towards Earth
in one second.
The value of g'
,
above, is
g' = 9.8 m/s2
(REarth/DMoon)2
= 2.71 x 10-3
m/s2.
Thus, in 1 s, the Moon will
fall a distance
d = 1/2 g't2
= g'/2 = 1.36 x 10-3
m (1.36 mm).
Let's see if this matches the
orbit of the Moon. The sidereal period of the Moon is P =
27.32 days = 2.36 x 106
s, so the angular velocity is 2p/P
= 2.66 x 10-6
s-1.
Thus, in 1 s, the Moon moves through an angle of 2.66 x 10-6
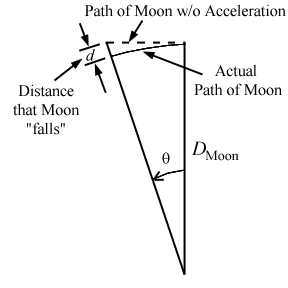
radians. The distance that the Moon falls is shown in the figure
below, and is related to the distance to the Moon by
d = DMoon/cos
q
- DMoon
= -DMoon
(1 - 1/cos q) .
We cannot use most calculators
with such a small angle (most will just give cos 2.66 x 10-6=
1), but we can expand as a power series, which
for such a small angle will allow us to keep only the leading terms.
We will need two expansions:
cos q = 1 -q2/2
+ q4/24
-
...
(1 - x)n
= 1 + nx + 1/2n(n-1)x2
+ ...
where the second expansion is
used to expand the result of the first expansion, in the form (1
-q2/2)-1.
Performing these expansions and keeping only the leading term, we find
that
d = DMoonq2/2
= (384,000 km) (2.66 x 10-6)2
/
2 = 1.36 x 10-3
m.
The same answer! So Newton
finally understood the truth! The Moon is falling towards Earth just
like any stone or apple would do. The Law of Gravitation truly is Universal!