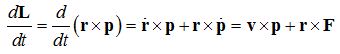| Physics 320 |
Astrophysics I: Lecture #6
|
Prof. Dale E. Gary
NJIT
|
Orbital Mechanics I
A: Physical Interpretation
of Kepler's Laws
Kepler's first law states
that the planets move in elliptical orbits around the Sun, with the Sun
at one focus. Elliptical orbits are indeed a property of inverse
square law central forces, as we will show shortly.
Let us examine Kepler's second
and third laws in view of Newton's Law of Universal Gravitation.
1. Law of Areas and Angular
Momentum
Kepler's second
law states that the radius vector between the Sun and an orbiting planet
sweeps out equal areas in equal times. Consider a planet moving along
its elliptical orbit at a distance r,
with velocity v, as in the figure
below.
 After a time Dt,
it moves an angular distance from point P to point Q of
After a time Dt,
it moves an angular distance from point P to point Q of
Dq
= vq Dt
/ r .
During this time, the radius
vector sweeps out the triangle FPQ, whose area is DA = 1/2 rvq Dt, so
| |
DA |
|
dA |
|
r vq |
|
|
|
lim
|
|
= |
|
= |
|
= |
1/2 r2q' |
| t --> 0 |
Dt
|
|
dt
|
|
2
|
|
|
According to Kepler's law, dA/dt
= constant, and in particular after one complete period
P,
the area swept out is the total area of the ellipse,
dA/dt = A/P = pab/P
= constant = rvq/2.
There are two places in its
orbit where the radial velocity, vr,
of a planet goes to zero, and it has only v = vq
--these
are at aphelion and perihelion. At these locations, the speeds obey
the relation
v = 2A/Pr = 2pab/Pr
but at perihelion, r
= a(1 - e)
and at aphelion r = a(1 + e),
so
vperi
= 2pab/Pa(1
-
e)
vap
= 2pab/Pa(1 +e)
but remember our relation b
= a (1 - e2)1/2,
so these become
vperi
= (2pa/P)[(1 +e)/(1 -
e)]1/2
vap
= (2pa/P)[(1
-
e)/(1
+ e)]1/2
Example:
What are vperiand
vap
for Earth orbit?
P = 365.26 days = 3.156 x 107
s
e = 0.0167, a = 1 AU = 1.496 x 108
km
vperi =
(2pa/P)[(1
+e)/(1 - e)]1/2=
30.28 km/s
vap =
(2pa/P)[(1
-
e)/(1
+ e)]1/2=
29.28 km/s
Again, this result shows that
planets move faster near the Sun, but the Earth's orbit is so nearly circular
that the speed does not change much. App for planetary orbits.
Angular Momentum:
What does all of this have
to do with angular momentum? Recall that angular momentum is a measure
of rotational motion about a center of rotation--usually the center of
mass (but if an object is "pinned," the center of rotation is about that
pinning point).
This system has zero angular
momentum This system has non-zero angular
momentum
The angular momentum is given
by
L = r
x p
where p = mv
is the linear momentum. In magnitude, this is |L| =
L
= rp sin q = rpperp.
But
in polar coordinates, pperp=
mvq,
so
so this is the appropriate expression
for the angular momentum of a planet about the Sun. The key is to
examine how the angular momentum changes around the orbit, i.e.,
but v x p
= mv x v = 0
dL/dt = r x F
(this is the torque on the planet)
For any central force, in particular
for Newton's Law of Universal Gravitation, where F = -
(GMm/r2) r,
we are going to have r x F = 0
also! Thus,
dL/dt = 0; so
L = constant.
In fact, from the above expression,
L
= mrvq.
Finally, we see that the statement of Kepler's second law is that same
as the statement of conservation of angular momentum:
dA/dt = L/2m = constant
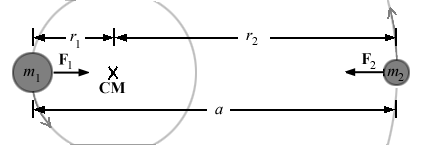
2. Kepler's Third Law
For the general
case of two masses interacting according to Newton's Law of Universal Gravitation,
the two masses actually orbit about the center of mass of the system, not
necessarily the center of the more massive body.
 Recall the equation for center
of mass
Recall the equation for center
of mass
rcm
= Smiri
/
Smi
For a two mass system,
we will refer to the separation of the two masses as a = r1
+ r2,
where r1
is the distance of mass m1
from the center, and r2
is the distance of mass m2
from the center. Consider the case when the two masses are in circular
orbits. During their motion, the two planets must be acted on by
a centripetal force given by
F1
= m1v12/r
= 4p2m1r1
/
P2
and
F2
= m2v22/r
= 4p2m2r2
/
P2
where we have used v
= 2pr / P.
Now, by Newton's third law, these two forces must be equal in magnitude
(and opposite in direction), which means m1r1
=
m2r2
.
This actually proves that the center of the circular motion is the center
of mass. From this and a = r1
+ r2,
we have
r1
= [m2/(m1+
m2)]a.
Also, by Newton's Law of Universal
Gravitation we have the expression for the force:
F1
= F2 = F
= Gm1m2/a2,
so using the expression for
F1,
we have
Gm1m2/a2
= 4p2m1r1
/
P2
= (4p2m1
/
P2)
[m2/(m1+
m2)]
a,
or
P2
= [4p2/G(m1+
m2)]a3
which, as promised, is the expression
corresponding to Kepler's third law.
Note that the center of mass
is also called the barycenter.
The two masses orbit the barycenter with the same period--you use the separation
between the masses, a, not the
distances of the masses r1
and r2
from the center of mass, to determine the period.
3. Orbital Velocity
We will now use
these results to derive a particularly simple equation for the orbital
velocity for any point on an elliptical orbit. Since most
orbits are elliptical, this will be a very useful equation.
We decompose the velocity
into its two components:
| vr
= dr/dt = r' and
vq
= r (dq/dt) = rq' |
Going back to our equation
for an ellipse:
r = a(1 -
e2) / (1
+ e cos q)
we can explicitly take the derivative
and get the radial component of the velocity as
vr
= dr/dt = a(1 -
e2) d/dt [(1
+ e cos q)]-1
= ae(1 -
e2) sin q
dq/dt
/
(1 + e cos
q)2
But note that earlier we had
rvq
= r2dq/dt
= 2pab/P = 2pa2(1
-
e2)1/2/P,
so
dq/dt =
2pa2(1
-
e2)1/2/Pr2
Substitution of
this into the equation for vr,
gives
vr
= ae(1 - e2)
sin q [2pa2(1
-
e2)1/2/Pr2]/
(1 + e cos q)2
= [2pa
/ P(1 - e2)1/2]
(e sin q).
The corresponding perpendicular
component of the velocity is
vq
= r dq/dt = 2pa2(1
-
e2)1/2/Pr
= [2pa
/ P(1 - e2)1/2]
(1 + e cos q).
We simply sum the squares of
these components to get the total magnitude of the velocity
v2
= vr2
+ vq2
= (2pa / P)2
(1 + 2e cos q + e2)
/ (1 - e2).
It is useful to substitute from
the equation of an ellipse for the quantity e cos q:
e cos q
= a(1 - e2)/r
-
1
which gives:
v2
= (2pa / P)2
[(2a/r)(1
-
e2)
+ e2 -
1]
/ (1 - e2)
= (2pa / P)2
(2a/r
-
1).
Finally, from Kepler's third
law, P2
= [4p2/G(m1+
m2)]a3,
we have
v2
= [(4p2a2)
G(m1+
m2)
/ 4p2a3](2a/r-
1)
= G(m1+
m2)
(2/r - 1/a)
This final equation for the
velocity of an elliptical orbit
is called the vis
viva equation.
What have we learned?
We found that Kepler's
second law (Law of Equal Areas), is equivalent to conservation of angular
momentum L = mrvq,
so that dL/dt = 0 for any orbit.
This is a consequence of the central force nature of the gravitational
force--only a perpendicular force could change a bodies' angular momentum, and since there is none, the angular momentum cannot change.
We obtained simple expressions for the speed of a planet or other orbiting
body at perihelion and aphelion:
vperi
= (2pa/P)[(1 +e)/(1 -
e)]1/2
vap
= (2pa/P)[(1
-
e)/(1
+ e)]1/2.
We also noted, using Newton's
third law (Law of equal action and reaction), that two bodies orbit their
combined center of mass (the barycenter) rather than the center
of either body. From this and Newton's Law of Universal Gravitation
(F = Gm1m2/a2),
we proved Kepler's third law in its quantitative form:
P2
= [4p2/G(m1+
m2)]a3.
Applying Kepler's third law,
we were able to obtain a more general equation for orbital speed, valid
at any point in the orbit, the vis viva equation:
v2=G(m1+
m2)
(2/r - 1/a).