B: Orbits and Energy

1. Conservation of Energy

Recall the concepts of potential energy U, and kinetic energy K, the sum of which gives the total energy

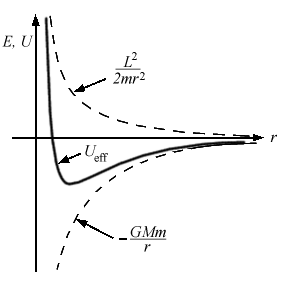
E = K + U

where K = 1/2 mv².  But what is the potential energy appropriate to our planetary system?

Remember that only differences in potential energy are important.  If we raise a mass at the surface of the Earth by a distance h, we do work against gravity
 

		r2
W =			F . dr	= -mgDr = -mgh
		r1

and the negative of this work is the change of potential energy

 

		r2
DU = -W = -			F . dr	= mgh
		r1

Raising a mass from the floor to the desk raises the potential energy by mgh, and raising it by the same height from the desk to a shelf also raises U by mgh -- only the difference DU matters. Thus, we are free to choose our zero of potential energy anywhere we wish.

We will choose DU = 0 at r = infinity, which means the potential energy anywhere in the system is negative.  Now what is the potential energy at position r?  We first place a test mass of mass m at infinity, and then move it radially inward to distance r from the center (from mass M) with the force of gravity acting all the way along this path.  We have
 

		r	GMm
U = -		-		r .dr
		inf	r2

which evaluates to
 

		r	dr		GMm	| r
U = GMm				= -		|
		inf	r2		r	| inf

or finally,

U = -GMm/r         (Gravitational potential energy)

As advertised, the potential energy is negative for any r, and approaches zero as r approached infinity. The total energy for an elliptical orbit, then, is

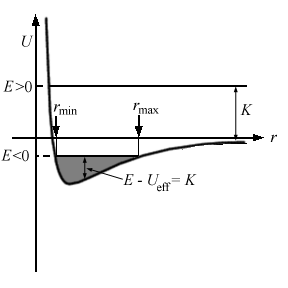
E = K + U = 1/2 mv²- GMm/r
    = 1/2 mG(M+m)[2/r- 1/a] - GMm/r

E = - GMm/2a

where we have used the vis viva equation (which is why this is valid only for elliptical orbits), and we have made the approximation that M >> m.

Note that the total energy is negative, and is just a constant.  Thus, energy is conserved along the orbit, as of course it must be.

Now we will examine the total energy for any orbit, not limited to elliptical orbits.  To do this, we need to use conservation of angular momentum.  It is possible to show, although we will not do so, that the angular momentum and eccentricity are related by

L² / GMm²r = 1 + e cos q,

so solving for r, we get

r = (L² / GMm²) / (1 + e cos q).

Note that this has the same form as the general expression for the polar equation for a conic section.  Let us now repeat the calculation of total energy in the same way as before:

v_r = dr/dt = (L² / GMm²) d/dt [(1 + e cos q)]^-1
    = (L² / GMm²) e sin q dq/dt / (1 + e cos q)²

Recall that |L| = |r x p| = mrv_q, so that rv_q = L/m. But since v_q = r dq/dt, we have r²dq/dt = L / m,  so. Putting this into the above equation,

v_r = (GMm / L) (e sin q).

The corresponding perpendicular component of the velocity is even simpler to derive

v_q = r dq/dt = r²dq/dt / r = L / rm = (GMm / L) (1 + e cos q).

So the total velocity is

v² = v_r² + v_q² = (GMm / L)² (1 + 2e cos q + e²)

and finally the kinetic energy is

K  = 1/2 mv² = 1/2 m(GMm / L)² (1 + 2e cos q + e²)

while the potential energy is

U = -GMm/r = -(GMm)²m/L²(1 + e cos q)
    = -1/2 m(GMm / L)² (2 + 2e cos q)

We finally come to the rather simple expression for total energy, for an orbit of the form of any conic section:

E = K + U = 1/2 m(GMm / L)² (e² - 1)            (Total energy for any orbit)

It is instructive to solve this equation for the eccentricity, to get

e = [1 + 2L²E / (GMm)²m]^1/2

In particular, note that

• for E > 0, we have e > 1 ==> hyperbola
• for E = 0, we have e = 1 ==> parabola
• for E < 0, we have e < 1 ==> ellipse

We can consider the kinetic energy as having a radial part and an angular part:

K  = 1/2 mv² = 1/2 mv_r² + 1/2 mv_q²
K  =                K_r    +     K_q

where v_q² = L² / m²r²    ==>    K_q = 1/2 mv_q² =1/2 L² / mr².  Consider a body moving inward through the solar system.  As r decreases,  the angular kinetic energy increases for smaller r due to conservation of angular momentum.  Since the total energy is conserved, this increasing angular kinetic energy comes in part from the radial kinetic energy.  The system acts as though there were a radial force opposing the inward motion.  Let us write the total energy as

E  =  K_r+ K_q + U(r) = 1/2 mv_r² + 1/2 L² / mr² - GMm/r = K_r+ U_eff

so we call this combination an effective potential.  Graphically, we have: There is a nice way to interpret orbits using this diagram.  Since E = constant on any orbit, if E < 0 we have a bound orbit, with two turning points where K_r= 0,

r_min = r_peri
r_max = r_ap

Note that any orbit with E < 0 has two turning points.  For E = 0, there is only one turning point, and the object reaches infinity with zero energy.  Finally, for E > 0, there is again one turning point, but the object reaches infinity with energy left over.

Effective potential in general relativity (strongly curved space-time).