| Physics 321 |
|
Prof. Dale E. Gary
NJIT |
Note: Some of the images on this page were copied from Nick Strobel's Astronomy Notes web site. The official, updated version is available at his web site. Select this link to go to his web site.
Introduction: Parallax,
Magnitudes, and Color Index
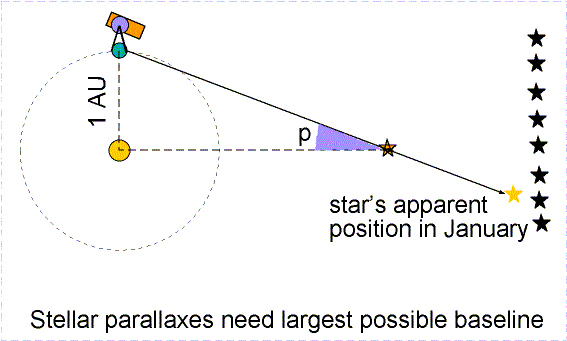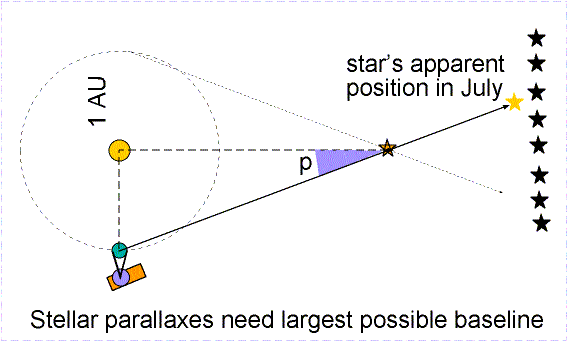
Stellar Parallax:
How far away are the stars?
We hear about the distances to certain stars, gas clouds, even galaxies,
but "how do they really know?" The answer to this question will occupy
us through the entire course, and involves many different clues that, with
painstaking work, can be deciphered and put into a framework, called the
distance
scale. This work is still going on, and is a major
effort in Astronomy. However, the first step in the distance scale
could not be easier to understand. It is the same way that we determine
the distance to a glass of milk or a soccer ball.

The distance to the star is related to the (half) angle (or parallax angle) that the star shifts by:
| 1 AU | 1 | ||||
| d | = |
|
~ |
|
|
| tan p | p |
where the approximation is valid only if the angle is small and is given in radians.
You can show this with a simple calculator exercise. Take the tangent of 1 degree and note that tan p is not equal to p when in degrees. Then convert your 1 degree to radians and take the tangent. The two agree very well.The distance from the Sun to the Earth is 1 AU, or Astronomical Unit. This is a huge distance, 93 million miles, or 150 million kilometers. Even so, the nearest stars shift only a very small amount.

We need a small unit of angular measure. It is convenient to express angles in arcseconds ( " ). One degree can be divided into 60 arcminutes ( ' ), and 1' can be divided into 60", so there are 3600" in 1 degree. Since 1 radian = 57.3 degrees, there are about 206265" in a radian. We can rewrite the above equation as:
| 206265 | |||
| d | = |
|
|
|
|
We define a new unit of distance, the parsec, (parallax second -- pc), equal to 206265 AU = 3.086 x 1016 m, so that we can write the distance in parsecs as simply the inverse of the parallax:
|
Astronomers always use distances in parsecs (pc), or kiloparsecs (kpc), or megaparsecs (Mpc), and sometimes in gigaparsecs (Gpc). You have probably heard of distances given in light-years (ly). The conversion from pc to ly is 3.26 ly = 1 pc. Astronomers never use the distance unit of light years (ly) among themselves, only when talking to the public. The parallax angle, p, is often given by the greek letter p, but to distinguish parallax from the constant p, it is sometimes written p".
The nearest star other than the Sun is Proxima Centauri (Prox Cen), which has a parallax angle of 0.77". What is its distance in pc?2 Modern parallax measurements from the ground have a probable error of 0.004", so we cannot get reliable distances to beyond about 100 pc. From space (e.g. Hipparcos satellite), we can do a little better.
The Magnitude Scale:
It is immediately clear when you look at the stars that some are much brighter than others. Does this mean that the brighter stars are closer, and the dim ones are farther away?3 The brightness that a star seems to have is called its apparent magnitude (m). (Note that here we are using the term brightness incorrectly. We will fix it in a moment.) Astronomers have developed a quantitative measure of apparent magnitude, based on an old scheme suggested by the ancient Greek astronomer Hipparchus.--magnitudes 1 through 6 for the brightest to the dimmest stars visible to the naked eye. Note that the brighter the object, the smaller the magnitude. To use this scheme for even brighter objects (like the Sun) the magnitudes have to go negative (the Sun has an apparent visual magnitude of -26.8). The faintest objects visible to large telescopes are around magnitude 27 or so.
or, finally,log fn/ fm = (m-n)/5 log 100 = 2/5(m-n)
This means that the difference in magnitudes of two stars is 2.5 times the log of the ratio of their energy fluxes. Note the order of the indexes. The flux corresponding to the first magnitude (m) goes in the denominator.
m - n = 2.5 log fn / fm
Example: The star RR Lyrae varies from 7.1 to 7.8 magnitude. What is the change in flux from maximum flux fmax to minimum flux fmin?If flux is the energy / s through a surface (e.g. the pupil of your eye), then the total energy / s from the star must be the flux through a sphere of radius r, where r is the distance to the star. This total energy / s, or power, is called the luminosity (L). Since such a sphere has an area of 4pr2, we have the relationship:m - n = 7.8 - 7.1 = 2.5 log fmax / fminso the star almost doubles in flux!
=> fmax / fmin = 10(0.7/2.5) = 100.18 = 1.91Example: A binary system consists of two stars a and b, with a flux ratio of 2. The magnitude of the two together is +5.0. What is the magnitude of each separately?
|
We can also define an absolute magnitude (M), which is defined as the magnitude a star would have if it were at a distance of 10 pc. With this definition, we can, for example, compare the intrinsic brightness of two stars. From the magnitude equation, above, we can compare the magnitude m2 of a star at a distance d, with its magnitude m1 at a distance of 10 pc, by:
but since by definition M = m1, we can set m2= m to get:m2 - m1= 2.5 log f1/ f2 = 2.5 log (d / 10 pc)2 = 5.0 log (d / 10 pc)
| m - M = 5 log (d / 10 pc) |
The quantity m - M is called the distance modulus. The larger the distance modulus, the farther the star is away from us. How far is the star away from us if its distance modulus is zero?4
Brightness vs Flux:
In the discussion above, we used the term brightness when discussing stellar magnitudes, and this is a natural use of the term in everyday English language. However, the physical quantity we really mean is energy flux, or simply flux. A more precise use of the term brightness actually refers to a different physical quantity, better called the surface brightness or specific intensity. We will define and discuss this in more detail next week. However, let us discuss the difference now.
Consider a piece of paper lying on the lawn at night, illuminated by the light from a nearby window, where the room lights are on. The brightness of the paper depends on the flux of light energy from the window. Now we will turn out the room lights and turn on a flashlight, shining through the window, such that the brightness of the paper does not change. In the two cases, the same flux of energy is falling on the paper, yet if we were to place our eye near the paper and look at the light source, which would be brighter?

Because the flux of energy falling on the paper must be the same in the two cases, we can think of the situation as follows: All of the light from the window, in the first case, would be concentrated into the much smaller area of the flashlight beam in the second case. From the discussion of magnitudes above, we would say that the window and the flashlight have the same magnitude because the flux is the same at the distance of the paper, yet clearly the flashlight would appear brighter (the surface brightness is greater). So you see that surface brightness is not the same as flux, or magnitude.
To make this clearer, consider the brightness of the Sun as seen from different planets. From the Earth, the Sun has an angular diameter of about 1/2 degree. If we look at a tiny portion of the surface, say a 1" (1 arcsecond) square area, we will measure a certain brightness. From Jupiter, at a distance of 5.2 AU from the Sun, however, the Sun has an angular diameter of 1/2 degree/5.2 ~ 0.1 degree. Its flux, and so its magnitude, will be correspondingly smaller, yet if we again look at a 1" square portion of the surface we find that it has the same brightness! Surface brightness, like luminosity, is intrinsic, meaning it does not change just because we are near or far from it. Flux, or magnitude, in contrast, does depend on how far away we are. We wil discuss these issues in more mathematical terms next week.
You might ask why we loosely talk about brightness of stars in everyday language, when we really mean flux. Consider what happens when we move ever farther from the Sun. Its angular diameter gets smaller and smaller, yet its brightness does not change. But what happens when it is smaller than our 1" square area? If we define brightness as the flux through that 1" square area, we see that as the Sun gets ever smaller, the brightness will go down (because the surface is no longer resolved). Stars are so far away that we cannot usually resolve them, and in this situation the brightness defined in this way does change with distance exactly the same way as the flux. This is the reason we can get away with not distiguishing between flux and brightness for stars.
Answers:
1. Use
the Earth's orbital motion around the Sun.
2. 1
/ 0.77" = 1.3 pc
3.
Not necessarily. Some of the nearer stars are the faintest.
This is because they have a low intrinsic brightness.
4. 10
pc