Star Formation

Basic Picture
 

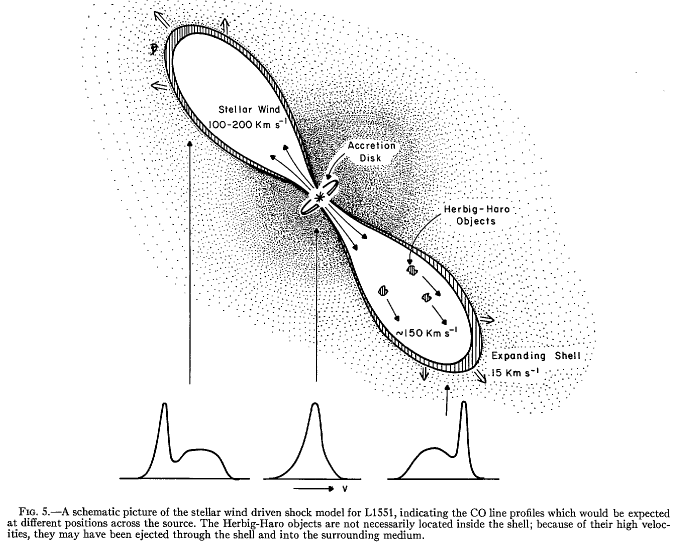
Clouds of gas and dust collapse and form Young Stellar Objects (YSOs), sometimes visible and sometimes enshrouded in dust.  The relevant physics of the collapse includes

• Size scale for collapse: L ~ 10⁷ (T/r)^1/2~ 0.1 pc for T = 10 K, r = 10^-15 kg m^-3
This estimate comes from applying the virial theorem, which if you will recall says that half the potential energy difference between two equilibrium states of a system is available to be (and must be) radiated away, and the other half goes into internal heating of the system.  The thermal energy is
E_thermal = NkT
while the potential energy of a spherical distribution of mass is
U = -GMm/R = GM²/L
where we equate the radius R with the length scale L for the system.  We can roughly relate the total number of particles in the cloud, N, with the mass of the cloud by considering that all of the particles are all hydrogen molecules (the cloud is very cold, so we do not consider individual atoms): N = M/2m_H.  Then equating E = -U/2, we have kT/2m_H~ GM/L.  Writing this in terms of the density of the cloud, r = M/(4/3pL³), we have the final result L ~ (kT/m_HGr)^1/2 = 10⁷ (T/r)^1/2.
• Time scale for (free-fall) collapse: t_ff = 6.4 x 10⁴ r^-1/2~ 10⁵ yr for r = 10^-15 kg m^-3
Free fall means that the particles are in orbit around their common center of mass, and do not collide, but fall freely.  We can estimate how long it will take for a particle to fall from the edge of the cloud by taking 1/2 of its Keplerian orbital period, assuming that it falls directly in, so that the semi-major axis of the orbit ellipse is a = r/2, where r is the radius of the cloud.  From Kepler's third law,
P = [(4p²/GM) a³]^1/2 = 2t_ff .
Again relating the mass to the density, as we did above, and using this value for the semi-major axis, we have:
t_ff = (3p/32Gr)^1/2 = 6.4 x 10⁴ r^-1/2
Of course, the collapse will only proceed until collisions do become important.  Then the collapse will slow, and the object will begin to heat up.  We will look at this in more detail shortly.
• Angular momentum: m_i v_i r_i = m_f v_f r_f => v_f = v_i ( r_i/r_f ) = 1 m/s (10¹⁵ m/10⁹ m) ~ 1000 km s^-1
Conservation of angular momentum, the same law that causes a skater to spin faster as they pull their arms closer to their body, causes the collapsing cloud to spin faster as it gets smaller.  Even for very slowly spinning clouds initially, the vast change in radius as the cloud collapses to a stellar-sized object leaves the object with enormous spin velocity.  We can estimate this final velocity very simply by equating the initial angular momentum (l_i = m_i v_i r_i) to the final angular momentum as above.  Thus, the object spins up by a factor of 1 million as its radius drops by the same factor.
• Magnetic fields: conservation of magnetic flux (magnetic field strength / unit area) F = pr ² B => B_f = B_i ( r_i/r_f )² ~ 100 T forB_i = 0.1 nT.
Under the conditions of the collapsing cloud, another quantity is conserved--the magnetic flux.  The increase in magnetic flux is even greater than that for spin, because it depends on the square of the radius.

Thus, we can expect a cloud of typical size 0.1 pc to collapse over perhaps 1 million years, and when it reaches stellar size it should be spinning very rapidly and be highly magnetized.  This is exactly what is observed, except that the spin rate and magnetic field strength are somewhat less than predicted by these simple arguments.  Our best understanding of the reason for the discrepancy is that the strong magnetic fields themselves slow down the rotation rate by coupling the spinning core to the outer disk, and dynamical processes cause the proto-stellar object to shed some of its mass and much of its magnetic field.

• O,B Associations
• stellar disks

• protoplanetary disks
• beta pic