Pulsars
| Physics 321 |
|
Prof. Dale E. Gary
NJIT |
Star Deaths
Mass, and type of Stellar
Corpse
Main sequence stars with M < 7 Mo end up as white dwarfs:
|
|
=> He white dwarf |
| (0.5 - 5 Mo) | => Carbon/Oxygen white dwarf |
| (5 -7 Mo) | => Oxygen/Neon/Magnesium white dwarf |
Physical Structure
P = Kr5/3 (K = constant) does not depend on temperaturein contrast to ideal gas P = nkT.
The more massive a white dwarf, the smaller its radius.
R = 4pK / [G(4/3p)5/3M 1/3]Cooling: No nuclear engine, so they cool off with timescale
tcool ~ L-5/7until they become a black dwarf. Typical lifetime is several billion years to cool to a black dwarf.
Observations
Sirius B has luminosity L = 3 x 10-3 Lsun, and a temperature of T ~ 29,000 K. What is its radius? From L = 4pR2sT4, R can be found to be 7 x 10-3 Rsun. Typical sizes are 0.01 Rsun, which is about the radius of Earth.
White dwarfs have spectra
in three classes
| DA | "A-star" type spectra (lines of H Balmer series) |
| DB | "B-star" type spectra (lines of He) |
| DC | "C" = continuum spectra (no lines at all) |
But the interiors are all the same--degenerate He, C, or O-Ne.
Gravitational Redshift
Photons lose energy in "climbing out of" a gravitational well (like the surface of a white dwarf). Energy of photon at surface of star is Ki + Ui while energy at infinity is just Kf. (since Uf = 0 at infinity). Conservation of energy gives DK = Kf - Ki = Ui = -GmM/R, which is the change in energy of the photon hDn. Thus
h Dn = -GmM/R.Now the "mass" of photon can be determined from E = mc2 = hn. => m = hn/c2, so we have
Dn = -GMn/Rc2. or the relative shift is Dn / n = -GM/Rc2This is negative because the photon loses energy and shifts to smaller frequencies, longer wavelengths. The corresponding wavelength shift is positive
Dl / l = GM/Rc2. Gravitational Redshift (non-relativistic)This is an approximation correct for weak gravitational fields. Stronger fields require a more exact expression correct for general relativity:
lf/ li = [1 - 2GM/Rc2]-1/2 Gravitational Redshift (relativistic)This shift is combined with doppler shifts, so must use binary systems where doppler shifts are accurately known, to test. For Sirius B, best measurement is Dl / l ~ 3 x 10-4 compared to theoretically exact value 2.8 x 10-4.
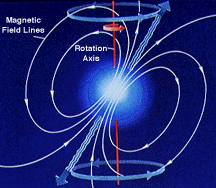
Magnetic White Dwarfs
B ~ 104 T are seen in a few percent of white dwarfs, especially those in binary systems, due to enhancement as star collapses (conservation of magnetic flux, as we saw during the collapse of protostars).
Brown Dwarfs
Objects with mass in the range 0.002 < M/Mo < 0.08 never make it to the nuclear burning stage and simply cool off (like white dwarfs) as they age. Below 0.002 Mo, objects are rather arbitrarily defined as a planet.
Neutron Stars
When a star's mass at the end of its life is M > 1.4 Mo, electron degeneracy is no longer enough to keep gravity at bay, and matter is crushed to force inverse b decay
p+ + e- ---> n + n.so the protons and electrons are combined to form neutrons--a neutron star. The state of matter is a neutron degenerate gas, with same equation of state as for electron degeneracy, although constant K is different. As before, objects with greater M have smaller radii, up to ~ 3 Mo. Radii are typically 10-30 km. Gravitational redshift is now up to Dl / l ~ GM/Rc2 ~ 0.2.
Pulsars

You can imagine the forces on the fastest pulsar. The surface speed is v = 2pR / P, where P is the pulsar period and R is the pulsar radius (about 10 km = 104 m):
v = 2pR / P = 2p(104 m) / 0.0016 s = 3.9 x 107 m > 0.1 c.Its centripetal acceleration is ac = v2/R, and the star will rip itself apart if this is greater than the gravitational acceleration holding the star together, ag = GM / R2, that is, if the surface velocity v is greater than v = [GM/R]1/2. What is the smallest possible period P that a pulsar could have?
P = 2pR / v = 2pR / [GM/R]1/2 = 0.3 msWe can combine mass and radius and write this in terms of only one quantity, the density, as
P = 3.8 x 105 r-1/2.With the fastest periods of about 2 ms, one can see that the density must be high.
The Supernova Connection
Pulsars are continually slowing down, unless kept rotating by additional energy input from a binary companion. Where does the energy go? We can show that the energy loss indicated by slowdown of the Crab Pulsar is about that needed to keep the Crab Nebula energized.
The Crab pulsar rotation period is P = 0.03 s, and its spin-down rate is dP/dt ~ 4 x 10-13 s/s, or ~ 10-5 s/yr. The rotational energy is just
Erot = 1/2 I w2,where w = 2p/P is the angular rotation rate and I = 2/5 MR2 is the rotational inertia of a sphere. The energy loss is dErot/dt. What we will do is equate to luminosity of the nebula, so L = -dErot/dt.
dErot/dt = 1/2(2/5 MR2)d/dt[2p/P]2 = (4p2/5) MR2 d/dt(P-2)Solving for rate of change of period,
= -(8p2/5) MR2P-3 dP/dt = -L
dP/dt = (5/8p2) LP3/MR2Plugging in some numbers (you will do this for a homework problem) gives a value close to the observed spin-down rate.
How does this transfer of energy happen? The cause of the spin-down is magnetic torque due to the strong fields threading from the star through the nebula. Somehow this magnetic energy is being converted to high-energy particles and radiation from the nebula.
