Gravity in a Close Binary System

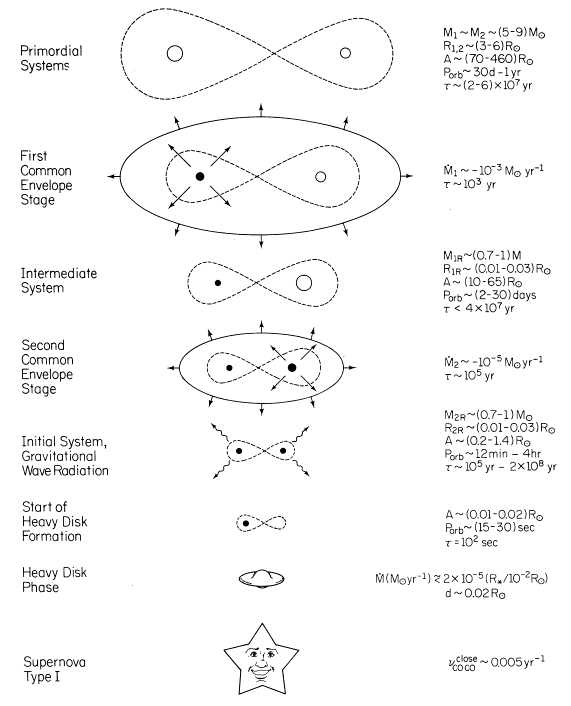
At least half of all stars in the sky are actually multiple star systems, with two or more stars in orbit about their common center of mass.  In this lecture we will be concerned with systems that are close enough to significantly interact over their lifetimes.  Generally, such stars will exert a tidal influence on each other, causing internal motions in the stars that dissipates orbital and rotational energy until the two are tidally locked, always facing each other.  In this situation, the system rotates rigidly in space, and although the stars may be distorted, they are no longer losing energy due to the tidal interation.

To think about the environment near these stars, consider a "test" mass, also rotating rigidly with the system.  Placing the center of mass of the system at the origin, the small mass will feel the gravitation force from both stars, and also the fictitious "centrifugal force" due to its own rotation with the system

F_c = mw²r

Rather than work with forces, we will consider things from the point of view of potential energy (recall that F = -dU/dr), so the fictitious centrifugal force on the mass is

 

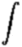Uc = -		mw2rdr =		-1/2 mw2r 2.

Thus, the total potential energy in this rotating frame, shown in the figure below, is the gravitational potential energy plus the centrifugal potential energy, or

U = - GM₁m/s₁- GM₂m/s₂- 1/2 mw²r ².

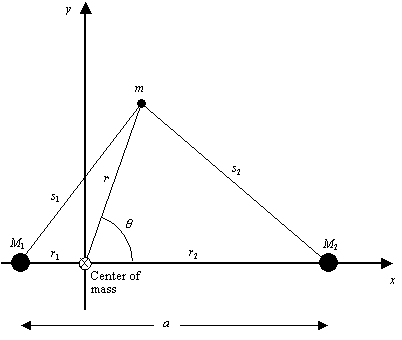
Corotating coordinates for a binary star system

For convenience, we can write this as an effective potential energy per unit mass, F, [erg / g]

F = - G(M₁/s₁- M₂/s₂)- 1/2w²r ².

Note that the distances s₁ and s₂ can be written in terms of r₁ and r₂ through the law of cosines, and the angular frequency of the orbit comes from Kepler's third law for the orbital period

w² = (2p/P)² = G(M₁ +M₂)/a³. = G(M₁ +M₂)/(r₁+r₂)³.

Finally, from the definition of the center of mass, we have

M₁r₁ = M₂r₂

Combining all of these expressions allows us to evaluate the effective gravitational potential at every point in the orbital plane of the binary star system.  Figures 17.2 and 17.3 show the results, from which we can see the shape of the equipotential surfaces (Fig. 17.3) and understand the locations and importance of the Lagrangian points, especially the inner Lagrangian point, L₁. Further discussion, with pictures.

 
 
 

Table of Classes of Cataclysmic Variable Stars
(from Zeilik & Gregory--Intoductory Astronomy & Astrophysics)

Dwarf Novae

This class of outburst in brightness is thought to be due to quasi-periodic brightenings in the accretion disk around a white dwarf.  During quiescent periods, the mass loss rate from the inflated secondary star is about 10^-10 solar masses per year.  Episodically, the mass transfer from the secondary goes up by a factor of 100, to 10^-8 solar masses per year. SS Cygni is a prototype of this kind of system.

In this type of outburst, it is the matter actually falling onto the primary white dwarf that powers the explosion.  It requires a mass transfer rate of about 10^-9-10^-8 solar masses per year, which over 10⁴-10⁵ y accumulates in a layer on the surface of the white dwarf in the form of hydrogen rich electron-degenerate matter.  This layer eventually reaches a temperature of a few million degrees, and with the help of CNO from the white dwarf, initiates run-away nucear burning that causes much of this outer atmosphere to expand into a shell.  The nova outbursts come in two types, fast and slow.  Both have an equally rapid rise, but fast novae are within 2 magnitudes of maximum brightness for only a week or two, while slow novae may take nearly 100 days for a similar decline in brightness.  About 2-3 are seen in our galaxy every year, but about 30 are seen in the Andromeda Galaxy each year, so most of those occuring in our galaxy are probably obscured by intervening dust.  The speed of ejection can be measured from doppler shifts during the outburst, and later the expanding nebula can be used to determine the distance to the nova (recall that transverse velocity is related to proper motion and distance by v_t = 4.74m" d_pc).

There are two basic types of supernovae, classified according to observational characteristics of their spectra near maximum brightness.  Those that show no strong hydrogen lines are Type I, those that do show strong hydrogen lines are Type II.  One type is the result of core collapse in a giant star, while the other involves a white dwarf in a close binary system.  (Can you identify which is which?)

A recent, famous Type II supernova was Supernova 1987A for which we can look at detailed timing of events.  Type II supernovae are responsible for all of the elements heavier than iron in the universe, through nucleosynthesis.

There are two models for Type I supernovae, although our text prefers the first scenario:

• A carbon-core white dwarf accretes matter from a companion until it reaches around 1.3 solar masses.
• At that mass, the core suddenly reaches sufficient pressure to begin fusing C into heaver elements.
• Just as in the Helium flash, the degenerate C cannot expand as temperature goes up, so there is a complete conflagration of the core until the degeneracy is explosively broken and the star releases such energy that it is completely destroyed.

The second scenario starts the same as the first, but the mass eventually exceeds the Chandrasekhar Limit of 1.4 solar masses.

Type I supernovae are subdivided into three classes, Type Ia,b, and c, depending on the presence of certain spectral lines (Si, He).  Type Ia supernovae are the "cleanest" and have remarkably constant peak brightness at a whopping -20 absolute magnitude.  Because of this, they can be used, when seen in distant galaxies, to determine the distances to these galaxies.  This is a critical observation, since it allow us to calibrate one of our distance scale measurements, the redshift of galaxies, which we will show later implies that the universe is expanding.