Counting Stars

It is a significant problem to determine the shape and extent of our galaxy from our point of view inside it.  On a clear night with a dark sky, the band of stars and dust that make up the Milky Way can be easily seen, but when mapped over the whole sky in optical light, it has a complicated appearance that does not represent its real shape.

The first attempts to determine the shape of our galaxy, called the Milky Way Galaxy were through simply counting stars.  Sir William Herschel made the first systematic star count in the 1780's, later expanded by Jacobus Kapteyn the early 1920's.  Both of these attempts ignored interstellar extinction (the dimming of starlight by dust), and concluded that the Sun resides near the center of a flat, pancake-shaped distribution of stars.

However, between 1915 and 1919, Harlow Shapley estimated the distances to globular clusters, using RR Lyrae and Pop II Cepheid variables as distance indicators.  He found that many more clusters where seen in the direction of Sagittarius, and concluded that globular clusters are distributed uniformly around our galaxy.  The concentration in the direction of Sagittarius was due to the fact that our Sun is off-center within the galaxy, and the center is in the direction of Sagittarius.

We can now obtain images in the infra-red region of the spectrum, which can penetrate dust easily.  When we image the entire sky in the infra-red, as was done with the COBE satellite, we obtain the much clearer picture of the Milky Way Galaxy shown below.

Image of the Milky Way Galaxy taken with the COBE satellite. Note that now we can see through the dust to the central bulge, and the disk appears much more uniform.  Below are several views of the Milky Way seen in various wavelengths.

Below is a figure that gives an overview of the structure of our galaxy.  We will be discussing different aspects of this figure in the next several lectures, but for now let's consider only the three main regions.

• Most of the stars of the galaxy reside in a disk, which closely resembles the disks of spiral galaxies seen elsewhere in the sky.  Also in the disk are gas clouds, dust, and very young stars (O-B associations).  The stars tend to have high metallicity (Z > 0.01).
• There is a central bulge of stars near the center of the galaxy that is more spherical in shape.  The stars here are older (and redder) than the disk population.
• Globular clusters are distributed in an approximately spherical halo above, below, and within the disk.  A small number of high-velocity stars are also seen in this halo region.  The stars here are very old, and typically have low metallicity (Z < 0.001)

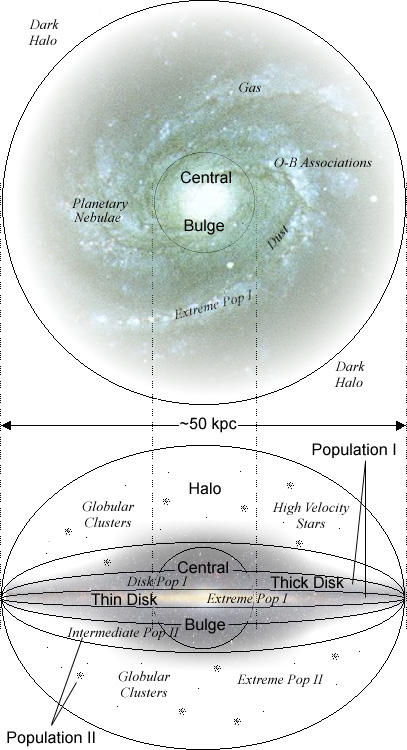
Schematic view of the Milky Way Galaxy.  The top figure shows a "top view" showing the spiral structure as seen from above.  The bottom figure shows an "edge-on view" as seen from the side. (The top view image is of the spiral galaxy M100.  The side view shows the COBE image from the previous figure.)

In addition to these visible features, there is indirect evidence of another source of matter, called dark matter, which lies in a large halo extending far outside the visible confines of the galaxy.  This makes up the dark halo.  The evidence for this enigmatic matter comes from studies of the kinematics, or motions, of the constituents of the galaxy.

As always in astronomy, the building blocks of great discoveries such as galactic rotation and the presence of dark matter come from very basic, simple measurements such as the motions of stars.  As we have seen, a star's speed is measured in two components:

• radial velocity (from doppler shifts of spectral lines) and
• tangential velocity (from proper motion).

Star catalogs such as the Nearby Stars catalog give these measurements for each star.

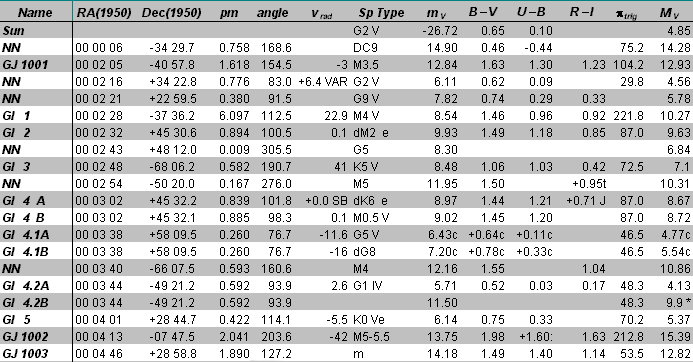
Here, the proper motion (pm, or m") is given in arcseconds per year.  In these units, the tangential velocity of the star, in km/s, is

v_q = 4.74 m"d_pc = 4.74 m"/p"   (km/s)

where p" is the trigonometric parallax, in arcsec.

Example: For star Gl 4.2A, above, we have m"= 0.592 and p"= 0.0483, so v_q = 58.1 km/s.  The radial velocity is shown in the table to be v_r = 2.6 km/s, so the total velocity, or space velocity is v= (v_r²+ v_q²)^1/2 = 58.2 km/s.

The quantities in the table, however, are not so simple to measure.  To convert proper motion to velocity, one must know the distance, which means either measuring a trigonometric parallax (which is impossible for all but the nearest stars) or using a spectroscopic parallax.  In addition, the proper motion must be measured.  For nearby stars, the proper motion can be quite large, but for distant stars it can be very small.  Luckily, we can monitor stars over many decades, after which the proper motion accumulates and can be measured.

Radial velocity is easier, since it is determined from spectral line shifts, which can be seen at any distance (as long as the star is bright enough).  However, for both radial velocity and proper motion one must subtract other motions such as the Earth around the Sun (~30 km/s), and the Sun's own motion through space (~19.5 km/s--our text gives 16.5 km/s).

We learned in the second lecture that stars are assigned right ascension (a) and declination (d) coordinates depending on their positions on the celestial sphere--the extension of the Earth's equator and poles into the sky.  However, it is often more convenient when discussing the kinematics of the galaxy to change to a new coordinate system based on the shape and orientation of the galaxy (the Milky Way) in the sky.

Before we can go further with stellar motions, we need to define a coordinate system in which to make our measurements.  Since we expect the galaxy to rotate about its center, and all of the objects that make up the galaxy should orbit this center in Keplerian orbits, we could form a coordinate system that is galactocentric, and for some cases that is the appropriate system to use.  However, since we are observing from our location in the galaxy, a second coordinate system centered on the Sun will prove more useful.  This coordinate system is called simply galactic coordinates.  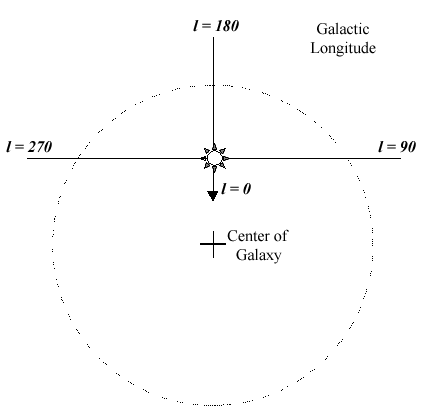As viewed from the Sun, coordinates in the galactic plane are at galactic latitude b = 0^o, while at the galactic poles (N or S), the galactic latitude is b = 90^o.  Galactic longitude l is measured from the center of the galaxy (the Sagittarius region) as shown in the figure below.



The transformations between celestial (a, d) and galactic (l, b) coordinates are:

cos b cos (l - 33^o) = cos d cos (a - 282.25^o)
cos b sin (l - 33^o) = cos d sin (a - 282.25^o) cos 62.6^o + sin d sin 62.6^o     (from celestial to galactic)
                    sin b = sin d cos 62.6^o- cos d sin (a- 282.25^o) sin 62.6^o

                          sin d = cos b sin (l - 33^o) sin 62.6^o+ sin b cos 62.6^o
cos d sin (a - 282.25^o) = cos b sin (l- 33^o) cos 62.6^o- sin b sin 62.6^o   (from galactic to celestial)
 

A graphical representation of these two coordinate systems is shown below:
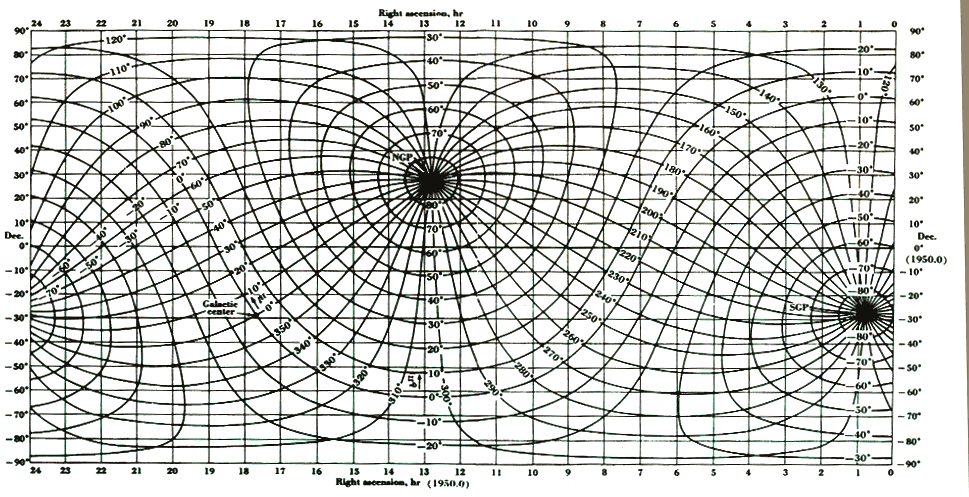Chart for conversion of celestial coordinates to galactic coordinates.  From Kraus, Radio Astronomy, Second Edition, Cygnus-Quasar Books, 1986.

We define the kinematics of the system in terms of the rotational motion, about the galactic center, of all of the stars in the solar neighborhood.  This allows the Sun to have a motion with respect to this average rotational motion.  Assumptions that go into the model are:

• Stars share the general rotation of the galaxy.
• Stars have their own peculiar motions superimposed on this general rotation.
• The average velocity (magnitude and direction) of stars in the local solar neighborhood should be zero with respect to this general rotation.
• The Sun may have a motion relative to the general rotation.
Thus, if we examine all the motions of stars in the very local solar neighborhood, and their velocities do not average to zero, any residual velocity must be due to the Sun's own motion (due to the fact that the Sun's orbit around the galactic center is not perfectly circular).  In fact, stars should (statistically) show a diverging pattern in the direction our Sun is traveling, called the solar apex, and show a converging pattern in the opposite direction (the solar antapex).  Once the apex and antapex are found, we determine the Sun's peculiar velocity by averaging the radial velocities in these directions.  The solar apex is in the direction toward l = 53^o, b = 25^o, a point in the constellation Hercules.

These considerations allow us to define a Local Standard of Rest (LSR).  Stars moving about the galactic center in perfectly circular orbits would be expected to have zero velocity in this LSR frame.

The other coordinate system, centered on the center of the galaxy, has coordinates R, q, and z, corresponding to radial distance from the center, azimuthal angle, and distance out of the plane.  The corresponding velocity components are defined as P = dR/dt, Q = R dq/dt, and Z = dz/dt.  The rotation rate at the radius of the Sun gives for the LSR velocity: P_LSR = 0, Q_LSR = Q_o, and Z_LSR = 0, where Q_o is the rotation rate at the radius of the Sun.  Peculiar velocities are then defined as

u = P - P_LSR = P
v = Q - Q_LSR = Q -Q_o
w = Z -Z_LSR = Z
Plotting the peculiar velocities as u vs v, gives the diagram of Figure 22.23 of the text.  Note the different velocity dispersion of different types of stellar populations.  Young stars show little dispersion, so are rotating along with the general galactic rotation.  Older stars show a great deal of dispersionn, up to 200-300 km/s difference.  Note the velocity-metallicity relation, in which low-metallicity stars have high peculiar velocities while high-metallicity stars have low peculiar velocities.

We mentioned before that the stars should orbit the galaxy in Keplerian orbits.  For Keplerian orbits, we expect Kepler's Third Law to hold:
 
P² = (4p²/GM)R³
where P is the orbital period, M is the mass interior to the orbit, and R is the radius of the orbit.  For a circular orbit, the period is related to the speed by
 
P = 2pR / V


so the speed V is
 

V = (GM/R)^1/2 ~ R^-1/2.                                      (1)


This is the way that velocity should fall off with radius as long as all of the mass is interior to the orbits being considered.  In contrast, imagine a spherical distribution of mass of uniform density, in which particles (stars!) orbit inside the mass distribution.  The mass interior to the orbit is then
 

M(R) = 4pR³r/3


and the equation above becomes
 

V = (GM(R)/R)^1/2 = G(4pR²r/3)^1/2 ~ R.             (2)
Clearly, the way that the mass is distributed in a galaxy will make a big difference in the velocities of the stars within it.  On the other hand, if we can measure the velocities of stars as a function of radius (the galactic rotation curve), we can determine the mass distribution in the galaxy.

If the speed of orbit of stars depends on radius, then stars far from the solar neighborhood will not be rotating with the LSR.  If equation (1) is valid, stars interior to the Sun's orbit will rotate faster, while if (2) is valid they will rotate slower.