From studies of the motions of stars, the best estimates for the location and orbital velocity of the Sun about the galactic center are:

R_o = 8.5 kpc
Q_o = 220 km/s

In addition to studying the motions of stars, we can use observations of other types of objects to help determine the structure of the galaxy.  For example, the distribution of gas and dust may be different from the distribution for stars.

Recall that the hyperfine splitting (electron spin-flip) of the hydrogen ground state can be studied at the characteristic wavelength of photons emitted--21 cm in the radio part of the spectrum.  This emission is very optically thin, but there are so many H I atoms (neutral hydrogen) that the emission line can be seen everywhere in the galaxy--there is very little obscuration.  This is a prime method for delineating spiral structure in our galaxy.  If we know the rotation curve for the galaxy and assume that the gas is in circular orbit around the galactic center, we can use 21-cm line profiles to map the spiral arms.

Here is how it works:  Along a given line of sight, say there are four clouds A, B, C, and D.  Each is in its own orbit around the galaxy, and so has a different radial velocity, so what would be a single line is split into several components as shown above.  Note that the highest velocity peak is the one that lies closest to the center of the galaxy along that line of sight, which is the distance R_min.  From different lines of sight, we build up maps of spiral arms.  Note that the spiral structure is poorly determined towards l = 0, 180 (why?).

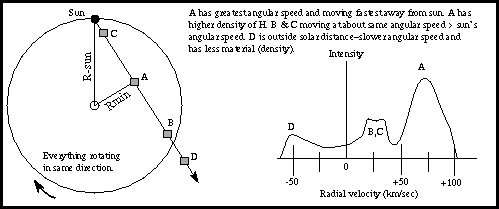
A has the greatest angular speed and is moving fastest away from the Sun.  A has higher density of hydrogen, so appears with the highest intensity. B and C are moving at about the same angular speed, greater than the Sun's angular speed.  D is outside the solar distance, so has slower angular speed, and also has the lowest hydrogen density. (This image is from Nick Strobel's web site.)

We already saw that the distribution of H I is different from molecular clouds (e.g. CO).  Note that CO is a proxy for H₂ (molecular hydrogen), meaning that these two constituents are found together and so are distributed in the same way.  From measurements of CO we find that the inner galaxy is mostly H₂ while the outer galaxy (R > 8.5 kpc) is mostly atomic H.

From our studies of the motions of stars, gas clouds, and other objects, we can develop the rotation curve for the galaxy.   Below are measurements of the rotation curve from CO, H I, and H II regions.  Why do you think the measurements get so uncertain beyond about 8 kpc?

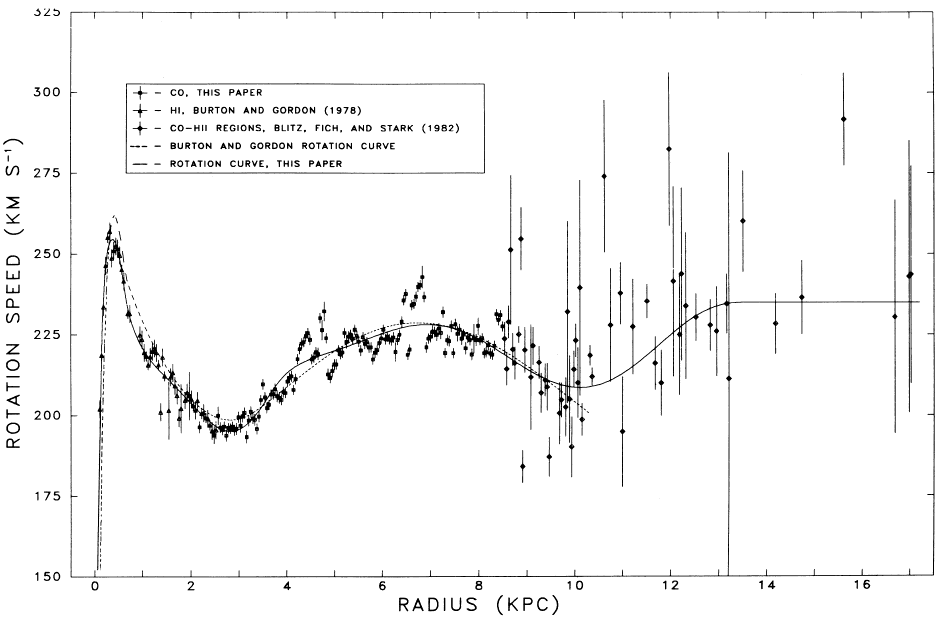
The rotation curve of the Milky Way Galaxy.  The IAU standard values of R_o = 8.5 kpc and Q_o = 220 km/s have been assumed.  (Figure reproduced from Clemens (1985), Ap. J. 295, 422.)

The contributions to the overall rotation curve are shown in the figure below.  The top curve at left shows the total rotation curve.  It has contributions from the spherical galactic bulge and the disk, but these contributions do not make up the entire curve, so another contribution called the corona must exist.  The corona is not evident in anything we can see, so-called luminous matter, so it must be due to some form of dark matter.

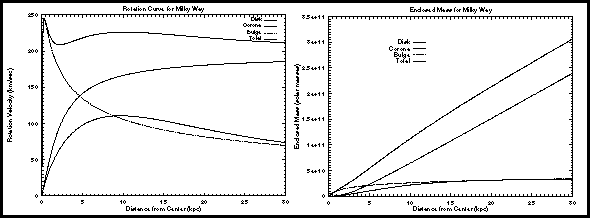
The plot on the left shows the Total rotation curve for our galaxy, made up of contributions from the Bulge, the Disk, and the Corona.  The plot on the right shows the Interior Mass, M(R), as a function of radius (called the enclosed mass here).  Both the disk and the bulge reach a constant interior mass, meaning that at a radius of 25 kpc or so, all of the mass is inside this radius, and the rotation curve for these components drops approximately as R^-1/2.  The corona mass (dark matter), however, appears to continue to rise with radius!  (This image is from Nick Strobel's web site.)

What is this dark matter?  We only know that it exists from its gravitational influence, so some possibilities are:

• gas    (no, should see absorption or emission lines of stars shining through it)
• dust    (no, dust causes extinction of starlight, and glows in the IR)
• MACHOs--Massive, compact halo objects? (e.g. small, faint stars such as black dwarfs [dead white dwarfs], brown dwarfs [failed stars], neutron stars, or black holes)?
• WIMPs--Weakly interacting massive particles? (e.g. neutrinos, or some as-yet-undiscovered particle)?

We can estimate how the density of either MACHOs or WIMPs might fall off from the center of our galaxy.  Assume they exist in a spherical halo (not just in a disk shape).  To cause a constant rotational velocity v_o, say, we must have acceleration due to gravity equal to the required centripetal acceleration

GM(r)/r² = v_o²/r

or

M(r) = rv_o²/G.                                    (1)

So the interior mass must increase proportional to r.  The mass of a thin spherical shell is

dM(r) = 4pr²r(r) dr   =>  dM(r)/dr = 4pr²r(r)

but taking the derivative of (1) wrt r gives

dM(r)/dr = v_o²/G,

so the density required for constant rotational velocity is

r(r) = v_o²/4pr²G.

This means that if the density falls off by r^-2, the interior mass will grow with radius (because the volume increases by r³), and we would expect a constant rotational velocity with radius.

Note that galactic rotation curves are even easier to measure in other galaxies, and they all show this same tendency for a dark matter halo.  We will see that the dark matter problem only continues to get more extreme as we consider larger scale structures of the universe.

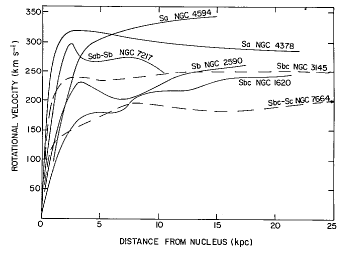
A series of rotation curves for spiral galaxies. (Figure from Rubin, Ford, and Thonnard (1978), Ap. J. Lett., 225, L107.)

Spiral Structure

When we map the locations of neutral hydrogen clouds using the technique of interpreting line profiles, as discussed above, we find that the gas clouds tend to be distributed in clumps.  When these clumps are mapped as a function of galactic longitude and distance (assuming a rotation curve for the galaxy) we find that they lie along discrete spiral arms.  From this we learn that our galaxy is a spiral galaxy, similar to the Andromeda galaxy, or the M100 galaxy shown below.

Because the galactic center region is by definition at galactic longitude l = 0, one would predict small radial velocities in that direction.  However, we find high velocities (in all directions--peculiar velocities) that have a rather large non-zero mean velocity of about -50 km/s (approaching).  This has been called the 3 kpc arm, or expanding arm.  Recent observations indicate that beyond the galactic center region there is a similar motion of stars away from us, as if the stars are making very non-circular orbits in a structure called a bar.  We will discuss this bar structure in the next lecture, when we discuss other galaxies.  The velocities in the inner 2 pc of the galactic core are so high that the derived interior mass function indicates the presence of several million solar masses within the inner 0.5 pc of our galaxy.  A radio source known as Sagittarius A (Sgr A) lies very close to the center, and shows gas velocities of 260 km/s.  If this is an orbital velocity, Sgr A can only be a supermassive black hole.  It is nearly invisible from our vantage point, seen through massive amounts of dust, but in the IR the luminosity in the region is 10⁷L_sun.

In addition to the hydrogen clouds seen in the spiral arms of the disk of the galaxy, there are high velocity clouds seen well out of the plane of the galaxy (b > 10^o).  Nearly all show (negative) velocities of approach.  They seem to be associated with satellite galaxies of the Milky Way, the Large Magellenic Cloud (LMC) and the Small Magellenic Cloud (SMC).  The model for their existence is that they are clouds being pulled from these satellite galaxies in a structure called the Magellenic Stream, due to tidal interactions between those galaxies and ours.