| I | = | I(n)dn (units energy / m2 / s / sr) |
| Physics 321 |
|
Prof. Dale E. Gary
NJIT |
Intensity vs. Flux
The monochromatic intensity I(n) has units of energy / m2 / s / Hz / sr, where sr = sterradians is the unit of solid angle, DW. The intensity, or surface brightness, is then
| I | = | I(n)dn (units energy / m2 / s / sr) |
Integrate this over angular area to get the flux F:
| F | = | I dW (units energy / m2 / s) |
The total amount of power (energy / s) emitted by a star is called its luminosity L, and is just the flux integrated over the area of the star:
| L | = | I(n)dn dW dA (units energy / s) |
| = | 4pR*2 | I dW | = | 4pR*2 F |
This is the same relationship we have seen before: F = L /4pR*2, where the distance from the center of the star is replaced by the radius of the star, R*.
Intensity and the Blackbody
Spectrum
When an object is heated it can begin to glow, dull red at first, then brighter, the color changing from red to yellow to blue as the temperature rises. An ideal body that absorbs all wavelengths of electromagnetic radiation is called a blackbody. Such an ideal body has a spectrum that shows a theoretically well-defined behavior as its temperature increases:
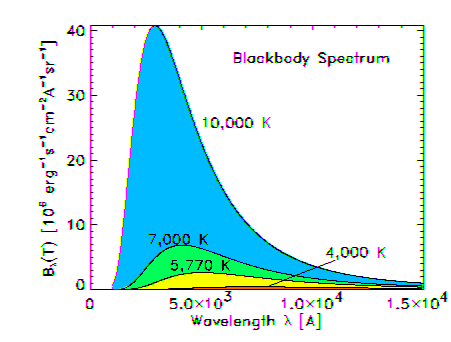
We can use the Wien displacement law to measure the temperature of stars by looking at the wavelength at which their spectrum peaks. Of course, this requires using a spectrograph, but there is an easier way. Astronomers have developed and refined a precise color filter scheme that can be used to quickly form a measure of temperature of a star. Star color magnitudes are measured through these filters (the U, B, and V filter transmission curves are shown below), and the star color index (just the difference of two color magnitudes) can be used to determine the star's color temperature. The letters stand for ultraviolet (U), blue (B) and visible (V).
In order for this scheme to work, the system has to be calibrated. The UBV system has about 100 standard stars measured in each color filter to within about 0.001 magnitude. Then if we calibrate just one of these stars in terms of energy flux through each filter, then we have the entire system calibrated. The star Vega is used as the absolute standard. The magnitudes could be (and sometimes are) written symbolically as mU, mB, and mV, but it is more common to use short-hand and write them directly as U, B, and V. Then a color index (difference of two color magnitudes) might be B-V, or U-B. Note that these are ALWAYS apparent magnitudes. If we want to talk about absolute magnitudes, we have to write MU, MB, and MV, etc.
If stars were perfect blackbodies, we could use their B-V color index to determine their temperature from the relation:
CI = B-V = -0.71
+ 7090 / T (perfect blackbody)
Note that this relation gives a color index of zero for a star of temperature 10,000 K, which is the temperature of the standard star Vega. However, stars are not perfect blackbodies. A better approximation for stars like the Sun is:
Other color filters in the infra-red have been added to the system--the R (red), I (infrared), and in the far infrared the J, H, K, L and M filters.Star Catalogs:
Star catalogs list relevant information for most of the brighter or closer known stars. The list below is a small portion of the Nearby Stars catalog, which lists all known stars within 25 pc. The star names in the first column give either the catalog numbers from other catalogs (most of the ones below are from the Gliese catalog, hence the name Gl, or just the designation NN, which means No Name. The next two columns give coordinates as they were in 1950. To find out where they are today, one would have to apply the above precession equations. Also given are the proper motion (pm), which we called m, the angle of motion, the radial velocity (vrad), the spectral type (which we will discuss below), the apparent visual magnitude (mv), several color indexes (B-V, U-B, R-I), the trigonometric parallax (ptrig), and the absolute magnitude (Mv).Quantization of Energy
Two full star catalogs are included below. We will be using these several times during the course. The standard star Vega is Gl 721.
Nearby Stars (450 kb PDF File)
Yale Bright Star Catalog (1.5 Mb PDF File)What is the temperature of the star Gl 3? Since B-V = 1.06, its surface temperature would be T = 8540 / (CI + 0.865) = 4400 K. This is near the bottom end of the allowed range for use of this equation. Clearly this is a very cool, red star.
He introduced a constant (now known as Planck's constant, h), in the energy of the waves so that each wave could only have certain allowed energies that were integral multiples of the smallest possible energy (or quantum) and obtained a functional form that agreed perfectly with all of the laws noted in the bullets above. This minimum energy E = hn, is now understood to be the energy of a photon of frequency n.
The functional form that
he derived is called the Planck function:
|
|
|||
| Bl(T) | = |
|
(wavelength form) |
| ehc/lkT - 1 |
|
|
|||
| Bn(T) | = |
|
(frequency form) |
| ehn/kT - 1 |
| inf |
|
p4 | ||
|
|
= |
|
||
| 0 | eu- 1 | 15 |
We can combine this relation
for Flux with the relation for Luminosity to get the important relation:
|
|
which relates the luminosity of a star with the temperature and radius.
With the help of the bolometric correction, which can be estimated for stars of various types, we can determine the actual luminosity of a star from its absolute visual magnitude, by comparing with the Sun.
Note that we could have written
Lo
as , Lo =4pRo2sTo4
so that R* = [0.22
(To/T*)4]0.5Ro,
to get the above answer without having to use the constants. We are
going to see this very often in this course, and thinking in this way saves
a lot of calculation. Comparing with the Table A4-3 in the text for
main-sequence K5V stars, our value of radius and temperature compare well
with the values given there. The information in Table A4-3 will come
to be used many times, and in many ways in this course.