The Big Bang--A Starting Point

The universe is expanding.  We have wonderfully precise measurements and firm evidence for this expansion:

• Increasing redshift really is correlated with increasing distance from us.
• galaxies with greater redshift are, on the whole, fainter and smaller, as we would expect for greater distance.
• gravitationally lensed sources and the "lens galaxy" causing the distortion have redshifts that agree with the extent of lensing extremely well.
• Galaxies with greater redshift really are moving away from us faster.
• supernovae in distant galaxies show the effects of time dilation due to special relativity--they explode and decay more slowly than nearby supernovae.

The expansion means that the universe was once much smaller, and running the clock backward to zero, we might imagine that the universe may have started at a single point, in the Big Bang.  If so, we can ask what things would have been like in the ultra compact, ultra high-energy environment of this point-like early universe.  We can go back to the point where our knowledge of physics breaks down, which is, indeed, incredibly far back, to much less than 1 s after the Big Bang began.

Einstein showed, with his theory of General Relativity, that we can interpret mass as a curvature in space-time.  In regions far from any mass, space-time is flat, and motions of objects proceed in straight lines in the absence of forces.  In regions near a mass, however, space-time is curved and motions proceed in curved paths (i.e. orbiting planets follow curved paths) in the absence of forces.  Thus, Einstein interprets the influence of the nearby mass not as causing a force, but as causing a curvature in space-time.   Objects (even massless photons) merely follow their geodesics or inertial paths in curves rather than straight lines.

If space-time can be curved due to the presence of mass, then the question arises as to what is the curvature of the Universe as a whole.  To understand curved space-time, let's look first at an analogy:  a one-dimensional world with a single coordinate, x, where length can be measured in only a single quantity dx.  A creature in such a world can only move in this one dimension, backwards or forwards, and would have no knowledge of any other dimensions, or directions of movement.  However, us 3-dimensional beings can view his universe from outside, and might see that his line of motion is curved into a circle, as in the figure below.

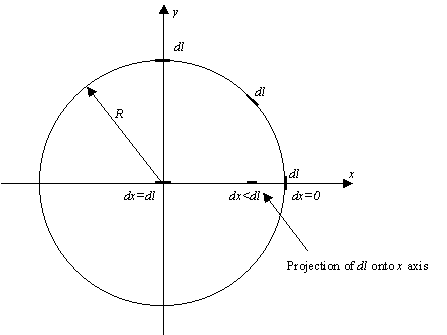
The creature would measure a distance dl along his (curved) line, and outside we would interpret his lengths as having a 1-dimensional length dx that depends on his position, because his motion is also changing its y coordinate.  We can write a metric for this space as

dl² = dx² + dy²

but since there is a relationship between the radius of curvature R and the coordinates x and y, R² = x² + y², we can write y² = R² - x².  Taking the differential, we have 2y dy = -2x dx, so that dy = -x dx/y = -xdx/(R²-x²)^1/2, to eliminate dy and write

dl² = dx² + x²dx²/(R²-x²)

which can be written

dl² = dx²/(1-x²/R²).

If we want to describe curvature in 3-dimensional space, we have the usual x, yandz coordinates, but we have to describe it in a 4-dimensional hyperspace, so we will introduce another spatial coordinate w.  Since we are 3-dimensional creatures, we cannot experience this fourth spatial dimension, but we can imagine a 4-dimensional being viewing our universe from "outside"  in order to visualize the curvature.  The curvature of our universe will again we described by a radius of curvature (or hyperradius) R.  Then we have the relationship

R² = x² + y² + z² + w².

In an obvious analogy to the 1-d case, we can eliminate w to obtain the spatial, 4-dimensional line element with a length given by

dl² = dx² + dy² + dz² + r²dr²/(R²-r²)

where we have introduced the usual expression for a 3-dimensional spherical coordinate, r² = x² + y² + z².  Note that in such a spherical coordinate system, the square of an element of length is

dl² = dr² + r²sin²qdq² + r²df²,

where we use dl for 3-d length to distinguish it from 4-d length dl.  Then we have

dl² = dr² + r² sin²qdq² + r²df² + r²dr²/(R²-r²).

We can combine the first and last terms to get

dl² = dr²/(1 -r²/R²) + r² sin²qdq² + r²df² .

Finally, we introduce scaled distances, u = r/R and du = dr/R, to find the space part of the space-time metric:

dl² = R²(t)[du²/(1 -ku²) + u²sin²qdq² + u²df²].

Here we have introduced a variable k  and allow for a radius of curvature that can change with time, to make our result more general, as we will explain in a moment.  As we said, this is the space part of the metric, and expresses the curvature of space at a single moment of time.  To include the time part, for the full expression of space-time, we simply write c²dt = c²dt - dl², or

c²dt² = c²dt²- R²(t)[du²/(1 -ku²) + u²sin²qdq² + u²df²].

You will find that this is the same expression as equation 25-6 in the text, which is called the Robertson-Walker metric.

Now we again run into trouble trying to interpret this equation for 3-dimensional space (4-dimensional space-time), because we have to step outside our universe and view it in another, hyperspatial dimension that we cannot visualize.  So let us instead consider only 2-dimensional space, with z = dz = 0, so that we can visualize the curvature as a third dimension.  We can then use the balloon analogy as follows:

• Real space is the surface of the balloon. We cannot leave the surface of the balloon.
• The radius of the balloon is R(t), which can change with time (i.e. expand as the balloon is "blown up."
• The constant k, which we said would make our result more general, represents the sense of curvature of the balloon.
• k = +1 means that the curvature is positive, like a normal balloon, and leads to a closed universe.  For a closed universe, the expansion will eventually stop, reverse, and the universe will collapse.
• k = 0 means that there is no curvature, which leads to a flat universe.  For a flat universe, the current expansion will slow and eventually coast to a stop, but not collapse.
• k = -1 means that the curvature is negative, which leads to an open universe in which the expansion will go on forever (although slowing down over time).

Let's examine the closed universe model first.  A simplified treatment is the Friedmann Model, which corresponds to conditions of uniform dust distribution of mass in the universe, with zero pressure.  In this case, we can determine the way that the curvature should change with time, which is entirely determined by the average density of the universe:

(dR/dt)² + c² = (8p/3) rGR²

It is interesting to write this in terms of the total mass of the universe, again assuming uniform dust:

M = (4p/3) R³r

so that the above equation becomes:

(dR/dt)² + c² = 2GM/R².

Consider this description of a closed universe, which will eventually stop expanding, eventually to collapse again.  In this case, dR/dt will go to zero, at which time the curvature of the universe will be the same as the Schwarzschild Radius for the universe--the universe is like one giant black hole!

It is also instructive to multiply this equation through by m/2, which gives

1/2 m (dR/dt)²-GMm/R² = -mc²/2.

The first term is the kinetic energy of the universe, the second term is the potential energy of the universe, and the term on the right is the total energy.  It is negative for a closed universe, showing that the universe does not have enough energy to expand forever.

For a flat universe, the total energy is zero, while for an open universe it is positive.  What governs whether the universe will be open, closed, or flat?  Clearly it has to do with the total mass of the universe.  If the total mass is greater than some critical mass, M_crit, then the universe will be closed.  We refer to the mass of the universe in terms of the ratio W = M / M_crit.  The closed, flat, and open universes correspond to W < 1, W = 1, andW > 1, respectively.

Going back to the balloon analogy, imagine that we are at some point on the surface of the expanding balloon.  How much of our universe can we see?  It depends only on the rate of expansion.  Imagine galaxies as dots on the surface of the balloon.  As we look at more and more distant dots (galaxies), we see them receding at higher and higher velocity.  There is some point beyond which they recede at greater than the speed of light, and so obviously we cannot see them.  So there is a limit to the size of the visible universe, but there is an "outside" that could exist but not be visible.  Note that in all of the possible universes we have mentioned, open, closed, or flat, the expansion is expected to slow down, so that recession velocities will decrease with time.  In this case, new galaxies will become visible and the size of the visible universe will increase.  What is extremely puzzling is that there is now evidence, from studies of supernovae, that the universal expansion is not slowing down, but rather is speeding up!
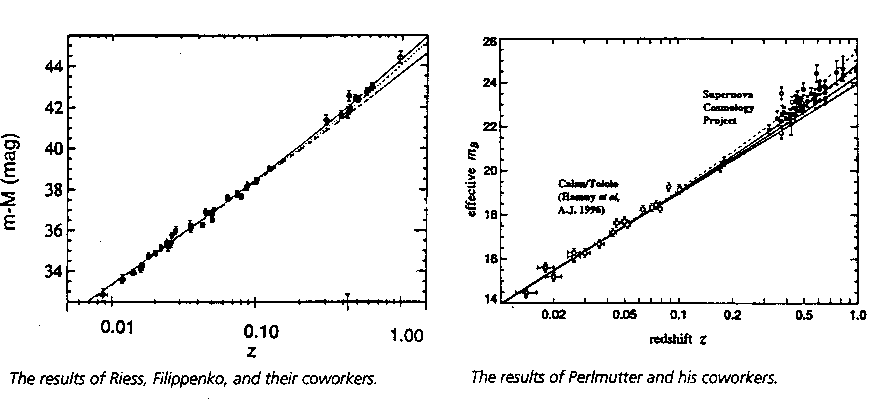
Two studies of the brightness (or distance modulus) of supernovas as a function of redshift.  If the points lie along a straight line, the universal expansion rate is constant.  However, the more distant supernovas appear to be fainter (have a higher magnitude, or a larger distance modulus) than expected from their redshifts.  This means they are moving away more slowly, and since we are seeing them as they were long ago, it implies that the universe is speeding up in its expansion.  Is the effect real, or are the data too uncertain?  The authors think it is a real effect.

If the universe did start in the Big Bang, it would have followed this scenario:

• All matter and energy begins in the form of virtual particles transforming from energy to matter and back in a seething froth.
• By 10^-6 s after the Big Bang, nucleons form.
• During the period about 100-1000 s after the Big Bang, cosmic nucleosynthesis would have formed the "primordial" mix of nuclei, mostly bare protons but about 25% by mass of Helium, and almost no heavier elements.
• The electrons in the mix would have kept the photons from escaping by interacting readily with them, allowing only a very short mean-free-path for the photons, until 10¹¹ s (~3200 y) after the Big Bang.
• At this point, the temperature of the primordial fireball drops below about 5000 K, and electrons begin to combine with the nuclei to form atoms.  The photons can now readily escape.  This is the end of the radiation era and the beginning of the matter era.
• From this point, as space continues to expand and the fireball to cool, galaxies and stars can begin to form in local condensations of matter.

All we can do is observe the present state of the universe and try to test various predictions of this scenario.  Two striking agreements are found:

• The proportion of elements that are seen in Population II (first generation) stars, star clusters, and galaxies (these elements include hydrogen, helium, and other light elements such as deuterium, ³He, and lithium) agree very well with what the Big Bang scenario predicts.
• The cosmic background (2.7 degree) radiation agrees perfectly in overall temperature and in its blackbody spectral shape.
• Also, the radiation clearly originates very far away, since predictions of how intercluster gas would affect the background as the photons pass through it agree with measurements.

However, two striking disagreements are also found:

• The universe is expanding at a rate that is far too close to that expected for the critical density (the density for which expansion goes on forever at a constant rate) that it seems highly unlikely to be chance.
• The background radiation is too uniform to explain the current "lumpiness" of the universe (the distribution of matter in galaxies, clusters, and superclusters).

An addition to the Big Bang theory, advanced to solve these problems, is the inflationary hypothesis put forth by Alan Guth, of MIT.  In this hypothesis, at a time about 10^-35 s after the start of the Big Bang, the strong nuclear force separated from the electroweak forces.  This symmetry breaking was generated by the Higgs particle.   At a critical temperature of this time, a new "phase" grew out of this symmetry breaking, forming bubbles that grew exponentially with time--much faster than the previous powerlaw expansion.  Each bubble may represent a separate universe, and our universe is one of these regions of symmetry breaking.  During the inflation period, the universe doubled in size about every 10^-35 s, until time t = 10^-32 s, during which time it expanded a size smaller than a proton to the size of a grapefruit, about 10 cm.  This expansion was much faster than the speed of light, and left its mark in the two observations above--the flatness of the universe and the lack of lumpiness of the cosmic background radiation.  As a result of inflation, areas of our universe expanded beyond our horizon (to a place we cannot reach due to the limitation of the speed of light).  If the universe were closed, the expansion would slow down and part of our universe would slow and reenter our horizon.  Such a universe has positive curvature and would eventually fall back to a Big Crunch.  However, it appears that expansion is accelerating!  This means that the universe is open, and has negative curvature.  In this case, our universe will expand forever, and part of our currently visible universe will cross beyond the rim (to use a Babylon 5 phrase).  The next generation microwave anisotropy investigations will seek to determine the cosmological parameters for our universe to much better precision than the current values.

• If the universe was created in a Big Bang, why doesn't the cosmic background radiation come from one point in the sky?
• Is space expanding or are the galaxies moving apart?
• How do astronomers know how old and how big the universe is?
• If all galaxies move away from us, doesn't that make the Milky Way the center of the universe?
• How could galaxies form if during the Big Bang everything moved away from everything else?
• If the universe is expanding, what is it expanding into?
• Is there an edge to the universe, and if so, what lies beyond?
• Did the universe expand faster than the speed of light duing the inflationary period?
• What is the fate of the universe?
• What ignited the Big Bang?