| Physics 321 |
Astrophysics II: Lecture #4
|
Prof. Dale E. Gary
NJIT
|
Atomic Structure
Atomic Structure
To understand the
origin of spectral lines, we must examine the internal structure of the
atom. In particular, we will start with a simplified model called
the Bohr model of the atom, since it
gives surprisingly good results despite its rather extreme over-simplification.
Bohr set out to explain
-
location of spectral lines of
hydrogen (Balmer series)
-
Johann Balmer measured the wavelengths
of this series of lines from atomic hydrogen and found that they fit the
relation
where RH
is the Rydberg constant RH = 10.96776
mm-1.
-
Using n = 3
gave the Ha
line wavelength, n = 4
gave Hb,
and so on.

The hydrogen line spectrum, with the pattern of Balmer lines that Bohr
set out to explain.
In the Bohr model, the nucleus
is considered to be a point mass located at the center of the atom, while
the electrons move in circular orbits around it, something like
the solar system with planets moving around the Sun.
The positive charge of the
nucleus and the negative charge of an electron give the electrostatic attraction
force required to keep the electron in uniform circular motion. Bohr's
Postulates:
-
Only a discrete number of orbits is allowed to the electron
(only those with angular momentum that is an integral multiple of h/2p)
and when in these orbits the electron cannot radiate.
-
Radiation of a discrete quantum of energy is emitted or
absorbed only when the electron jumps from one orbit to another, and the
energy of the radiation equals the energy difference between the orbits.
Derivation of Quantized Energy
levels
The circular orbits postulated
for the electrons around the nucleus of the atom means that there must
be a central force (centripetal force) mv2/r
provided by the attraction between the negatively charged electron and
the positively charged nucleus. This attraction is the electric force
between two charges (the Coulomb interaction), whose magnitude is
F = (4peo)-1q1q2/r2
=
(kZe)e/r2=mv2/r
(1)
where for convenience we use
k
= (4peo)-1=
8.99 x 109 N m2/C2.
Recall that the angular momentum is mvr,
and so Bohr's postulate about angular momentum is equivalent to:
Combining equation (1) with
(2), we can solve for r, the
radius of the orbit, as
r = aon2
= n2(h2/4p2me2kZ).
(3)
where
ao=
5.29 x 10-11
m is the Bohr
radius for the ground state of the hydrogen atom.
Looking at the meaning of
this equation, it says that electrons are allowed only orbits of certain
(quantized) radii, where n =
1, 2, 3... We will look at this further in a moment.
Associated with these quantized
orbits is a quantized energy. Total energy is the sum of kinetic
energy and potential energy, E = K + U.
We are free to choose the zero of potential energy any way we wish, since
only differences in potential energy are important. We will take
the zero of potential energy at infinity. The potential energy
difference is just the negative of work, or force times the displacement,
so the potential energy of an electron inside an atom is
|
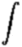 |
r |
kZe2 dr
|
|
| U = |
|
|
= - kZe2/r |
|
inf |
r2
|
|
so that the total energy is
and using equations (1), (2)
and (3) above, after some manipulation we find the quantized energy
E(n) = -(2p2me4k2Z2)/n2h2.
Note that the total energy is
negative,
which means that the electron is bound, and that as n ->
infinity, E ->0.
The number n is called the principal
quantum number.
The quantity (2p2me4k2Z2)/h2
is a constant that depends only on fundamental physical quantities,
R' = (2p2me4k2)/h2
= 13.6 eV.
The electron-volt (eV) is a
unit of energy (the energy an electron would gain after acceleration through
a potential of 1 volt). 1 eV = 1.602 x 10-19
J. Using the symbol R'
for this constant, the total energy equation becomes extremely simple:
Wave Particle Duality and Uncertainty
Principle
Photons are "light particles,"
but light, of course, also has wave characteristics. These two different
views, wave vs. particle, are related in the expressions for photon energy
(E = hn)
and photon momentum (p = h/l).
de Broglie postulated that these photon relationships also hold for massive
particles, and that a frequency and wavelength could be derived from:
where E
and p are the classical energy
and momentum of the massive particles. This has been verified by
many experiments, and is called wave-particle duality. Related to
this is the Heisenberg Uncertainty Principle, which has two forms:
-
Dx
Dp
~ h/2p
-
DE
Dt
~ h/2p
Spectra from the Hydrogen Atom
The Bohr model of
the hydrogen atom (Z = 1) gave
us the following results:
The angular
momentum, l, was postulated
to be quantized according to
l = mvr = nh/2p.
where n is the principle quantum
number.
The radii
of allowed electron orbits were also quantized according
r = aon2
= n2h2/(4p2ke2m)
where
ao=
5.29 x 10-11m
is the Bohr
radius.
The energies of the orbits were
likewise quantized according to
where R' = 13.6
eV
is a constant.
The difference between energy
levels (orbits) corresponds to a wavelength
1/lab
= nab/c
= (Eb -
Ea)/ch=RH[1/nb2-1/na2]
where RH=
10.96776
mm-1
is the same Rydberg constant that was
measured experimentally by Rydberg.
One way to see why the angular
momentum should be quantized is to consider the electron as a wave.
As de Broglie showed, particles exhibit wave characteristics with wavelength
given by
l
= h/p = h/mv
What if the lowest orbit corresponded
to one wavelength of such an electron wave? The circumference of
the orbit would correspond to a wavelength, so
2pr
= l = h/mv
=> l = mvr = h/2p.
The next
higher orbit would correspond to two electron wavelengths, and the nth
orbit to n
electron wavelengths, so in this way we naturally find l
= nh/2p.
If the orbit corresponded to a non-integer multiple of the electron wavelength,
the electron wave would overlap and interfere with itself.
Here
is a scale model of the orbits of the hydrogen atom, with the radii getting
further apart according to n2:
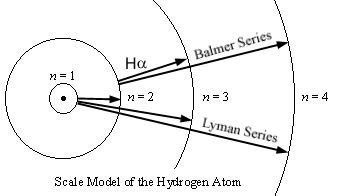
However, despite the orbits
getting ever farther apart in space, they get closer together in energy
according to 1/n2.
Any energy level diagram is shown below:
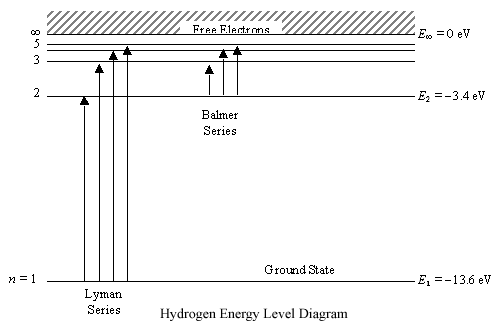
Heisenberg Uncertainty Principle
We noted earlier
the relationships:
Dx Dp
~ h/2p
DE D
t
~ h/2p
Let us now show some effects
that come from them. The n = 2 level of hydrogen lives for
a very short time, only about 10-8 s.
That is, an electron in the first excited state will, after about 10-8
s, spontaneously emit a photon of energy 10.2 eV and go back to the ground
state (emitting a Lyman a
photon). The second relation, above, means that the photons emitted
have an energy uncertainty of
DE ~ h/2pD
t
=
1.05 x 10-19 erg => Dl
~ l2/2pD
t
c = 0.014 mA
This uncertainty in the wavelength
shows up as a broadening of the spectral line (natural broadening).
Similarly, we can ask what
is the uncertainty in speed that is required of an electron that is confined
in a hydrogen atom (in the ground state orbit, with Bohr radius ao=
5.29 x 10-11
m).
Example: Imagine
an electron comfined within a region of space the size of a hydrogen atom.
What is the minimum speed and energy of the electron, estimated using the
Heisenberg uncertainty principle? We know Dx
~ ao=
5.29 x 10-11mso
Dp ~ h/2pao
= 6.62 x 10-34
J s/2p(5.29 x 10-11m)
= 1.99 x 10-24 kg
m/s.
This is
the uncertainty in the momentum, which is about equal to the minimum momentum
pmin
that the electron has in order to be confined within the atom. Now
the momentum is just p = mv,
so the momentum, so the minimum velocity is
vmin
= pmin/me
= 1.99 x 10-24
kg m/s / 9.1 x 10-31
kg = 2.19 x 106
m/s.
The corresponding minimum kinetic
energy is
Kmin
= 1/2mev2min=
2.18 x 10-18
J
which may seem like a small
energy, but when converted to electron volts, this is
Kmin
= 2.18 x 10-18
/ 1.602 x 10-19
J/eV = 13.6 eV!
This is exactly the energy of
an electron in the ground state of the hydrogen atom! Later we will
see that this subtle quantum effect is responsible for supporting the tremendous
gravitational weight inside a white dwarf star.


