Hertzsprung-Russell Diagram

We now discuss one of the most important diagrams in Astronomy, a way of organizing and presenting information about all of the various kinds of stars, with which we can instill order from the cosmos and understand the internal workings of the stars even though we see most of them as a mere point of light.  You have all taken some simple measurements of nearby stars -- the B-V color index and the absolute magnitude (which required measurements of apparent magnitude and trigonometric parallax) -- and made for yourself a Hertzsprung-Russell or H-R diagram.  The same diagram can be presented in different, but equivalent ways:
• M_VvsB-V (the kind you made, called a color-magnitude diagram)
• M_V  vs  Spectral Type
• Luminosity vs Temperature (L-T diagram -- a theorist's diagram)


The first thing we note is that the stars tend to fall in a fairly narrow band, stretching diagonally across the diagram.  This band is called the main sequence, because most stars (between 80 and 90% of all stars) lie along it.


Figure 6.1 H-R Diagram of Stars Within 25 pc of the Sun

Clearly the bluer stars (zero or negative B-V) tend to have higher absolute magnitudes, while red stars (large positive B-V) have lower absolute magnitudes.  Remember that we can convert absolute magnitude to luminosity, through the equation

M_sun -M_* = 2.5 log L_*/L_sun
where the magnitudes are bolometric magnitudes, after applying the bolometric correction.  Likewise, we can convert color index to temperature (approximately) according to
CI = B - V = -0.865 + 8540 / T   (4000 K < T < 10000 K)
and similar conversions can be made for other temperature ranges.  In this way, we can change from the color-magnitude diagram based on observation to the luminosity vs temperature diagram based on physics.

We can ask what causes the relationship we see between luminosity and temperature.  We know that these two are related by

L = 4pR_*²F= 4pR_*²sT ⁴
where R_* is the radius of the star, and s is the Stefan-Boltzmann constant.  If all stars are the same size, the H-R diagram would show just such a variation, with blue stars appearing brighter than red stars just due to the T ⁴ increase in blackbody flux output.  However, the main sequence is much steeper than this, and cuts across lines of equal stellar radii, as you can see in the figure below.  The stars must actually get larger as they get bluer, or more correctly, they must get bluer as they get larger.  This is a powerful clue as to how stars work.
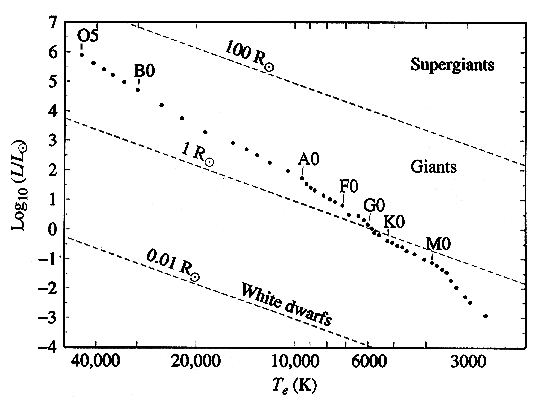
Figure 6.2 HR diagram with lines of constant stellar radius superimposed.

In addition to the stars that lie on the main sequence, Figure 6.1 shows a few stars off the main sequence, both above and below.  The ones below must have a smaller size than ones on the main sequence at the same color index.  The ones above must have a larger size.  Note that the ones above tend to be red (cool), while the ones below tend to be blue-white (hot).  These are, not surprisingly, called red giants and white dwarfs, respectively.  Note that once we plot a star on an L-T diagram, we know its radius.  We find

• Main sequence stars range in size from 0.08 R_sun at the cool, red end (M stars) to about 60 R_sun at the hot, blue end (O stars).
• White dwarfs are at 0.01 R_sun or smaller.
• Red supergiants can reach 300 R_sun or even larger.

We have used the terms giant, supergiant, dwarf, without defining them.  Because of the relationship between size and luminosity, the size categories correspond to luminosity class.  The Morgan-Keenan (M-K) system is based on spectra.  One can see subtle differences in spectra of stars of otherwise similar spectral type, due to the different sizes of the stars.  One of the main effects is the width of the spectral lines, which get narrower for more luminous stars, as may be seen below:

Figure 6.3 Spectra near spectral type F5, for different luminosity classes
Adapted from data in the electronic version of "A Library of Stellar Spectra,"
by Jacoby G.H., Hunter D.A., Christian C.A.  Astrophys. J. Suppl. Ser., 56, 257 (1984).

The M-K system of luminosity classes are shown in the table below, and their position on the H-R diagram is shown in Figure 6.4, below.

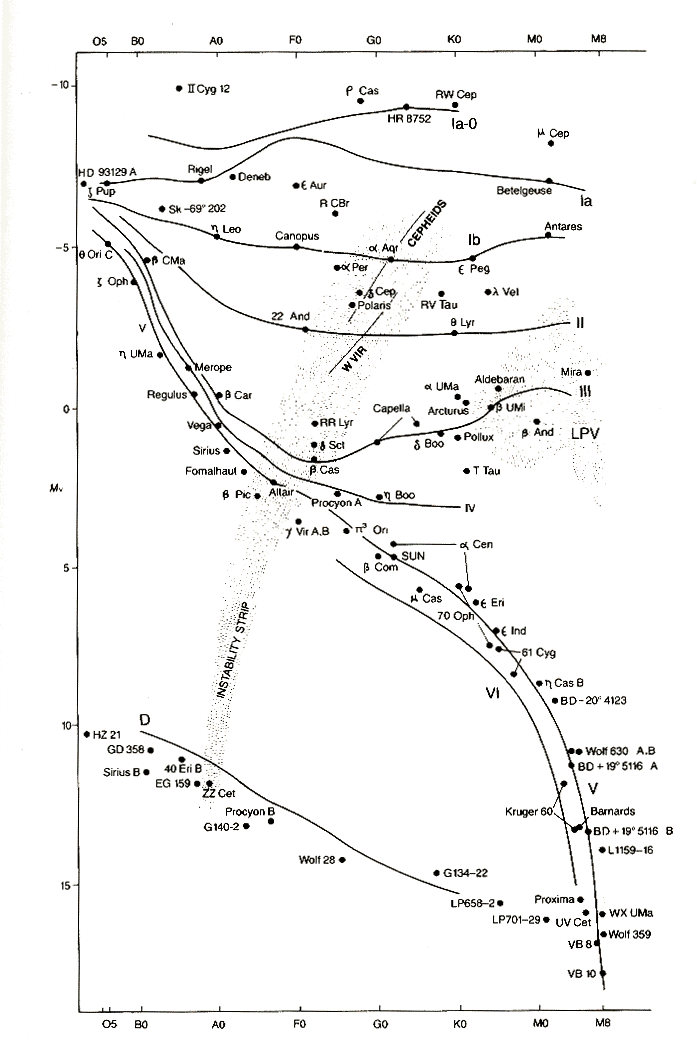
Figure 6.4 An H-R diagram showing the Morgan-Keenan luminosity classes,
along with locations in the diagram for some nearby or bright stars.
 

Class	Type of Star
Ia-O	Extreme, luminous supergiants
Ia	Luminous supergiants
Ib	Less luminous supergiants
II	Bright giants
III	Normal giants
IV	Subgiants
V	Main-sequence (dwarf) stars
VI	Subdwarfs
D	White dwarfs

The M-K classification scheme enables astronomers to place a star on the H-R diagram solely on the basis of the star's spectrum.  Once the star is placed on the H-R diagram, one can simply read off the absolute magnitude M_V from the vertical scale, and from its measured apparent magnitude find its distance from

m_V - M_V = 5 - 5 log d

Such a distance determination is called spectroscopic parallax, although note that it has nothing to do with parallax.  It is simply a distance determination based on its spectral type.  Note that because the luminosity classes are of finite extent in magnitude, this method is only good to roughly +/- 1 magnitude, which corresponds to a distance accuracy of about 10^1/5 = 1.6.

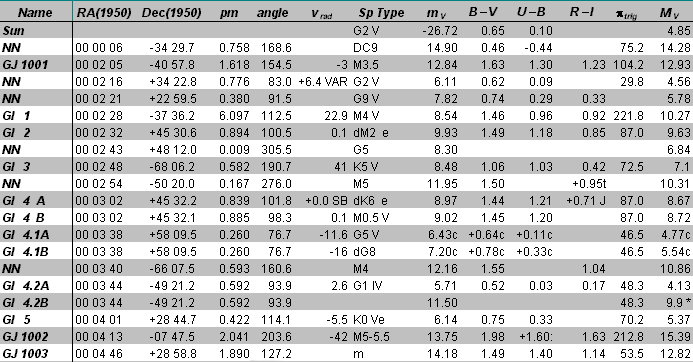
Let's compare spectral types from our catalog with the listed absolute magnitudes.  Star Gl 3 is listed as a K5 V (a K5 main-sequence, or dwarf star), and looking up that spectral type in Table A4.3 of the text, we find a predicted absolute magnitude of 8.0.  The absolute magnitude listed above is 7.1 -- somewhat brighter than predicted.  The star GJ 1003 has a listed spectral type of 'm', which must mean that the spectral type is uncertain, but it is some type of M star.  If we assume that it is luminosity class V, then from its measured absolute magnitude of 12.82 we would predict that it should be somewhere between M5 and M6.  Its B-V color index, however, would place it as about M2 or M3.  You can see that Table A4.3 is not exactly precise, but it makes a useful guide.

Now let us focus on individual spectral line shapes and see what more they can tell us about the physical conditions in stars.  One simple measurement we can do is the width of the spectral line, but spectral lines can have different shapes.  A precise definition of line width that is independent of line shape is given by the equivalent width, which is defined as
 

				Fc - Fl
W	=				dl
				Fc

where F_c is the flux of the continuum, and F_l is the flux elsewhere in the line.  The figure below shows the relationship between the equivalent width and the shape of the line, for a normalized line profile.

Normalized line profile and equivalent width.  Note that the blue-shaded region above the line has the same area as the blue-shaded region below the line, so the equivalent width has the same area as the line itself.

The width of the line is contributed to by three main effects:

• Natural Broadening
This is the effect we already discussed, relating the lifetime of an energy state Dt with the uncertainty in energy DE due to the Heisenberg Uncertainty Principle.  This uncertainty in energy corresponds to an uncertainty in wavelength:
 

	l2	(	1		1	)
Dl =				+
	2pc		Dti		Dtf

The natural broadening of the H-alpha line is about 0.46 mA (very small).
 

• Doppler Broadening
This is due to the thermal and/or turbulent motion of atoms in the atmosphere of the star.  A moving atom absorbs a photon that is slightly shifted in wavelength due to the doppler shift Dl/l = +/- | v_r |/c.  If the velocity is due to thermal motion, v = [2kT/m]^1/2, then we have a width of
 

	2l	(	2kT			)	1/2
Dl =
	c		m

where the factor of 2 is due to the motion both toward and away from the observer.  Turbulent motion with a velocity v_turb can be included as
 

	2l	(	2kT			)	1/2
Dl =				+	v2turb
	c		m

Doppler, or thermal, broadening of the H-alpha line for the Sun (T = 5780 K) is about 0.43 A, or 1000 times greater than natural broadening.
 

• Pressure Broadening
When the stellar atmosphere is very dense (large number n of atoms per cubic meter), an additional source of broadening comes into play.  An estimate for the effect of pressure broadening can be obtained by taking the equation above for natural broadening, and replacing the lifetime Dt with the mean time between collisions among atoms.  This time is Dt = l/v where l = ns is the mean-free-path and s is the collision cross-section.  The collision cross-section is just the "area" of the atom, and these values are tabulated for different species.  Here, of course, we will again use the thermal speed v = [2kT/m]^1/2.  Putting it all together, we have
 

	l2 ns	(	2kT			)	1/2
Dl =
	pc		m

Note that this broadening is proportional to the density of atoms.  This explains the narrowing line profiles as we go up in the Morgan-Keenan classification to more luminous stars.  The supergiant stars have such large sizes that their outer atmosphere is very low density.  The pressure broadening term is absent in such stars.  Dwarf stars, on the other hand, have appreciable broadening (in the Sun, the H-alpha line is broadened by 0.24 mA, for example).

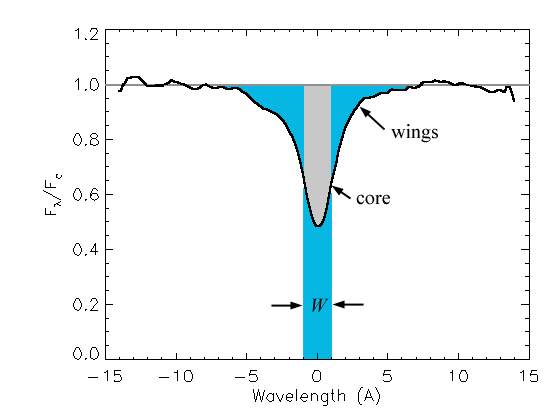
The total line shape is the sum of these three effects (plus some other effects such as stellar rotation or pulsations, which do not have simple expressions).  The total line profile is called a Voigt profile.  Doppler widths contribute mostly to the line core (see the figure above) while pressure effects contribute more to the line wings.

In addition, the line profile changes depending on the number of atoms per unit area, (column density) N_a contributing to it.  For the H-alpha line, this would be the number of H I atoms along the line of sight that are in the n = 2 state.  Here is the behavior as the column density N_a grows:

• The line grows deeper, and the equivalent width grows linearly with N_a.
• Ultimately the core of the line saturates.  At this point the wings continue to grow deeper and broader, but the core gets flatter.  The equivalent width now grows much more slowly, as (lnN_a)^1/2.
• As the wings grow deeper, the pressure-broadening grows more important and the equivalent width grows more quickly again, but still not as quickly as at first, going as N_a^1/2.


It is possible to draw a curve of growth that expresses how the equivalent width log W/l changes with log f N_a(l/5000).  This is shown for the Sun in the figure below.  Here, f is the oscillator strength for the transition, and is a value tabulated for each electron transition in an atom that expresses the relative likelihood of that transition occurring rather than another from the same initial energy level.


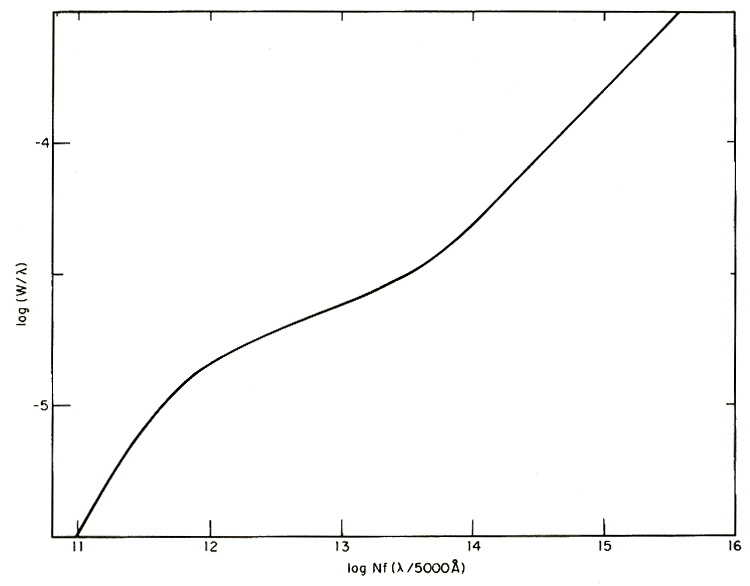
A general curve of growth for the Sun, where N is in atoms/cm². (Figure from Aller, Atoms, Stars, and Nebulae,
Revised Edition, Harvard University Press, Cambridge, MA, 1971).

Example:
We will use the above curve of growth to find the number of sodium atoms above each square centimeter of the Sun's surface from measurements of two sodium lines given in the first two columns of the table below.  The third column is the oscillator strength f measured in the laboratory, and the last two columns are just combinations of the first three columns, for calculation convenience below.
 

l (A)	W (A)	f	log (W/l)	log[f (l/5000 A)]
3302.38	0.088	0.0214	-4.58	-1.85
5889.97	0.730	0.645	-3.90	-0.12

Values of the Sun's surface temperature T = 5800 K and pressure P = 0.01 N/m² were used to construct the above curve of growth, and will be used in this example.

Both of the lines are produced when an electron makes an upward transition from the ground state of the neutral sodium atom (Na I) and so they both have the same value of N_a, the number of absorbing sodium atoms per unit area above the surface.  This number can be read from the figure, using the values in the table, to obtain the value of log[f N_a(l/5000 A)] for each line.  The results are:
 

log[f N_a(l/5000 A)] = 13.20        for the 3302.38 A line
                             = 14.83        for the 5889.97 A line


To obtain the value of the number of absorbing atoms per unit area, N_a, we use the measured equivalent widths, in the form of the last column of the table, log[f (l/5000 A)], together with

 
log N_a = log[f N_a(l/5000 A)] - log[f (l/5000 A)]
            = 13.20 - (-1.85) = 15.05        for the 3302.38 A line
            = 14.83 - (-0.12) = 14.95        for the 5889.97 A line.


The average value of log N_a is thus 15.0, so there are about 10¹⁵ Na I atoms in the ground state per cm² area of the Sun's surface.

To find the total number of sodium atoms, we use the Boltzmann and Saha equations from the previous lecture.  The difference in energy between the final and the initial states, E_b -E_a, is just the energy of the emitted photon, so in the Boltzmann equation
 

exp[-(E_b -E_a)/kT] = exp[-hc/lkT] = 5.45 x 10^-4        for the 3302.38 A line
                                                    = 1.48 x 10^-2        for the 5889.97 A line.
and so nearly all of the neutral Na I atoms are in the ground state.  All that remains is to determine the number of sodium atoms per unit area in all stages of ionization.  If there are N_I = 10¹⁵ neutral atoms, then the number of singly ionized atoms, N_II, comes from the Saha equation:
 
 

NII		2kTZII	(	2pmekT	)
	=					exp(- cI/ kT )
NI		PeZI		h2


Using atomic parameters for Na, Z_I = 2.4, Z_II= 1.0 (partition functions), and c_I= 5.14 eV for the ionization potential, the above equation evaluates to N_II/N_I= 2.43 x 10³.  This means that there are about 2430 singly-ionized sodium atoms for every neutral atom, so N_II = 2.43 x 10³ N_I = 2.43 x 10¹⁸ cm^-2.

Where to find atomic data (ionization potentials, oscillator strengths)