Clusters and Main Sequence Fitting

We mentioned earlier the idea of finding distances to stars using spectroscopic parallax.  There is a related method for finding the distance to star clusters, which is an extremely important thing to know.  Why are clusters important?  We can be relatively sure of three things about star clusters, such as the one below:
1. All of the stars are at nearly the same distance.
2. All of the stars were born at nearly the same time.
3. All of the stars have the same composition, since they were born from a single cloud (as we will discuss later).



A Globular Cluster, M3

If we look at the H-R diagram of a star cluster, such as the one below, we see that it is quite different from the one we made from the nearby stars catalog.  This difference is a very important clue about the way stars evolve.


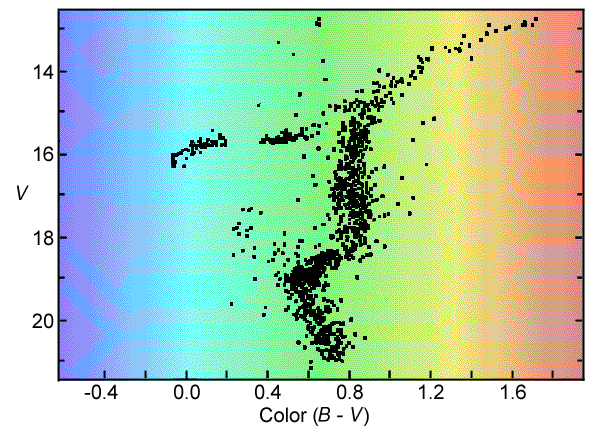
The H-R (color-magnitude) diagram for the globular cluster M3.

We can use the cluster H-R diagram above to find the distance to the cluster by comparing it with a calibrated H-R Diagram such as the one we constructed earlier from the Nearby Stars catalog.  Such a comparison uses the technique of main sequence fitting as illustrated below.  Here we have scaled the cluster diagram (shown in red) to the same scale as the calibrated H-R diagram, and shifted it keeping the B-V values aligned, until the main sequences overlap.  We can then read the distance modulus directly off the graph.  In this case it is about 15.4, which places the cluster at about 12 kpc.


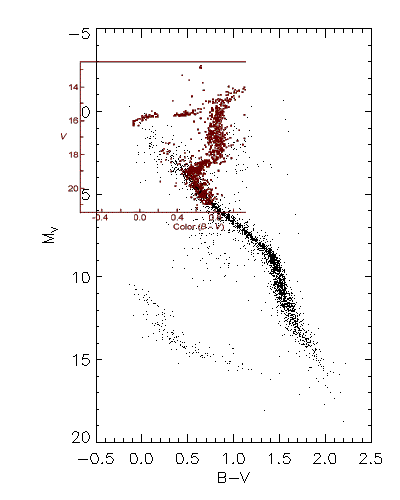
Main Sequence Fitting--comparison of the H-R diagram
of M3 with the calibrated H-R diagram of nearby stars.

We will come back to the use of cluster H-R diagrams for another purpose, the determination of the age of the universe!  But first we have to learn something about stellar evolution.

To understand why stars differ from one another in different parts of the H-R diagram, we have to look at their basic properties.  Every star is a giant sphere of hot gas (actually a plasma), and certainly those along the main sequence are pretty much made of the same stuff.  The main essential properties that cause them to differ are pressure P, temperature T, and composition, characterized by the mean molecular weight, m.  Let's look at composition, first.

Stars are made of relatively simple stuff.  By mass, our Sun is 73% hydrogen, 26% helium, and only 1% of higher Z (atomic number) atoms.  We write these quantities in terms of the mass fraction, as

• X = m_Hn_H / r = density of hydrogen / total density
• Y = m_Hen_He / r = density of helium / total density
• Z = m_Zn_Z / r = density of everything else / total density

The way that composition plays a role in stellar structure is mainly through the mean molecular weight, defined in terms of its inverse as:
 
1/m = m_Hn/ r                               (1)


where n is the number density (particles cm^-3) of particles of all types, i.e. n = n_e + n_H + n_He + n_Z.  This is the number density of electrons plus all of the kinds of atoms.  A good approximation for most star interiors is that the gas is fully ionized.  For a fully ionized gas, how many electrons will there be?  Each hydrogen atom will contribute 1 electron.  Each helium atom will contribute 2, and each higher element will contribute Z (that is, a number equal to the atomic number of the element).  In this case, we have the mean molecular weight given by:
 

1/m = 2 X + 3/4 Y + 1/2 Z


For the Sun, X = 0.73, Y = 0.26, and Z = 0.01, so 1/m ~ 1.67.  The other atoms besides hydrogen and helium are referred to in astronomy as metals, and the value of Z is called the metallicity.

Pressure is force/unit area, F / A.  The atmospheric pressure at sea level is about 14 lbs/square-inch, or 10 Pascal, or 1000 millibars (mm of mercury).  Pressure in the interior of a star arises from the weight of the atmosphere directly above the point--that is, from the force of gravity--balanced by the outward pressure due to energy release inside the star.  Nearly all stars are static, meaning that they are not expanding or contracting significantly.  Such a state is called hydrostatic equilibrium, and like all equilibrium situations, it is characterized by force balance.  Consider a column of gas of cross-sectional area A.  The forces on a section (parcel) of the gas is shown in the figure on the left:

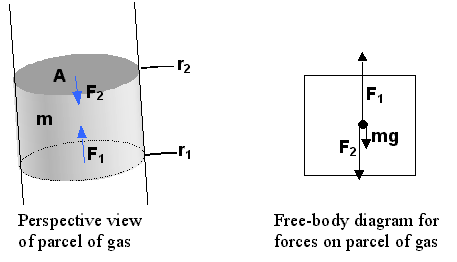
The mass of the parcel is related to the mass density by r = m / V = m / A(r₂ - r₁).  From the free-body diagram it is clear that
 
F₁ = F₂ + mg = F₂ + A(r₂ - r₁) rg
which can be rearranged to
 
DF / A = DP = - Drrg


where DP is the pressure difference (P₁ - P₂) on the two ends of the column section, and Dr is the radius difference (r₁ - r₂).  Taking the limit as Dr approaches zero, we obtain the equation of hydrostatic equilibrium:
 

dP/dr = -rg                        (2)


There is another relationship we can obtain between pressure and density (and temperature) called the equation of state.

The temperature, density, and pressure are not independent, but are joined by the equation of state, which describes the macroscopic manifestation of particle interactions.  One well-known example of an equation of state is the ideal gas law:

PV = NkT

where P = pressure, V = volume, N = number of particles, k = Boltzmann's constant, and T = temperature.  We can write this more simply in terms of the number density n = N / V as

P = nkT.

Above in equation (1), we saw that the number density is related to the mass density by

n = r/mm_H

so the equation of state becomes

P = rkT / mm_H .                       (3)

Inserting (3) into (2), and assuming for the moment that temperature T does not change with height (an isothermal atmosphere), we obtain an expression for the density:

dr/dr = - (mm_Hg / kT) r            (4a)

which is a first-order differential equation with the solution:

r = r_o exp(-r / H)

where H = kT / mm_Hg  is called the scale height. and r_o is called the base density since it is the value of the density at r = 0.  Note that if we had solved for r in equation (3) and substituted it for r on the right-hand side of equation (2), we would obtain a similar differential equation for the pressure:

dP/dr = - (mm_Hg / kT) P            (4b)

with the solution:

P = P_o exp(-r / H).

Therefore, the pressure and density vary with the same scale height.  What is the physical interpretation of the scale height?  It means that the pressure and density drops with height by the same factor of 1/e = 0.368 for each increase in height of a distance H.  Note that a hot atmosphere (large T) has a larger scale height than a cool atmosphere.  Also, increasing gravity lowers the scale height.  It is of interest to calculate the scale height for some atmospheres.

Example 1: Scale height at Earth's surface.  H = kT / mm_Hg, where T ~ 300 K, g = 9.8 m/s², but what is m?  The atmosphere is mostly (4/5) molecular nitrogen, N₂, which has a mean molecular weight of 28.  Using these values, we obtain:

H = kT / mm_Hg = (1.38x10^-23 J/K)(300 K) / [28(1.67x10^-27 kg)(9.8 m/s²)]
    = 9.0 km

In fact, the Earth's atmosphere rapidly grows cooler with height, so the scale height is somewhat smaller.

Example 2: Scale height in the photosphere of the Sun.  Here, T = 5770 K, m ~ 0.6, but what is g?  Remember that mg is the force of gravity, which is also

F  = mg = GMm / R²

so g = GM / R².  At the surface of the Sun, we would use M = 1.989x10³⁰ kg, R = 6.96x10⁸ m (from Appendix 7 in the text), so

g = (6.67x10^-11 N m² / kg²)(1.989x10³⁰ kg)/(6.96x10⁸ m)² = 296 m/s². ~ 30 g

Then,

H = kT / mm_Hg = (1.38x10^-23 J/K)(5770 K) / [0.6(1.67x10^-27 kg)(296 m/s²)]
    = 270 km

In the atmospheres of stars and planets, the ideal gas law is a pretty good approximation.  However, in the interiors of stars some new effects can come into play.  In any star, near the core, especially, the light itself can exert significant pressure.  A photon has momentum p = hn/ c, and when it is absorbed or reflected it exerts a force F = dp/dt.  Consequently, electromagnetic radiation has an associated pressure.  It may come as no surprise that the pressure is related to the total radiant energy flux, which we saw from the Stefan-Boltzmann law was F = sT⁴.  One can show that

P_rad = 1/3 aT ⁴

where a = 4s/c = 7.56591 x 10^-16 J m^-3 K^-4 is the radiation constant.  In this case, the total pressure, equation (3), is replaced by

P = rkT/ mm_H + 1/3 aT ⁴                      (3')

Finally, when relativistic and quantum effects are included to derive the equation of state, a very different pressure equation is found that applies to extremely dense states of matter such as found in white dwarfs and neutron stars.  We will look into this later in the course.