Stellar Energy Sources

It is now time to ask what it is that powers stars, to produce the tremendous luminosity (energy/s) that causes them to shine so brightly.  The solar luminosity is L = dE/dt = 3.826 x 10²⁶ J/s.  We can estimate the total energy E available from various processes, and then calculate the lifetime of the Sun if it shines at its current rate:
 
Dt = DE / L.

In the mid 1800's, during the industrial revolution, it was natural to consider that the Sun was perhaps some sort of burning fuel, such as coal.  Burning, of course, is a chemical process (oxidation) that releases energy by rearrangement of chemical bonds--that is, it involves bound electrons.  If every atom in the Sun were available to release an energy of, say, 10 eV, how much energy would that be?  Since the Sun is mostly hydrogen, the number of hydrogen atoms would be n = M_sun/m_H = 1.989x10³⁰/1.67x10^-27 ~ 10⁵⁷ atoms.  Since each provides 10 eV = 1.6x10^-18 J, the total energy available would be 1.6x10³⁹ J.  Then the lifetime would be

Dt = DE / L = 1.6x10³⁹/3.8x10²⁶ ~ 5 x 10¹² s ~ 170,000 years.


Of course, coal is much less efficient than the extremes that we assumed, and the answer was only about 2000 years in that case.
 

Another possibility is that stars shine simply due to the release of gravitational potential energy.  If the Sun were once much larger than it is now, perhaps it simply grew smaller, slowly collapsing in on itself.  Again we can estimate the amount of energy available from such a collapse, and see how long the Sun could shine if gravitational potential energy were the only source of energy.  Gravitational potential energy is given by
 
U = - GMm / r                (1)


and is negative because we define the zero of potential energy at infinity.  Starting with an initial configuration, or arrangement of mass, as we move mass toward the center of gravity of the arrangement the potential energy decreases (becomes more negative) indicating that the kinetic energy must have increased.  Considering now the case of a spherical distribution inside a star, we can add up all of the contributions to potential energy by integrating over the mass of the star:
 

dU = - GM_r dm / r          (2)


where dm is the element of mass at radius r from the center of the star, and M_r is the interior mass--that is, the mass contained within the sphere of radius r interior to the point in question.  We have made use of two facts in going from (1) to (2):
 

• The gravitational potential outside of a sphere (or spherical shell) is the same as it would be if all of the mass were concentrated at a point at its center.
• The gravitational potential inside of a spherical shell is zero.


Both of these can be proved using simple calculus, and were first shown by Isaac Newton.  This applies only to spherical shells of uniform density, which happily is a condition well met by stars and many other objects.  Note that each shell can have a different density from all of the others, rather like an onion.

Given this onion-like structure, we can consider the shell of uniform density r, at radius r and thickness dr.  Such a shell will have a mass dm = 4pr²r dr.  Inserting this into (2), we have

dU = - GM_r4pr²r dr / r

which can be integrated over the radius of the star, from the center (r = 0) to the surface (r = R) to give the total potential energy of the star:

 

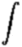		R
U = - 4pG			Mr rrdr         (3)
		0

In this expression, note that M_r is itself an integral, since the total mass interior to the radius r requires integrating the density from the center to the point r:

 

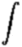		r
Mr = 4p			rr2dr         (4)
		0

so the entire expression requires the change of density with radius in the star.  However, we can make some simplifying assumptions to see if gravitational potential energy can be the energy source for the Sun.  Let's assume that the density is constant, with the value of the average density <r> = M_r / (4/3 pR³), so that (4) becomes M_r ~ 4/3 pr³<r>.  Then the potential energy, (3), becomes
 

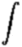		R
U ~ - 4pG <r>2			4/3 pr4dr
		0

or
 

	16p2				3GM 2
U ~ -		G <r>2R5	~	-
	15				5R

We will discuss in a moment the virial theorem, which says that a gravitational system moving from one equilibrium state to another will release 1/2 its available energy as internal kinetic energy, and the other 1/2 is available to be radiated away.  Thus, if in the initial configuration all of the mass is at infinity (zero potential energy) then the amount that can be radiated in getting to the final (current) configuration is -U/2, or

DE = E_f-E_i = -U/2 = 3GM² / 10R

In the case of the Sun, this is DE =3GM² / 10R ~ 1.1 x 10⁴¹ J.  Again, since the Sun shines at the rate L = dE/dt = 3.826 x 10²⁶ J/s, it will take only

Dt = t_KH = DE / L = 1.1 x 10⁴¹ J / 3.826 x 10²⁶ J/s ~ 10⁷ years.

This time, t_KH is called the Kelvin-Helmholtz time scale, and was calculated near the turn of the century.  At the time, this was considered an iron-clad argument that the Earth and Sun coud not be much older than this, although geologists and paleontologists were finding that the Earth must be much older.  We now know from radio-active dating techniques that the Earth and Moon are at least 4.5 billion years old.  Clearly there must be another source of energy for the Sun.  We have looked at gravitational energy in some detail, however, because for some objects and at some parts of their life-cycle gravitational energy is the dominant energy source.

As we mentioned, the virial theorem states that when a system is in one equilibrium state and changes to another equilibrium state, the difference in energy goes equally into two parts: (1) the internal energy of the system and (2) radiation or other loss mechanisms.  What do we mean by equilibrium?  An equilibrium is a situation in which the configuration of the system is not changing.  However, by the phrase "not changing" we do not mean that the system cannot evolve.  Rather, the system is allowed to change only slowly over some relevant timescale.  Consider a planet orbiting around a star.  If the planet orbit does not change appreciably over many orbits, then the system can be said to be in equilibrium.  Consider a collapsing cloud of gas.  If many collisions between particles occur before the cloud changes radius appreciably, the system can again be said to be in equilibrium.

In the collapsing cloud example, above, we used the virial theorem to find the amount of energy radiated away.  The virial theorem also says that this same amount of energy (3GM² / 10R) goes into internal energy (kinetic energy, or heat in this case).  It the cloud starts out at temperature 0 K, what will be its temperature at radius R?  The number of particles in the cloud is N = M / mm_H.  and each has thermal energy is 3/2 kT, so the total thermal energy is

3/2 NkT = 3GM² / 10R

so the temperature change is

DT = T_f - T_i = GM ² / 5RNk = GM mm_H / 5kR ~ 2.78 x 10⁶ K

where the numerical value is found using solar values for the mass and radius.  In fact, the internal temperature of the Sun is higher than this, as we can see by simple application of hydrostatic equilibrium and the ideal gas law:

• Average density of Sun: <r> = M_sun/4/3pR²_sun ~ 1410 kg m^-3
• Core pressure of Sun (Chapter 16, pg 311):    dP/dr = - rg = - GM r/ R² which using scaling arguments is roughly P_c = GM <r>/ R ~ 2.7 x 10¹⁴ N m^-2
• Core temperature of Sun (Chapter 16, pg 312): P = rkT / mm_H =>
T_c = mm_HP_c / <r>k ~ 1.4 x 10⁷ K.

The virial theorem has a wide range of validity and usefulness. We can use it in problems concerning planetary orbits, stellar collapse, accretion disks around black holes, and motions in clusters of galaxies.

The real energy source of stars, of course, is nuclear energy.  An understanding of the nucleus was accomplished in the early and middle part of the 20th century.  Whereas energies involving chemical processes and excitations of electrons in atoms are of the order of 10 eV, nuclear processes involve energies millions of times larger (MeV).
• Elements are specified by atomic number Z (number of protons, or charge of nucleus).
• Isotopes of a given element are identified by weight A = Z + N, where number of neutrons N varies.
• e.g. Hydrogen has three isotopes, ¹H (one proton), ²H = deuterium (one proton and one neutron), ³H = tritium (one proton and 2 neutrons).


The energy contained in the nucleus is given by the rest mass of the nucleus,

E = mc².

Rest masses of an individual proton and neutron are very nearly the same:

m_p = 1.672623 x 10^-27 kg
m_n = 1.674929 x 10^-27 kg
but when combined into a nucleus their total mass is slightly less due to the binding energy.  The binding energy is just the energy required to split the nucleus into its constituent parts.  It is convenient to express nucleon masses in atomic mass units, which is defined as 1/12 of the mass of the Carbon-12 (¹²C) nucleus.
1 u = 1.660540 x 10^-27 kg
in which case the hydrogen atom (proton + electron) has a mass of m_H = 1.007825 u.  When protons and neutrons are combined into larger atoms in the cores of stars (in the process known as atomic fusion), their combined masses get smaller.  Thus, the total mass of four hydrogen atoms is 4.031280 u while after fusion into helium the atom has a mass of m_He = 4.002603 u., 0.7% smaller.  The difference in mass,
Dm = 0.028677 u,
represents an energy
DE =Dmc² = 26.71 MeV.
This energy is released during the process, and powers the energy output of the star.

Example:  How long will the Sun last if it shines at its current rate and converts 10% of its mass from hydrogen to helium in nuclear fusion?
 

E_nuclear = 0.1 x 0.007 x M_sunc² = 1.3 x 10⁴⁴ J.
t_nuclear = E_nuclear / L_sun ~ 10¹⁰ yr


which is more than enough time to account for the age of the solar system.