Nuclear Fusion Reactions

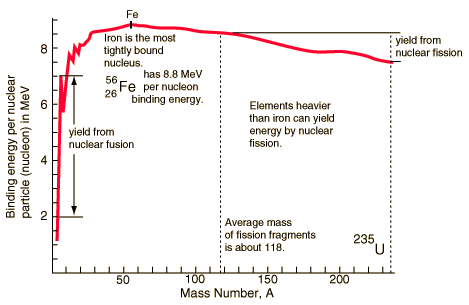
We just discussed the energy released when 4 hydrogen are fused into helium.  Each reaction requires that the strong electrostatic repulsion of the protons be overcome.  This requires high temperatures (so that the nuclei are moving rapidly) and high densities (so the nuclei are close together).  The process is aided by quantum mechanical tunnelling, where a particle has a finite probability of going through a potential barrier rather than over it.

The fusion of hydrogen to helium is accomplished not in one step, but through a chain of reactions called the proton-proton chain.  In fact, there are three different chains that lead to the same result, as shown below.  These occur in the Sun with the percentage shown in the table labels.
 
 

PP I Chain (69%)
	11H +		11H =>		21H + e+		+ ne
	21H +		11H =>		32He + g
	32He +		32He =>		42He +	2	11H

 

PP II Chain (31%)
	32He +		42He =>		74Be + g
	74Be +		e- =>		73Li + ne
	73Li +		11H =>		2 42He

 

PP III Chain (0.3%)
	74Be +		11H =>		85B + g		+ ne
			85B =>		84Be + e+		+ ne
			84Be =>		2 42He

A second, independent cycle called the CNO cycle also occurs to convert hydrogen to helium.  This cycle requires the presence of carbon, nitrogen and oxygen, but does not consume them.  They play the role of a catalyst.  Although the CNO cycle is not very important for the Sun, it is much more strongly temperature dependent than the PP chains, so it dominates for massive stars.  Most stars also convert He to C at some point in their lives, in a process known as the triple alpha process, and other, heavier elements are also "burned" inside stars as we shall see.

From Hyperphysics web page (http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html) by C.R. Nave, Georgia State University.

Because of the structure of the atomic nucleus, and the nuclear strong force that governs it, nuclei have an associated "binding energy."  To measure the binding energy, weigh a bunch of nucleons (protons and neutrons) individually, then put them together into a nucleus and weigh it.  The difference in mass, times the speed of light squared (E = mc2)  is the binding energy.  If we divide by the number of nucleons, we get the binding energy per nucleon.  This is shown in the above plot.  Note that iron (Fe) is at the peak.  This means that if we combine smaller nuclei into larger ones (nuclear fusion), we will gain energy up to Fe.  But beyond iron we actually lose energy.  Therefore, stars can gain energy through nuclear fusion up to Fe, but not beyond.  Note also that we can get energy from splitting the atom (nuclear fission) only if the original atoms are larger than Fe.  Note also that the amount of energy to be gained by fusion is far larger than by fission.  The atomic bomb works by splitting uranium.  The much more powerful hydrogen bomb works by fusing H into heavier elements.

Energy generation in stars can be parametrized by an energy generation rate, e (J s^-1 kg^-1), so that the luminosity contributed by a mass dm is

dL = edm.

For a spherically symmetric star, a spherical shell of width dr has a mass dm = r dV = 4pr²rdr.  The radial variation of luminosity (energy/s) within the star is then

dL / dr = 4pr²re.                (5)

The energy generation rate is just the sum of the rates of all applicable processes, so it has a contribution from each branch of the PP-chains, from the CNO cycle, and from gravity.

Energy is generated by both gravity (throughout the star) and nuclear reactions (in the core), but most of the energy by far comes from the core, where the temperatures and densities are high enough to allow fusion to take place.  This energy must then find its way to the surface of the star, to be radiated away.  There are three main ways for energy to be transported:

• conduction (efficient only for solids and liquids, not for gases)
• convection (boiling)
• radiation (photons)

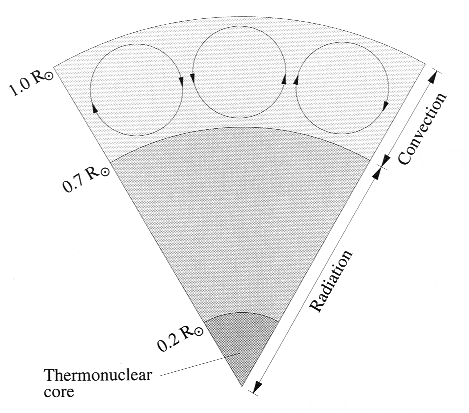
Schematic diagram of the interior of the Sun, showing regions of thermonuclear burning, energy
transport by radiation, and energy transport by convection.  Other stars have different details,
but the same basic structure applies.  Figure from Carroll and Ostlie, Introduction to Modern
Astrophysics, Addison-Wesley, New York, 1996.

The latter two mechanisms are competing mechanisms in stars.  Convection occurs when the temperature falls rapidly with height (a steep temperature gradient, dT/dr).  Imagine a rising parcel of gas--as it rises it expands (because the outside pressure drops).  It also cools due to the expansion (adiabatic expansion), but if the temperature of the outside surroundings falls even faster then it will be buoyant.  This situation is then unstable and the parcel of gas will continue to rise.

When the star has a shallow temperature gradient, it is stable to convection and the only mechanism left is radiation.  Then the photons carry the radiation, but they carry it very slowly.  Photons take 10⁶ years to reach the surface of the star!

Most stars, including the Sun, have radiative cores and convective envelopes.  The Sun is convective from 0.7 R_sun to the surface.  We see that whether stars carry energy by radiation or convection depends on the way that temperature varies with radius in the star.  How does the temperature vary within the star?  Except where it is generated in the core, each layer of the star merely transports energy.

For radiation, the flux of energy is F = sT ⁴, so the flux through a thin spherical shell of thickness dr due to flux coming from below is just

dF = sT ³dT .    (Note that if dT = 0 then dF = 0; flux in = flux out)

The fact that the temperature drops as we go out from the center of the star is due to the gas absorbing energy to maintain its temperature.  The absorption is

dF = -k(r) r(r) F(r) dr .    (where k(r) is the absorption coefficient)

Combining these, and using F(r)= L(r)/4pr ², we have

L(r) = -[16pr ²sT ³ / k(r) r(r)] dT / dr

The full machinery results in an additional factor of 4/3, so that the temperature gradient is

dT / dr = -[3k(r) r(r) / 64pr ²sT ³ ]  L(r)                (6)

When the absorption, k(r) r(r), gets too large, convection takes over.  When energy is carried by convection, a different expression for the temperature gradient results:

dT / dr = (1-1/g) [T(r)/P(r)] dP(r)/dr               (7)

Combining equations (4) - (7) and the equations of hydrostatic equilibrium and the ideal gas law, we have a complete set of coupled differential equations that can be solved with the help of computers to determine the structure of the interior of stars.  Different stellar structures can be investigated by changing the initial parameters of mass and composition.  Such models are key to understanding the evolution of stars.