Introduction

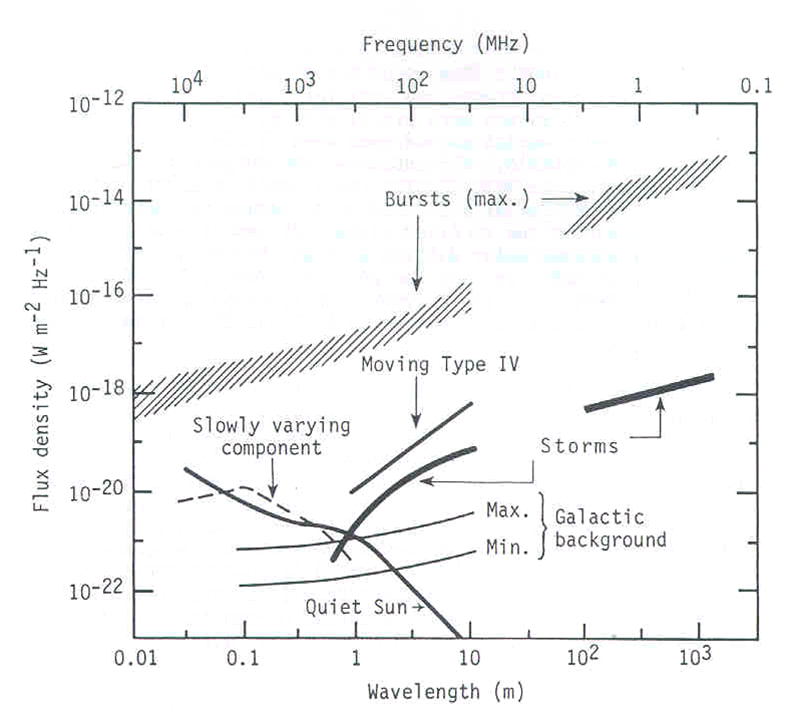
We have basically covered the main issues one needs to know to understand how radio emission is produced, how it is measured with modern instrumentation, and how that instrumentation works.  For the next three lectures we will look at some of the science that has been and can be done using radio astronomy techniques.  We start with the Sun, since this object dominates the radio sky, and offers a laboratory to investigate the main types of radio phenomena at a high level of spatial and spectral detail.

Before launching into the radio science itself, it will be helpful to look briefly at the structure of the Sun.  The Sun is a normal star of spectral type G2V, which means that it is burning hydrogen in its core, as it has been doing for the last 5 billion years, and as it will continue to do for about 5 billion years more.

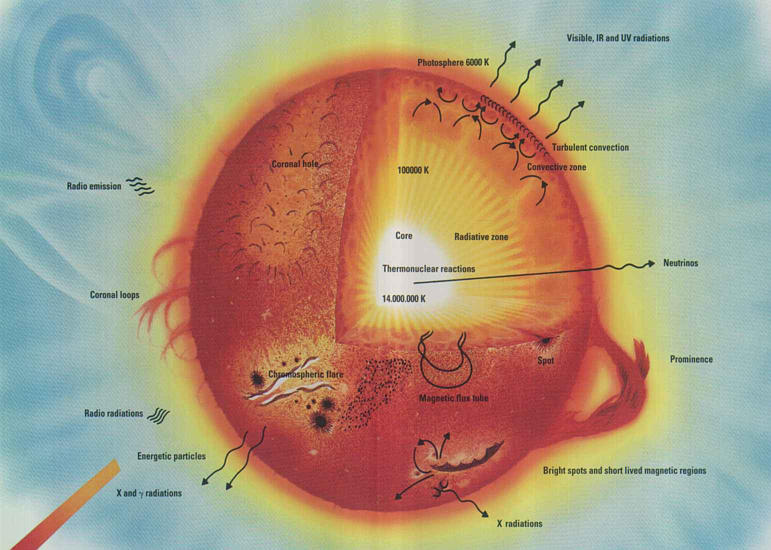
Figure 1:  A schematic view of solar structure

The core temperature is about 14 million K, and the temperature falls off with distance from the core, eventually reaching the surface temperature of 5800 K.  The photons generated in the core take about 1 million years to reach the surface, since they propagate outward in a random walk with a very short mean free path.  Their point of last scattering is in the photosphere, after which they are finally free to stream out into space.  Because they are in thermal equilibrium with the photosphere, they have a pure blackbody spectrum corresponding to the 5800 K temperature, but en route to space they encounter the more tenuous gas of the other layers of the solar atmosphere--the temperature minimum region, the chromosphere and the corona--so the solar spectrum shows many spectral lines.  The fact that these lines are mostly absorption lines tells us that the temperature falls to yet lower values above the photosphere, to about 4500 K in the temperature minimum region.  This is fully expected, but what is surprising is that above this height the temperature rises again, and in fact rises very steeply at about 2000 km above the photosphere to form a very hot (several million K), very tenuous plasma that we call the corona.  The figure below shows the temperature profile starting just below the photosphere, through the temperature minimum region, the chromosphere, and the abrupt increase leading to the corona.

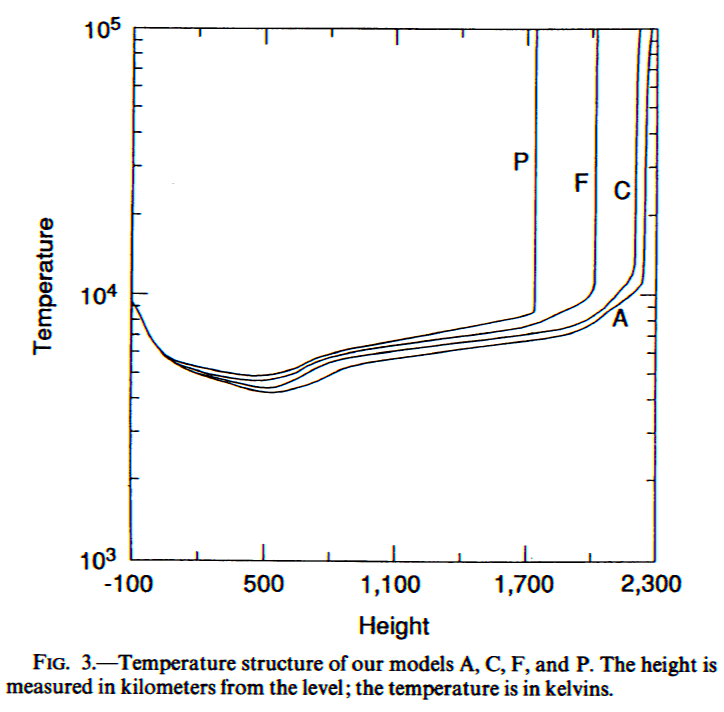
Figure 2: From Fontenla, Avrett & Loeser (1993)

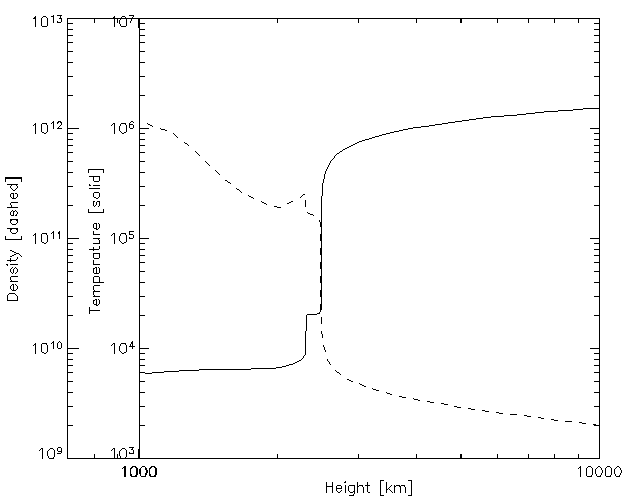
Figure 3: A similar plot to that of Figure 2, showing the temperature and density
(for an older model showing the now discredited "Lyman α Plateau").

The appearance of the "quiet time" solar atmosphere at radio wavelengths is governed by the plasma parameters (temperature, density, and magnetic field strength) and the radiation mechanisms that generate the radio emission (free-free emission, gyroresonance emission, and plasma emission).  The following figure shows the height versus frequency of three characteristic frequencies that we have already met--the plasma frequency, the gyrofrequency, and the frequency at which free-free emission reaches optical depth unity.

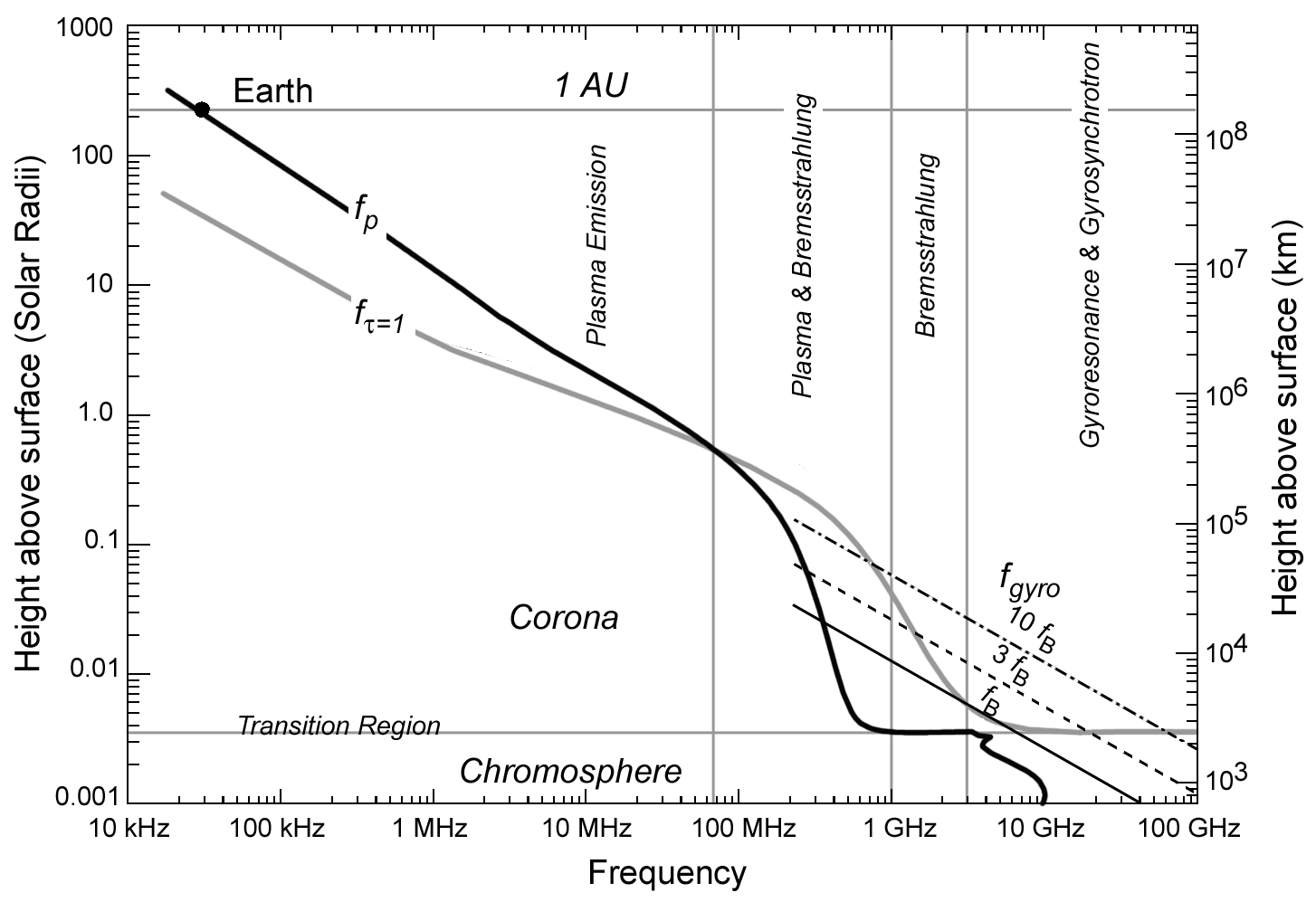
Figure 4: The highest curve in this plot specifies the type of emission mechanism that will dominate at
different frequencies in the solar atmosphere.  The curves are based on the dependence of different
emission mechanisms on the plasma parameters of temperature, density, and magnetic field strength.
The plot covers 7 orders of magnitude in frequency, and in height in the solar atmosphere.

Here is an animation showing the different appearance of the full Sun as a function of frequency.  In reality it is only a set of four images, taken at the highest available resolution, with the images morphed from one image to another to give the impression of a large set of frequencies.

Because of the huge increase in electron density at the chromosphere, radio emission becomes optically thick due to free-free emission at heights higher than the solar minimum region, even at the highest frequencies.  Therefore, radio observations pertain only to the upper chromosphere and higher.  Let us start at the chromosphere and move outward in the solar atmosphere.  As Figure 4 shows, this is also equivalent to starting at the highest frequencies and moving to lower frequencies.  The figure below shows the Sun at very high (sub-mm) frequency.

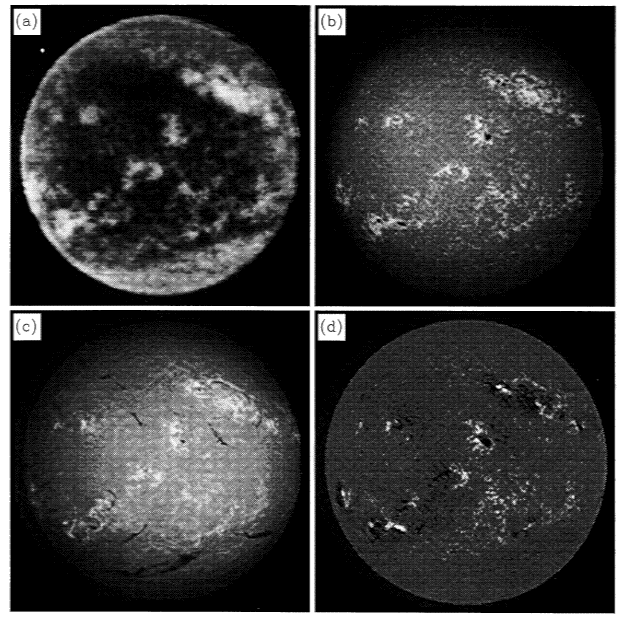
Figure 5: (a) The Sun at 850 microns wavelength (>300 GHz), showing the low
contrast of features in the low chromosphere.  The brightest features have a
brightness temperature of about 6500 K, and the darkest features have a brightness
temperature of about 5500 K.  The other panels show (b) Ca II, K-line image,
(c) H-alpha, and (d) a magnetogram, for comparison.  From Bastian, Ewell, & Zirin (1993).

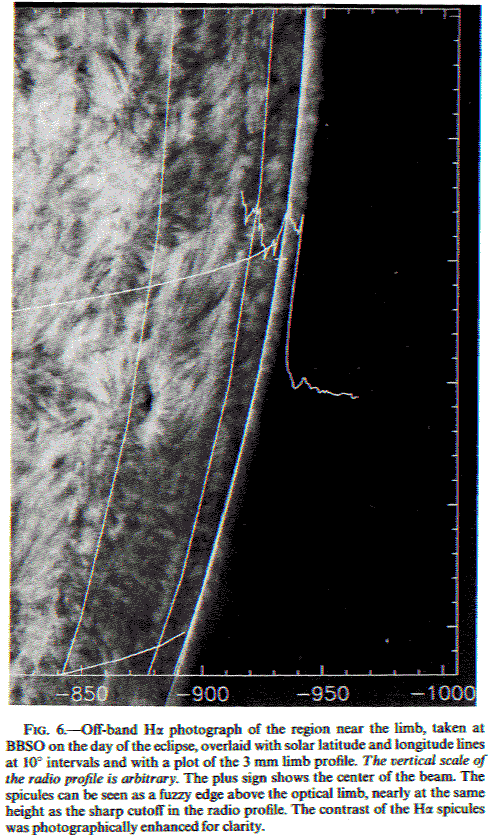
The figure below shows how the height of the radio Sun at 3 mm wavelength extends well beyond the visible edge (photosphere), and matches quite well with the tops of the spicules.  This is from Belkora, Hurford, Gary and Woody (1992).

Recent work has called into question the existence of a stationary temperature profile in the chromosphere, such as those indicated in Figures 2 and 3.  This idea is spurred observationally by the fact that very cool regions of the atmosphere appear to exist in which CO (carbon monoxide) lines are seen.  It is also suggested by time-dependent, dynamical models.  Carlsson and Stein (1995) give the following plot showing a time-averaged "chromosphere" and the actual range of time-variable dynamical temperatures that went into the average.

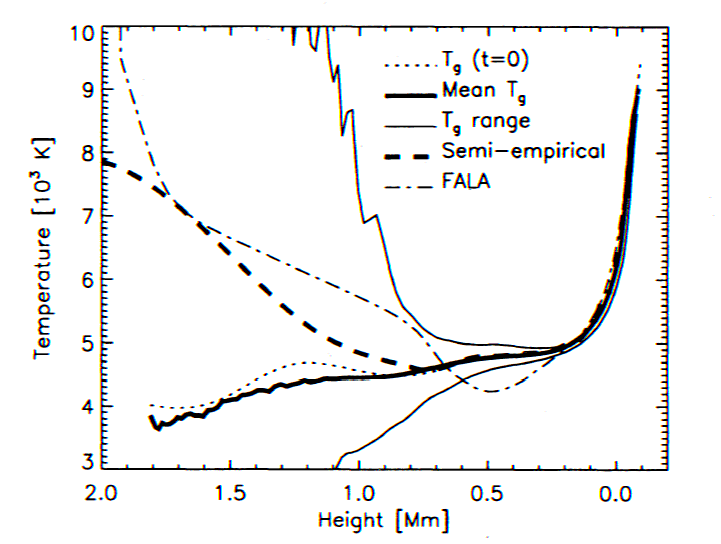
Figure 7:  A comparison of the FAL model A with some temperature profiles of the
lower solar atmosphere derived from time-dependent wave heating models of the
chromosphere.  The two thin solid curves show the extremes of temperature, while
the thick line shows the time-averaged profile.  The dot-dashed line is the FAL A model.

The chromosphere is dominated by the supergranular structure--large-scale convective cells of order 30" (200,000 km) in size.  The gas rises in the center of the cells, moves to the edges, and descends.  As a result, it tends to sweep relatively weak magnetic fields to the edges, where it collects to form the chromospheric network structure.  Radio images show a good correspondence of the radio sources with the magnetic elements, as shown in Figure 8.  Quantitative results are frustrated by the fact that such images from the VLA require an all-day (8-12 hour) synthesis, and so time-variability cannot be easily followed.  There is some evidence that the individual magnetic elements "flicker" in brightness.

Figure 8: The panel on the left shows the radio image at 8.5 GHz (3.6 cm wavelength), showing the
network struction.  The corresponding magnetogram on the right shows a high degree of agreement,
with each source overlaying a magnetic element of the chromospheric network.  The feature marked
with a "d" is the only one representing a magnetic dipole.

One still unresolved puzzle about the chromosphere is why at some frequencies (at least 10-100 GHz) the polar coronal holes appear brighter than the rest of the quiet Sun.  There is some evidence that all coronal holes, even those not at the poles, are brighter.  This means that the temperature of the lower chromosphere (that sampled by this range of frequencies) is greater at an equivalent optical depth.  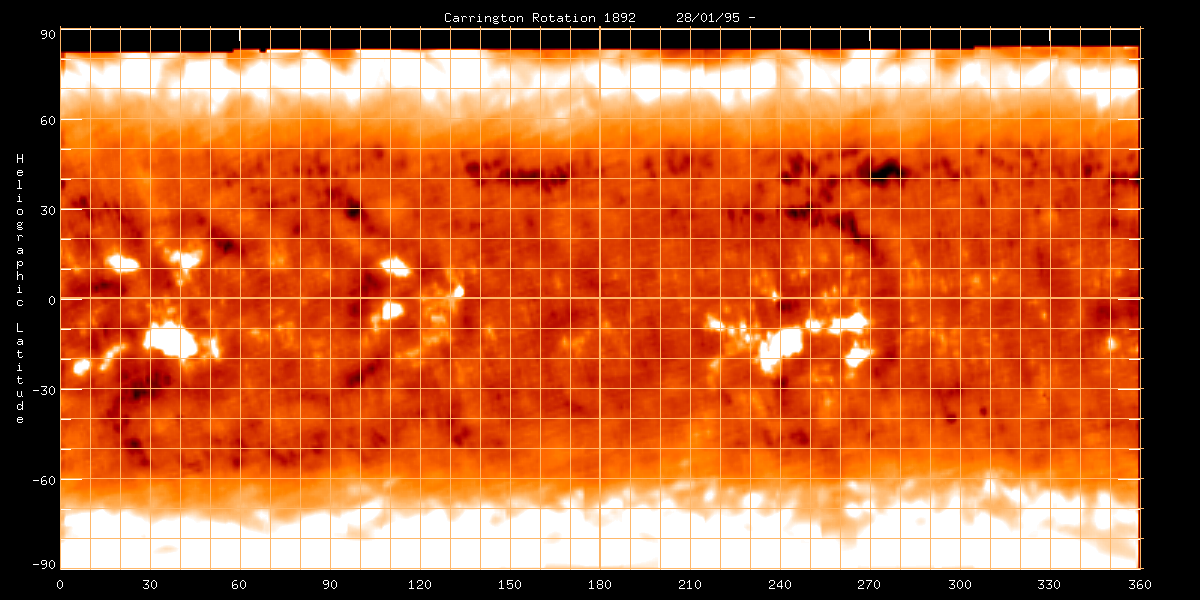Meanwhile, coronal holes are darker than the rest of the quiet Sun at lower frequencies.  Here is a synoptic chart showing this effect at 17 GHz, from Nobeyama.  The contrast in this image is enhanced, but the excess brightness is really only about 500-1000 K.

In addition to the ability of radio emission to give the temperature of the chromosphere, it can also tell us something about the magnetic field strength, derived from the magnetic field dependence of the polarization.  Recall that free-free emission opacity was given in Lecture 3 as:

κ_ν = (1/3c)(2π/3)^1/2(ν_p/ν)²[4πn_eΣ(n_iZ_i²)e⁴/m_e^1/2(kT)^3/2]G_ff(T,ν)
     = 9.78 x 10⁻³n_eΣ(n_iZ_i²)/ (ν²T^3/2)                                                              (1)

 

x {	18.2 + ln T3/2 − ln ν      (T < 2 x 105 K)
	24.5 + ln T − ln ν         (T > 2 x 105 K)

However, this expression does not include the effect of the magnetic field.  That can be included by changing the frequency from ν to ν + σν_B |cos θ|, where ν_B= 2.8x10⁶ B is the electron gyrofrequency, θ is the angle of B to the line of sight, and σ is +1 for o-mode, and -1 for x-mode.  The expression (1) then becomes:

κ_ν= 9.78 x 10⁻³n_eΣ(n_iZ_i²)/[(ν + σν_B |cos θ|)²T^3/2]                                                          (2)

x {	18.2 + ln T3/2 − ln ν      (T < 2 x 105 K)
	24.5 + ln T − ln ν         (T > 2 x 105 K)

where we ignore the slight dependence on ν_B in the logarithmic term.  Recall that in order for free-free opacity to be important relative to gyroresonance opacity, we must have ν > sν_B, where s is typically 3 or 4, otherwise gyroresonance opacity will dominate.

When we observe the chromosphere in the two senses of circular polarization (R and L), the expression is the same as (2), but without the absolute value on the cos θ term.  In other words, a given mode (i.e. x-mode), can correspond to either R or L polarization, depending on the sign of B.

Now, recall that for optically thin emission,

T_b = T_eτ = TκL.

We can express the degree of polarization as

P = (T_R−T_L)/(T_R + T_L) =  (κ_R−κ_L)/(κ_R + κ_L) = (2ν_B/ν)cosθ.                                  (3)

Thus, the degree of polarization is directly proportional to longitudinal (line-of-sight) component of magnetic field strength, B_l = B cos θ.  This gives a means to measure relatively weak magnetic fields in the chromosphere.  Unfortunately, there is one more complication, because in fact the chromosphere is not optically thin.  One might expect, then, that this would eliminate any net polarization, but note that the two modes become optically thick at different depths.  This is shown in Figure 10, which is just a repeat of Figure 2 with an overlay that shows how, with no magnetic field, a particular frequency may become optically thick at the height indicated by the dashed black arrow.

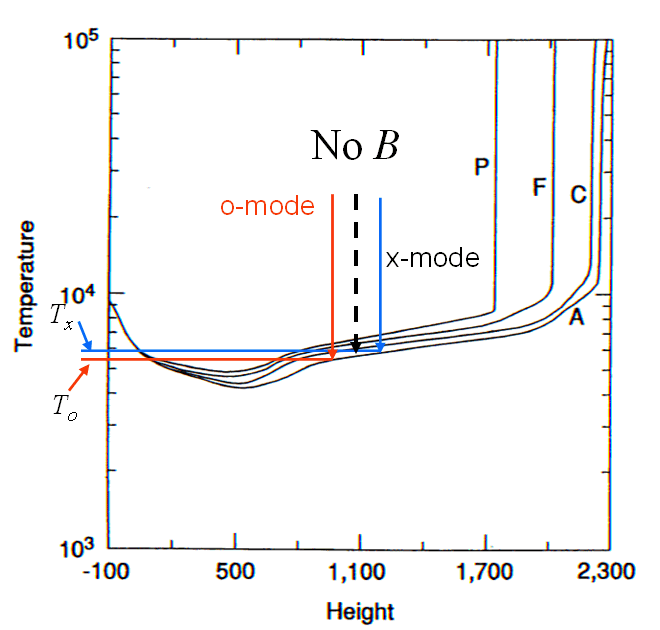
Figure 10: Repeat of Figure 2, schematically showing how different opacities in o- and x-mode give rise
to different brightness temperatures and hence gives a net polarization. As B_l increases, the red and blue
arrows separate and the temperature difference increases, increasing the net polarization.

In the presence of a magnetic field, the greater opacity in x-mode (blue arrow) means it becomes optically thick higher in the chromosphere than the o-mode (red arrow).  Due to the temperature gradient in the chromosphere, the brightness temperature of the two modes is different (x-mode has a higher brightness temperature as shown by the blue and red horizontal lines in the figure), so there is still a net polarization.  Now, however, the polarization is due to the mode-dependence of the brightness temperature due to the temperature gradient, so we need a way to get the otherwise unknown temperature gradient.  Luckily, if we have the brightness temperature measured at many frequencies one can use the slope of the radio spectrum, which itself is related to the temperature gradient.  In fact, if the brightness temperature spectral index is written as n, then the expression (3) becomes

P = (nν_B/ν) cos θ,                                  (4)

which is a general expression since for an isothermal plasma the optically thin spectral index is n = 2, for which (4) reduces to (3).  Can we really measure magnetic fields in this way?  We do not really know at present, because we have not had an instrument capable of the required observations.  We need excellent imaging to map the complicated structures of Figure 8, but we also need the images at many closely spaced frequencies to determine the spectral index.  That is one motivation for building the Frequency Agile Solar Radiotelescope (FASR), which for the first time will have the required combination of imaging and spectral capability.

As we go higher in the solar atmosphere, the temperature rises steeply to millions of K, while the electron density falls greatly.  This hot, tenuous plasma was first discovered through radio observations, was quite unexpected, and still remains unexplained.  There have been many theories to try to explain it, such as wave energy coming from the surface and being deposited in the corona, but none of these theories seem to work.  A favored mechanism now is dissipation of magnetic energy through many small flares (microflares), but current estimates show that there is not enough energy released in the visible events to account for the hot corona.  There remains the possibility that even smaller events (nanoflares) might supply the needed energy, but so far they have not been shown to rise steeply enough in numbers to account for the needed energy.

The corona is everywhere hot, but certainly is hottest in active regions, which are regions associated with sunspots.  Here we see that microflares and larger flaring events tend to concentrate, and it shows that flares are closely related to magnetic fields, that get stressed due to motions and new flux emergence to provide energy for the sudden releases that we call a flare.  However, many aspects of this release of energy are still unknown.  We will discuss flares and solar activity in the next lecture.  For now, let's look at the general structure of active regions.

Solar and Galactic Background Flux Density

Before we leave this lecture, let's briefly discuss the flux density levels of the two strongest sources in the sky, the Sun and the Galaxy. Figure 11 shows this for various states of solar activity as a function of frequency (scale along the top of the figure) and as a function of wavelength (scale along the bottom). The gap between 10 and 100 m wavelength corresponds to the frequency cutoff due to the ionosphere (10 m, or about 30 MHz), and the low frequencies observed from space, which at the time of this figure were limited to about 2 MHz or less. Spacecraft measurements have now closed the gap (going up to 15 MHz with the Wind spacecraft), and the curves shown with gaps actually join together rather continuously. At quiet times, the quiet Sun dominates down to about 1 m wavelength (300 MHz), but below that the galactic background dominates. The curve labeled Slowly Varying Component basically means active regions, which may slightly dominate the quiet Sun in flux density, but rather strongly dominate in terms of brightness temperature. At times of storming activity and outbursts, the Sun can dominate strongly at all frequencies, being 4 or 5 orders of magnitude above the quiet Sun at lower frequencies.
 

Figure 11: The overall background flux of the galactic background and the Sun at various activity levels.