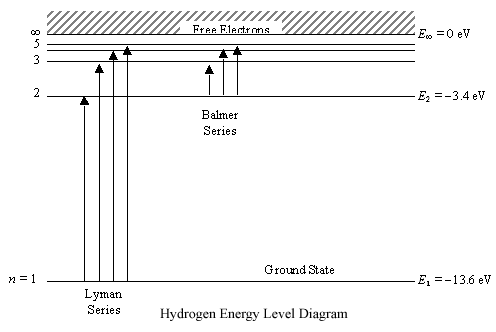
- 1/lab
= nab/c
= (Eb -
Ea)/ch=RH[1/nb2-1/na2]
Use na=110, na=109 to get
- nab
= RHc[1/1092-1/1102]
= 1.5 x 10-6RHc
= 5 x 109
Hz.
| Physics 728 |
|
Prof. Dale E. Gary
NJIT |
Radio Emission Mechanisms
Types of Radio Emission Mechanisms

Use na=110, na=109 to get
Radio recombination lines arise in HII regions, which are regions of the interstellar medium where the ordinarily neutral hydrogen gas is ionized by a nearby hot star, whose light is rich in UV photons. The UV photons ionize the atoms, and the electrons recombine and cascade downward toward the ground state. Some fraction (given by the Boltzmann and Saha equations) make the transition from 110 to 109, and emit a 5 GHz photon. Although the density of the interstellar medium is low (perhaps 104cm-3), the path length is long (~0.5 pc), so the emission can be observed as a weak radio line. Note that transitions around H40a are in the 100 GHz (millimeter) range, and around H600a are around 30 MHz range, so the entire radio spectrum can provide recombination lines.
An important question is how broad are these recombination lines? The "natural" width of lines is the inverse of their lifetime (how long they stay at one level before transitioning to the other level). These lifetimes are rather long, so the intrinsic width of the lines is narrow (about 0.1 Hz!, see here). However, their observed width is mainly due to "Doppler broadening" resulting from motions of the atoms. This could be due to a combination of thermal motions and turbulent motions. The level of turbulence is not generally known, but the thermal broadening can be calculated based on an estimate of the temperature of the population of emitting atoms and any excess broadening can be ascribed to turbulence.
For a thermal (Maxwellian) distribution, the distribution of speeds of the atoms is determined uniquely by the temperature, and a concise derivation of the thermal doppler width can be found here. The result is given as
By studying these recombination
lines, we learn the following about HII regions:
Hyperfine
Splitting and the 21 cm line
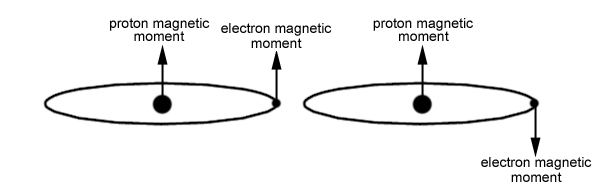
Another important transition is
not a transition from one principle quantum state to another, but rather a
spin flip of electrons in neutral hydrogen atoms. The ground state of
hydrogen has slightly different energies for electrons with spin parallel
and antiparallel to the proton, as shown below:
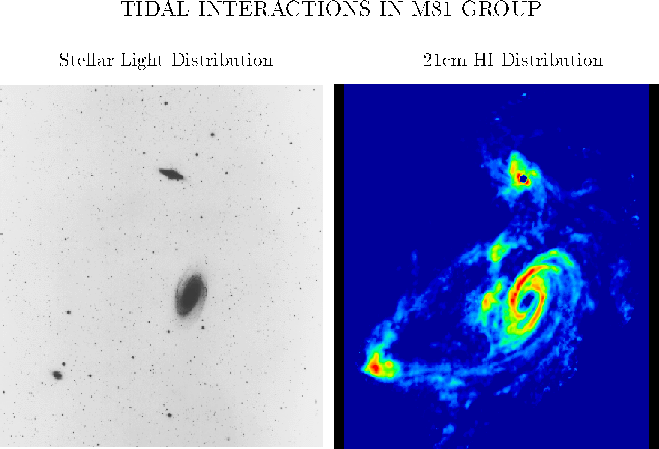
Neutral hydrogen traces interactions
among galaxies in the M81 group.
(c) National Radio Astronomy
Observatory / Associated Universities, Inc. / National Science Foundation
By studying the 21 cm line, we
learn the following:
Consider a diatomic molecule such as CO, or O2, or H2. They can spin along different orthogonal axes, such as along the line joining the atoms, or perpendicular to this line. They can also vibrate. Under quantum mechanical rules, these rotational or vibrational modes are quantized, as you learned in Statistical Mechanics. The general idea can be developed using classical physics, e.g. consider the molecule as a "bar-bell" as shown below, spinning on the axis shown.Free-Particle EmissionThe rotational kinetic energy is just E = 1/2 I w2, where I = mr2 is the moment of inertia, and m = mM / (m + M) is the reduced mass, as before. Thus, E = 1/2 mr2w2. But in quantum mechanics, the angular momentum L = I w is quantized according to angular momentum quantum number J, |L| = [J(J+1)]1/2 h/2p, so we find that w2 = L.L / I2= (h/2p)2 J (J + 1) / m2r4and finallyE = (h/2p)2 J (J + 1) / 2mr2 .It is straightforward to show that the rotational transition J = 1 to 0 of the CO molecule results in a spectral line at frequency 115.2712 GHz, while the J = 2 to 1 transition gives a line at 230.5424 GHz, given that the intermolecular bond distance is 1.128 A. These are but two of many molecular lines that can be detected from clouds in interstellar space and in other galaxies to provide information on the distribution of cold, dense matter. Note that CO and other molecules are easily dissociated by radiation and collisions by hot gas atoms, so its presence implies very cold conditions. Typically molecular clouds have temperatures of order 100 K, and sometimes as cold as 10-30 K. They are associated with dust clouds, and it is the dust that protects the fragile molecules and helps to cool the cloud by radiation of IR.
Image of M16 (Eagle Nebula) molecular cloud and star-forming region. From HST web site.
The emission types that we have discussed up to now are transitions between bound states, for which quantum mechanical rules are of the first importance. However, for astrophysical plasmas in a high-energy environment, such as in stars, or the tenuous atmosphere around stars, it is free particles that dominate the radio emission mechanisms. (Note that bound state transitions can still be important at UV and soft X-ray wavelengths in such high-energy plasmas.) This includes all radio emission from the Sun and in the interplanetary medium, including the Earth's magnetosphere and ionosphere.Coherent Free-Particle EmissionRecall that a charge at rest or in uniform motion (in the non-relativistic limit) has an electrostatic electric field (cgs units):
E = q/r2 r,which is a radial field falling off as 1/r2. The power radiated is the square of the electric field, so the power from the radial part of an electrostatic field vanishes quickly, as 1/r4. However, when a transverse "kink" appears in the field, that transverse part falls off only as 1/r, so the power falls off as 1/r2. So any phenomenon that produces a kink in the field will result in radiation. The typical way to produce a kink in the electrostatic field of a charge is to accelerate the charge.The Larmor Formula (see Jackson, 2nd edition, section 14.2) expresses the radiated power from an accelerated charge per unit solid angle as:
dP/dW = q2a2 sin2 q / 4pc2 (1)where q is the charge, a is the acceleration, and q is the angle from the direction of the acceleration. Note that the "radiation pattern" is a dipole pattern, which looks like this:and the pattern arises naturally from the geometry. A dipole antenna (where charges travel in simple harmonic motion up and down the antenna) has exactly this radiation pattern. In the case of relativistic motion of charged particles, the pattern is altered, as we will discuss shortly (see Jackson, 2nd edition, section14.3). To get the total power radiated, simply integrate (1) over all solid angle to get P = 2/3 q2a2 / c2. What kind of charged particles are good at radiating? Note that the force required to produce an acceleration is F = ma, so the acceleration is a = F/m, and dP/dW ~ 1/m2. So electrons are better at radiating than protons by a factor (mp/me)2= 4 x 106 ! For radio emission, we can assume that the only particles important for the emission are electrons.
Cherenkov Emission
For completeness, we briefly mention that the velocity of a free charge moving in a medium can actually exceed the speed of light in the medium. This causes the light to radiate in a cone, exactly like sound waves from an aircraft that exceeds the speed of sound. This effect gives rise to Cherenkov emission, which is responsible for the blue glow given off by nuclear reactors that are surrounded by water, and for emission by cosmic rays in the Earth's atmosphere. This is one of the few mechanisms that can result in radiation without the need for the particle to accelerate. Cherenkov emission plays no role in radiation in plasmas, however, because the wave speed of light in an ionized medium is greater than c!Bremsstrahlung
This is an important type of radiation in many astrophysical plasmas. The word is german for "braking radiation," as is due to accelerations caused by collisions between electrons and ions (Coulomb collisions). Recall that the Coulomb force is F = qE, so the force on an electron in the electrostatic field of a proton is an attractive force F = -e2/r2r. In head-on collisions, the electron can actually bounce off the proton, and lose most of its energy, or even reverse its direction. In this case, the energy of the photons emitted is typically in the X-ray range. The hard and soft X-rays from astrophysical plasmas, including the Sun, are a mixture of bound-bound atomic transitions (soft X-rays), nuclear line emission (hard X-rays/gamma rays), and electron bremsstrahlung. In the hard X-ray range (10-1000 MeV), the emission is purely electron bremsstrahlung.Radio emission, in contrast, is due to relatively gentle, distant collisions of electrons with ions. Picture the plasma as a soup of electrons and ions, with the electrons zipping around at great speed through the relatively immobile ions. The path of an electron is continually wiggling due to slight deviations as it passes each ion, and each wiggle produces radiation in a broad spectrum (related to the energy lost or gained in each collision). Note that in the case of local thermodynamic equilibrium (LTE), the electron is also absorbing radiation in approximate equality with its energy loss. We will only discuss emission today, but will discuss absorption next time.
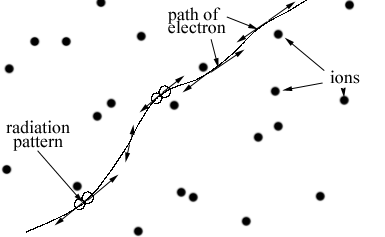
An electron moving through relatively immobile
ions experiences many small accelerations, each
one producing a radiation pattern along its direction
of motion (perpendicular to its acceleration).Let us look a bit more closely at a single collision. As shown in the figure below, the electron experiences a deviation of its straight line path by an angle q, which depends on the speed of the electron and the distance of the encounter, which is called the impact parameter, b. Bremsstrahlung has the peculiarity that the amount of deviation (and hence the power radiated) is actually greater when the electron is moving more slowly, and smaller when v is high. We will see this when we get to the final form of the emissivity.
One can calculate the emission from this process, but it is rather involved (see Rybicki & Lightman, "Radiative Processes in Astrophysics," 1979; or the web discussion here.). The outline of the procedure is to use the small-angle-approximation, for which the electron deflection is negligible, and consider the motion along a straight line, where the separation between charges is r = (b2 + v2t2)1/2. One uses the dipole approximation to determine the net acceleration over the path, and thus the emission from a single electron for a single collision
dW(b)/dw = 8Z2e6/(3pc3me2v2b2), for b << v/w. (2)Note that this depends on the impact parameter b, and we limit the solution to b << v/w because collisions at a given b lead to emission only at w < v/b. To extend this to a volume flux of electrons, all with speed v, note that the rate of collisions on any one ion is just nev, and these electrons will fill the area with element of area 2pb db. Then the total emission (energy) per unit time per unit volume per unit frequency range is
dW bmax dW(b) = neni2pv b db (3) dwdVdt bmin dw where the limits of the integral over impact parameter depend on the case to be evaluated. For any emission, there is a reasonable upper limit, where bmax = v/w. For radio emission (where the collision energy should be relatively low), we can take a lower limit as for a 90o deflection, which occurs for bmin = 4Ze2 / pmev2. For higher-energy emission (i.e. X-rays, with head-on collisions), a smaller impact parameter should be taken. When (2) is inserted into (3), we obtain
dW bmax db = 16e6neniZ2/(3c3me2v) dwdVdt bmin b = 16e6neniZ2/(3c3me2v) ln (bmax/bmin).
It is conventional to write this as
dW / dwdVdt = 16pe6neniZ2/(33/2c3me2v) Gff(T,w), (4) where Gff(T,w) is the Gaunt factor:Gff(T,w) = (31/2/p) ln [p(kT)3/2 / 21/2Ze2me1/2 w]. (c.f. Dulk 1985). where we have made the assumption that the electron velocities are the thermal velocities,
v = (2kT/m)1/2. Gaunt factors for many other cases can be calculated exactly (see Figure 5.2 of Rybicki and Lightman 1979).Thermal Bremsstrahlung
The last step is to integrate the emissivity over a population of electrons, and in most cases for radio emission this is done explicitly for a thermal distribution (that is, the velocities are distributed according to a Maxwellian distribution). In other words, integrate (4) over all velocities. Let us use the symbol hn in place of the unwieldy dW / dndVdt, which we call the emissivity. Then after integrating (and converting from w to n) we get:hn = (26pe6/3mec3)(2p/3mekT)1/2 neniZ2 Gff(T,n).Note that for the solar corona, neniZ2 ~ ne2, so the emissivity depends on the square of the electron density, and is inversely proportional to temperature (emissivity goes down for higher temperatures!). Also note that there is almost no frequency dependence--the only dependence is the weak (logarithmic) dependence in the Gaunt factor. We will see next time, when we introduce the absorption coefficient, that this is only true when the emission is optically thin.
It is important to recognize that the mechanism of Bremsstrahlung is not defined solely for a thermal distribution of particles (it is a common mistake to assume so). Calculation of Bremsstrahlung for other types of distribution is still a research topic, e.g. the recent paper by Fleishman and Kuznetsov (2014), which discusses emission from the kappa distribution and the n-distribution.
Gyroemission
There is another way to accelerate free particles, by considering the effect of the magnetic field and looking at the magnetic part of the Lorentz force F = qE + (q/c) v x B. For a plasma, there is usually no macroscopic electric field (except perhaps in current sheets), but often there is a non-negligible magnetic field (in which case the plasma is termed a magnetized plasma). In this case, an electron of speed v will be accelerated perpendicular to both v and B, with magnitudea = evperpB/mec in the right-hand-rule sense (because charge is negative), as shown in the following figure: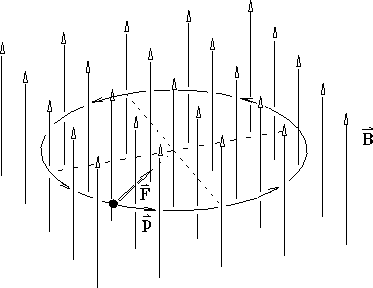
Put the thumb of your right hand in direction of B, and an electron (negatively charged)
will gyrate in the direction of your fingers. A proton gyrates in the opposite direction.Again, one can calculate the emission from this process, and again it is beyond the scope of this course. However, from the Larmor formula you can see that the power radiated will be
P = (2e2/3c3)(e2B2/me2c2) v2perp, for the non-relativistic case. For the relativistic case, this formula should be multiplied by g2. Some of the properties of this emission, which will be very important for understanding solar emission from both active regions and flares, are:
- Cyclotron emission: In the non-relativistic case (low electron velocity, i.e. low temperature), the electrons gyrate at a fixed frequency, independent of their speed, called the gyrofrequency wB = eB/mec, which depends only on magnetic field strength. The emission from a single electron, when viewed from afar, has a radiated power that varies sinusoidally, which gives rise to a cyclotron line at the gyrofrequency, fB = eB/2pmec = 2.8 x 106 B Hz (B in gauss).
- Gyroresonance emission: At slightly higher electron velocity (T ~ 105-106 K), a relativistic effect comes in that changes the sinusoidal dipole pattern to a slightly asymmetric shape,
so that the radiated power peaks more strongly. This gives rise to harmonics of the cyclotron line (so-called gyroresonance lines),
f = sfB = seB/2pmec = 2.8 x 106 sB Hz (s = 1, 2, 3, ...). This type of emission is responsible for bright coronal emission from solar active regions.
These characteristics are for a single electron, or by extension a mono-energetic population of electrons. To determine the expected emissivity from a plasma, one must integrate the contribution of emission over a particular velocity distribution of electrons. There is a lot of effort in trying to determine an appropriate distribution to use for a given situation, and this is an area of active research. Typically there are two types of population that we consider: a thermal population (in which case the emissivity is expressed in terms of plasma parameters T, ne, and magnetic field parameters B andq), or a powerlaw distribution in energy (in which case the emissivity is expressed in terms of energy distribution parameters N, d, and perhaps Eo, and magnetic field parameters B andq).
- Gyrosynchrotron emission: At mildly relativistic speeds (electron energies 100-300 keV), the effect becomes stronger, and the lines go up to harmonics 10-100. The lines also become broader (thermal broadening), so that they blend together into a continuum emission. This form of the emission is called gyrosynchrotron emission, and is the type of emission responsible for most radio emission from solar and stellar flares.
- Synchrotron emission: At highly relativistic speeds, the forward lobe becomes a narrow beam of width 1/g3, and the emission comes in narrow pulses at the cyclotron frequency, beamed along the direction of motion. The pulses contain many many harmonics. This kind of emission is important in extreme energy environments such as black holes, neutron stars, and some extragalactic sources (generally associated with black holes).
In some cases, such as thermal gyroresonance emission, or synchrotron emission from an isotropic powerlaw distribution, the emissivity can be written down analytically. A good overview is given by Dulk (1985). Here is the emissivity in these two cases:
Gyroresonance emissivity for a thermal distribution of electrons:
hn(s,q) = p2me/4c [msd(wms)/dw]-1b2nnp2(s2/s!) [s2b2sin2q /2]s-1[b cos q]-1
x exp[-(1 - snB/n)2/2 ms2b2cos2q)](1 -s|cos q|)2Synchrotron emissivity for a powerlaw distribution of electrons:
Transition Radiation
hn/BN = 1/2 (d - 1) Eod - 1 g(d) 31/2e3/8pmec2 sin q [(2me2c4/3 sin q) n/nB]-(d - 1)/2
To round-out our discussion of radio emission mechanisms from free particles, it is worthwhile to point out a relatively new mechanism proposed for astrophysical plasmas, although it is a well-known mechanism in devices. This mechanism shares one characteristic with Cerenkov emission, in the sense that no acceleration is required to produce the emission. Instead, the transverse component of the electric field is produced by an inhomogeneity in the refractive index of the medium. To understand how the mechanism works, recall that the electrostatic field of a charged particle radiates outward with the group speed of light in the medium. Slight irregularities in these radiated field lines will occur when the group speed is not uniform. The mechanism was originally considered for the case of a density transition, hence the name Transition Radiation, but for astrophysical plasmas, where such density transitions would be smoothed out by motions of the hot particles, it is more appropriate to consider the case of density fluctuations.In the case of such density fluctuations, perhaps due to wave turbulence in the plasma, it was first shown that the intensity of the radiation is very small and perhaps undetectable, for a reasonable level of turbulence. But recently Platinov and Fleishman have considered the case of emission near the plasma frequency. They found that there is a large enhancement of the emission due to the plasma frequency resonance, and so they gave emission in this regime the name Resonant Transition Radiation. We might expect an effect near the plasma frequency because the group speed of electromagnetic waves in a plasma approaches zero as the frequency of the waves approaches the plasma frequency.
The discussion so far as been about incoherent emission, in which electrons act separately to produce their emission. In this case, n particles produce n times the emission of one particle, and the photons emitted have no coherence--that is, no phase relationship. In this case the brightness temperature is related to the effective energy of the individual particles--the actual temperature in the case of a thermal distribution of particles, or the kinetic temperature for a non-thermal distribution.It is also possible for electrons to act together to produce electromagnetic radiation, in which case the electrons all undergo acceleration in phase, acting together to produce photons that are in phase. In this case, the brightness temperature can far exceed the actual temperature or kinetic temperature of the electrons. In the case of the Sun, coherent bursts can reach brightness temperatures of 1015 K!
Formally, absorption of radiation is expressed as an imaginary part of the wave frequency, i.e. a purely oscillating wave has the form
E = Eo ei(kx-w t) while a damped wave has the formE = Eo ei[kx- (w + ig)t] = Eo ei(kx-w t) e-gt. where g is the damping rate. (Note that this can be converted to an equivalent absorption coefficient, k, or emissivity loss per unit distance, by multiplying by the wave speed, g = k w/k.)Under some circumstances, the damping rate can be negative, so that we have negative damping (or negative absorption), i.e. wave growth. In this case, g is called the growth rate. Typically, different coherent mechanisms will produce this kind of linear growth over 3 or 4 e-folding times, and then the linear growth will saturate due to some non-linearity, such as running out of energy available for growth.
Plasma Emission
An ionized gas, i.e. a plasma, can support a wide range of wave modes. One mode, called a Langmuir wave, is so ubiquitous that it is called by the generic name plasma wave, or plasma oscillation, and the associated electromagnetic emission that it can produce is called plasma emission. The plasma frequency has a particularly simple form that depends only on the electron density:np = wp/2p = (1/2p)[4pnee2/me]1/2 ~ 9 x 103 ne1/2 ,where the units are cgs units, and so the electron density is expressed in units of cm-3. This is the natural frequency of oscillation of a plasma, so any disturbance that provides energy to the plasma is likely to generate Langmuir waves at this frequency. Note that Langmuir waves themselves are longitudinal electrostatic waves, and are not observable from outside the plasma. However, under certain circumstances they can excite transverse (electromagnetic) waves at the same frequency that can escape.As an important example, imagine a distribution of fast electrons in the so-called bump-on-tail distribution, as shown schematically below:
Here the electrons are said to form a beam, where the electrons stream along the magnetic field. The positive slope on the energy distribution is a source of free energy, and plasma waves can grow at the expense of the electron energies. These plasma waves can then scatter off ions (or couple to low-frequency ion-acoustic waves), to generate radio waves at the plasma frequency: wl + wi = wp. In addition, two plasma waves going in nearly opposite directions can interact to produce radio waves at twice the plasma frequency: wl + wl = 2wp. This is called "2nd-harmonic" emission, and is an example of the wave-wave interactions mentioned at the beginning of this lecture. Here is an example of radio emission produced by an electron beam traveling outward in the solar corona: As the electrons stream outward, the electron density in the corona falls greatly, and the corresponding radio frequency of the emission goes to lower frequency. If we know the speed of the electron beam, we can deduce the density in the corona and interplanetary space. Conversely, if we know the radial density profile we can deduce the speed of the electrons. It is very important to understand that the intensity of the emission is only a function of the number of e-folding times over which growth occurs, and is not a diagnostic of the electron energies or other parameters of the source. This is a general property of coherent emission--intensities do not provide a useful diagnostic (at least not that we know how to interpret). Electron-Cyclotron Maser (ECM) Emission
Like plasma emission, this mechanism uses a source of free-energy in the particle distribution to provide energy for wave growth, but this time the waves that develop may already be in the form of electromagnetic radiation. In this case, the source of free energy is not in the energy dependence of the particle distribution, but rather in the angular dependence, or pitch-angle distribution. The relevant geometry is downward-going electrons in a converging magnetic field. In this situation, electrons with a sufficiently large pitch angle will mirror, or reflect, but electrons with a smaller pitch angle can escape. The pitch angles smaller than the limit between mirrored and escaping particles are said to be in the loss-cone. The loss of particles in this cone sets up a pitch-angle anisotropy, and under certain conditions the same electron-cyclotron (gyroresonance) waves that we met earlier, with frequencyw - kv|| = sWBsee a distribution with a positive slope in their inertial frame. In the equation above, the gyrofrequency is WB = eB/mec, as before, but now we explicitly include a term kv||, which represents the doppler shift of waves of wavenumber k seen by particles moving at speed v||. Note that there is no positive slope in energy in the "rest" frame of the distribution, but there is for the wave frame. The result is that huge amounts of energy are available to go into production of radio waves near harmonics of the gyrofrequency. ECM emission is thought to be responsible for bursts seen in the outer atmosphere of Earth, called kilometric radiation, and in Jupiter's magnetosphere. It is also responsible for extremely bright, narrowband bursts from the Sun and stars, called spike bursts. The largest solar radio burst ever recorded, on 2006 Dec 06, was due to millions of individual spikes of this coherent mechanism. Below are some plots of the data from this event.
This shows two levels of zoom into the high frequency and time resolution data. The upper (red) plot shows individual spike bursts for about 2 seconds near the end of the event. The lower (blue) plot shows the full 1 us time resolution for the region in the vertical white lines of the upper plot. Notice that the spikes are narrow band (about 3-5 MHz wide) and come and go on a timescale shorter than 20 ms.