Introduction

We have seen what the receivers and front end (feed, amplifier, mixer) must do to sensitively detect weak radio emission.  We have also looked at the way interferometry can be used to image the sky, and how pairs of antennas (baselines) measure Fourier components of the sky brightness distribution.  We now will go back and look at what special aspects of the receiving system are needed to do interferometry.

The first part of the receiver is the heterodyning to bring the RF (radio frequency) down to a manageable intermediate frequency (IF) that we can work with.  This requires a mixer and local oscillator (frequency reference), as shown in Figure 1, below:
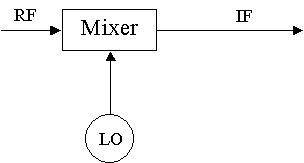
Figure 1: Heterodyne receiver, which uses a local oscillator (LO)
operating at frequency wo, to tune to the desired radio frequency (RF)
and mix with RF at a wide band of frequencies, and strip off a lower
bandwidth section of intermediate frequency (IF) for further processing.

For interferometry, we must correlate the signals from two antennas, which requires a number of additional considerations.  The main one is to ensure that the receivers of the two antennas are operating at exactly the same frequency.  If one were on a frequency different by only 1 Hz, the resultant phase between the two would change by 360 degrees every second!  In the past, it was not possible to transmit a broadband signal from each antenna, which meant that the signal at each antenna had to be mixed down to a lower frequency. That required the use of a reference signal sent to each antenna. Figure 2 shows an example of such a scheme. To control the frequency, a phase lock system was used as in Figure 2.

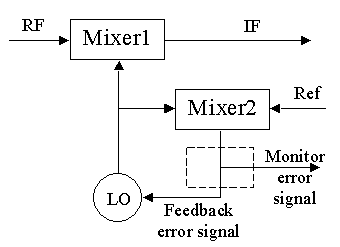
Figure 2: Adding a phase lock loop, which compares the LO output
with an external reference frequency and sends an error signal back
to the LO to keep it in perfect phase lock with the reference signal.
Each antenna receives the Ref signal from the same source, so all
receivers are locked to the same frequency.

Mixer 2 compares the LO to a frequency reference, which comes from the same frequency source for all antennas.  Any error in the phase results in an error signal that is fed back to the oscillator to adjust its frequency to maintain exact frequency tuning.

With modern technology, it is now possible to transmit broadband signals via optical fiber. The EOVSA system, for example, transmits two 1-18 GHz RF signals multiplexed onto a single optical fiber to the central control room. In the confined space of the control room, it is possible to distribute the local oscillator signals directly to the 15 downconverter modules and avoid the need for a distributed phase lock system.

Let's look at what happens to the signal after it leaves the EOVSA front end and enters the receiver.  The figure below is the block diagram for a downconverter module in the Expanded Owens Valley Solar Array.

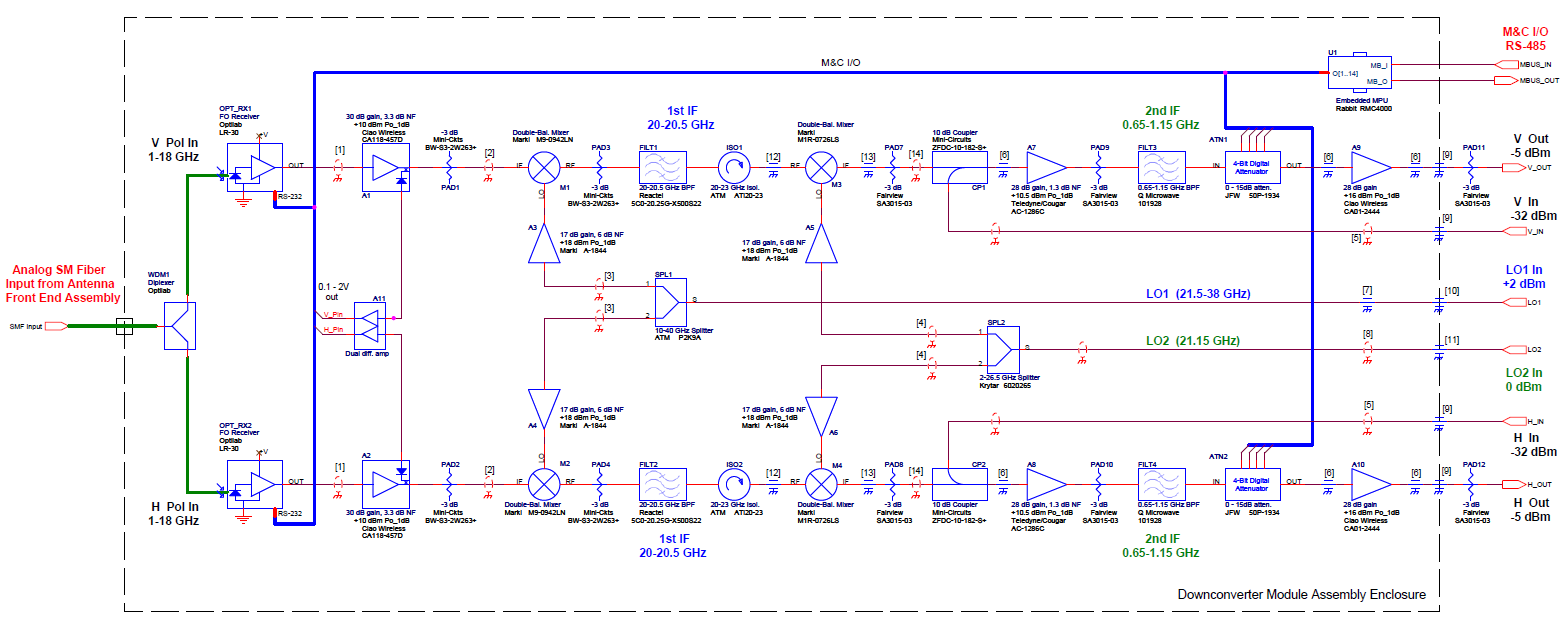
This is a dual-channel receiver, with H pol and V pol signals being received separately on optical fiber. The signals enter on the left and exit on the right. The signals are converted to electrical form, go through two stages of frequency conversion, which selects a 400 MHz intermediate frequency (IF) portion of the incoming 1-18 GHz radio frequency (RF), adjusts its power level by means of amplifiers and attenuators, and then provides this clean 400 MHz IF to the digitizers in the correlator chassis (not shown). Click this link for a description of the EOVSA downconversion and frequency tuning.

The IF signal from each receiver looks like a noise signal.  Part of the waveform is really signal from the source, and part of it (perhaps the largest part) is noise.  If both signal and noise look the same, how do we tell the difference?  The essential point is that source signal will be correlated between the two antennas, while the (locally generated) noise signal will not.  This is illustrated with the simulated waveforms from two antennas, below:
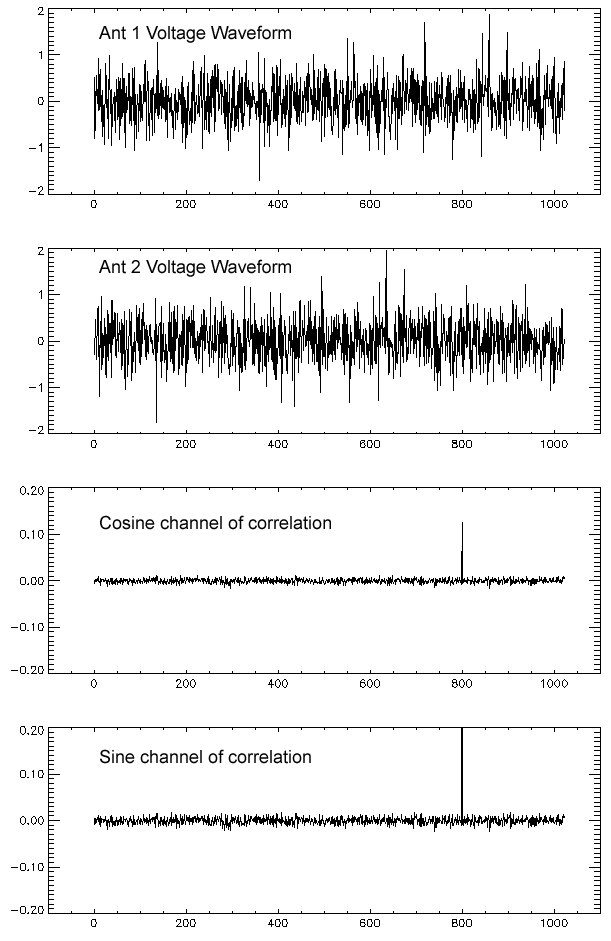
Figure 3: Two simulated voltage waveforms, with phase 30 degrees, with the
waveform for antenna 1 shifted by 800 time samples.  The noise level is 1/5 of
the signal level in this example.  The waveforms appear to have no relation to
one another, but when correlated they give the plot in the third panel (cosine
channel), which shows a good correlation (spike) at a time lag of 800 samples.
Shifting the antenna 1 waveform by 90 degrees and performing the correlation
again gives the result shown in the bottom panel (sine channel).  The combination
of the sine and cosine channels gives an amplitude of 0.268 and phase of
30.2 degrees.  The correct values are 0.25 and 30 degrees.

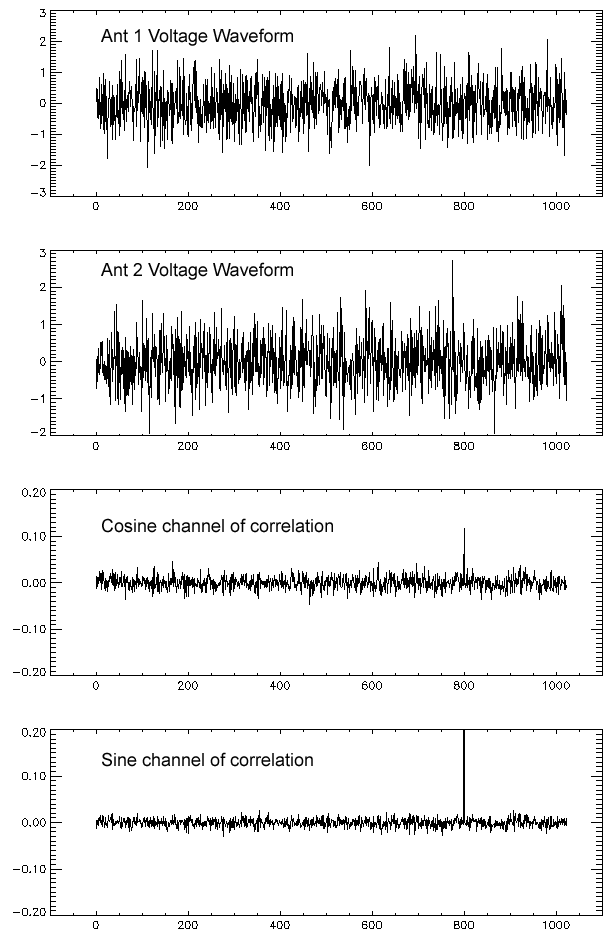
Figure 4: Two simulated voltage waveforms, with the same characteristics as for
Figure 3, but now the noise level 5 times higher and is now equal to the signal level.
Because the noise is uncorrelated, the correlated signal is hardly affected, and gives
and amplitude of 0.245 and phase of 30.83 degrees, compared to the correct
values of 0.25 and 30 degrees.

Given time varying voltages V₁ and V₂, the correlation is found by multiplying them, with one delayed by the geometrical delay t_g= B . s/c, then averaging, i.e.

r = <V₁(t)V₂(t)>

where < > denotes the expectation value, found by averaging over some integration time.  Considering for the moment a monochromatic time-varying signal

V₁(t) = v₁ cos[2πν(t−τ_g)]
V₂(t) = v₂ cos[2πνt]

we have

r = <v₁v₂ cos[2πν(t−τ_g)] cos[2πνt]>
   = v₁v₂ <cos²(2πνt) cos(2πντ_g) + cos(2πνt) sin(2πνt) sin(2πντ_g)>
   = v₁v₂ cos(2πντ_g)

Since the geometrical delay τ_g changes due to the Earth's rotation, the relatively slowly varying cosine term causes the oscillations that represent the motion of the source through the interferometer fringe pattern.  In the old days of chart recorders, this fringe pattern was traced on paper and its amplitude and phase could be measured by hand.  The rate of fringe oscillations is called the natural fringe rate.  The fringe frequency is

ν_F = dw/dt = −Ω_e u cos δ

where Ω_e is the Earth rotation rate, w = (B_λ . s) is the spatial frequency corresponding to the projected baseline z-component given by the coordinate transformation from the previous lecture, u is the usual E, or y-component spatial frequency, and δ is the declination of the phase center.  The geometry is as shown in Figure 5.

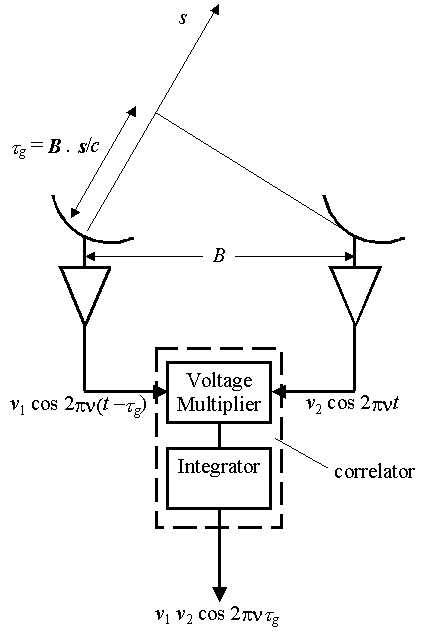
Figure 5: The geometry and block diagram leading to the measured cosine component
of the correlation.  Both the multiplier and the integrator are part of the device called the
correlator.  A refinement is shown in Figure 6.

A major refinement is to use a second correlator, and shift one of the signals by π/2, so that both sine and cosine components are measured simultaneously, as shown below.  The components in the dashed box in Figure 5 are indicated by each circled X in Figure 6.

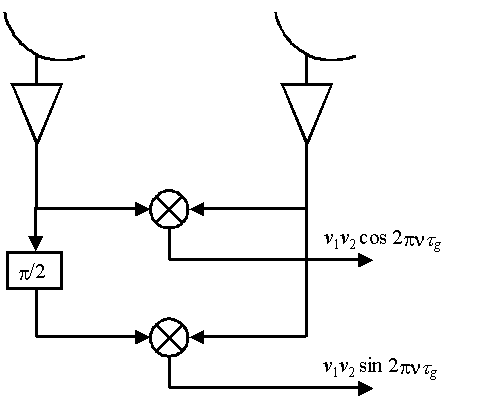
Figure 6: Inserting a phase shift of π/2 in one of the antennas and doing a
second correlation allows both sine and cosine components to be measured
simultaneously.  These are recorded and become the complex visibility at
spatial frequency u,v corresponding to the projected baseline between the
antennas.

The quantities measured out of the correlator are the real and imaginary parts of the complex visibility measured with the baseline, whose normalization is obtained by the calibration procedure, which we have not yet discussed.  You may wonder how we accomplish the 90 degree phase shift over a finite IF bandwidth Δν.  This was done in the old OVSA receivers by changing the phase of the reference signal used to phase lock the local oscillator.  Note that this is not equivalent to a time delay, which would shift the phase by different amounts for different frequencies, but rather it shifts the phase of each frequency separately.  In the new EOVSA system, we use the digital correlator to do the phase shifting.  As it turns out, phase shifting, or synchronous detection, is also important for eliminating any DC offsets.  If we multiply two waveforms with a DC offset, the offsets will give a non-zero signal even when there is no correlation in the signals.  This is eliminated by periodically inverting the signal at the antenna, and then synchronously inverting the signal again at the correlator.  In this way, the signals stay correlated while any unwanted DC offset gets inverted periodically and averages to zero.

To discuss correlators further, we will use the NRAO Summer School lecture on cross correlators.