Introduction

We have discussed how an interferometer array measures the complex visibilities of the source.  This is a good opportunity for a review of that relationship.  The basic need for calibration is to correct the measured visibilities V'(u,v) to approximate as closely as possible the true visibilities V(u,v).

The basic equation for a synthesis array is
 

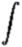V(u,v) =		A(l,m) I(l,m) exp[−i2πul + vm)]	dl	dm .         (1)

where (l,m) are the direction cosines with respect to the phase center,
           (u,v) are the projected baseline coordinates in wavelengths, u = B_l,λ, v = B_m,λ,
           V(u,v) is the true visibility evaluated at u, v,
          A(l,m) is the normalized primary beam pattern (beam of a single antenna)
            I(l,m) is the brightness distribution of the source

Recall that the exponent comes from B_λ. s = ul + vm + wn = ul + vm + τ_gν, so when we say "with respect to the phase center," we mean that the group delay is compensated so that τ_gν  = 0.

We can rewrite this to emphasize the discrete sampling with antenna pair i,j at times t by

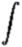Vij(t) =		A(l,m) I(l,m) exp[−i2πuij(t)l + vij(t)m)]	dl	dm .         (2)

The term ul + vm is the geometric phase difference Δφ, produced by the geometric path length difference between antenna i and antenna j from the part of the source at location (l,m) relative to the phase center.

Recall that

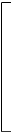u

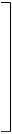1

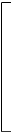sin ho

cos ho

0

..

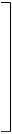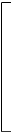Bx

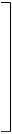Bλ. s =

v

=

−sin δo cos ho

sin δo sin ho

cos δo

By

w

λ

cos δo cos ho

−cos δo sin ho

sin δo

Bz

where the hour angle and declination (source coordinates) are h_o, δ_o, and the baseline lengths are B_x, B_y, B_z.  Then the geometric phase difference at the phase center (the w term, at l = m = 0) is

φ_g = 2πτ_gν  = (2π / λ)[B_xcos δ_o cos h_o − B_ycos δ_o sin h_o + B_zsin δ_o].

We can see what can affect the geometric phase by taking the differential of this expression:

dφ_g = 2πνdτ_g  = (2π / λ)[dB_xcos δ_o cos h_o − dB_ycos δ_o sin h_o + dB_zsin δ_o
                                  + dα_ocos δ_o (B_xsin h_o + B_ycos h_o)
                                    + dδ_o (−B_xcos h_o sin δ_o + B_ysin h_o sin δ_o + B_zcos δ_o)],           (3)

where we have used the relation between right ascension and hour angle: h_o = LST − α_o, so dh_o = −dα_o.  Equation (3) shows how baseline errors (dB_x, dB_y, dB_z) and source position errors (dα_o, dδ_o) will affect the error in group delay dτ_g (or yield an error in phase dφ_g).  Note that a clock error is equivalent to a source position error dα_o.

If we have a source whose position is known, we can use equation (3) to find the location of the antennas (this is called baseline determination).  The error in antenna position is largely independent of the baseline lengths.  For example, say that we can measure dφ_g to within 1^o at 5 GHz (λ = 6 cm).  Then we can measure dB_x, dB_yand dB_z to a precision of order

(1 / 360) 6 cm ~ 1 / 60 cm

even though B = (B_x² + B_y² + B_z²)^1/2 = 5000 km or more (VLBI).

This has been used to verify and accurately measure motion of the Earth's crust due to plate tectonics.

Alternatively, once the baselines are accurately known, we can observe unknown sources and find their positions, (α_o, δ_o), to high accuracy.  This does require long baselines, because to minimize (dα_o, dδ_o) we have to have large (B_x, B_y, B_z).  So once again, VLBI is needed.  Determining accurate source positions is called astrometry, and VLBI is the most accurate method for establishing a highly accurate coordinate system for the sky, of order 1 milliarcsecond in absolute position.

A properly designed synthesis array will preserve a linear relationship between the measured visibilities  V'(u,v) and the actual visibilities V(u,v), which in general can be written

V_ij(t) = G_ij(t)V_ij(t) + ε_ij(t) + η_ij(t)         (4)

where we have broken the constant term into an offset ε_ij(t) and a stochastic noise term η_ij(t).  The proportionality factor G_ij(t) is called the complex gain for the ij-th baseline.  All of the terms in this equation are "complex," but this is really just a convenient way of using one equation to represent the two outputs of each correlator -- the cosine and sine components (or real and imaginary).

The meaning of the complex gains can be seen by expressing them in terms of gains of individual antennas:

G_ij(t) = g_i(t) g_j^*(t) = a_i(t) a_j(t) exp[i(φ_i(t)−φ_j(t))]         (5)

where a_i(t) is the multiplicative gain of the i-th antenna, and φ_i(t) is the phase of the i-th antenna. When the array is optimized, these numbers can be determined by measuring a point source at the phase center.  Since the expected amplitude of such a source is constant, and the expected phase is zero, any differences in the a_i and any non-zero phase differences φ_i − φ_j must be due to the antennas themselves.  Note that for N antennas, we measure G_ij on N (N − 1)/2 baselines, so for large N the problem is well over-determined.  In this case we can use a least squares algorithm to solve for the antenna-based complex gains g_i, i = 1, 2, ... N.

However, first the array must be optimized, which requires some initial calibrations:

Antenna Pointing and Gain
Our equation for inverting the visibilities assumes that the normalized antenna primary beam distribution A(l,m) is independent of time and identical for each antenna.  The antenna tracking center must follow the same intended position for all antennas (generally the same position as the phase tracking center, although this is not essential).  Errors in tracking can cause reduced sensitivity and distortions in extended objects.  For point sources, the tracking accuracy should be better than 0.1θ_FWHM, where θ_FWHM = angular size of FWHM of the primary beam.  For extended objects (e.g. the Sun) that cover a large part of the primary beam, the pointing accuracy should be even better, say θ_FWHM/20.  For OVSA at, say, 10 GHz, where the 27 m primary beam is 4.6 arcmin, this would require about 14" accuracy.  For the 2 m antennas, the requirement is relaxed to about 3 arcmin.

The antenna pointing error is the difference between the actual pointing position and the desired one, and it has a complicated directional dependence due to

• misalignment of antenna rotation axes
• gravitational deformation (sagging)
• non-perpendicular axes
• atmospheric refraction
• differential heating of the structure
• wind loading

Often, rather than trying to describe axis and deformation errors based on engineering of the structure, an ad-hoc trigonometric dependence on the sky is determined using multiple measurements of sources around the sky.  For the OVSA 27 m antennas, we point one antenna at the source and move the other in a prescribed pattern. (J069 arcfile)

For the OVSA 2 m antennas, which are not sensitive enough for this, we use the solar disk (which is nearly a point source for the 2 m primary beam).  One problem is that this gives only a single declination track over a day, so it is not possible to optimize for pointing over the entire sky. (J067 arcfile)

Delay Calibration
We have already discussed delay calibration in some detail in Lecture 8, as well as the related ideas of bandpass calibration.  Recall that an error in delay of only a few nanoseconds will cause the different parts of the observing band to partially interfere (different frequencies in the band arrive with different phase), leading to a drop in the amplitude.  Obviously, we need to have the delays optimized.

Time and Place
The time of day and location of the antennas must be known to relatively high accuracy -- needed for determining the geometric delay.  A clock error of 1 s, or a baseline error of a few cm, will cause a serious phase shift of the source over, say, 10 minutes.  At OVRO, using a GPS clock and measuring baselines with cosmic source calibration (we will discuss this shortly), we get a time accuracy of << 1 ms, and baseline errors of about 3 mm.  Therefore, these effects are not serious over a short time interval, but may still be problematic over 8 hours.  This is one reason that we do phase calibration observations every ~ 2 hours.

Routine Corrections
Several additional corrections must be done, generally by the "on-line" computer in real time.  These are:

1. System optimization
1. level control, or gain control -- for VLA, this is done using an ALC (automatic leveling control) loop to keep the threshhold optimum on the digital correlator.  At OVRO, descrete attenuation is switched in as necessary to avoid saturation (and non-linearity).
2. Round trip phase measurement (to stabilize for phase changes due to temperature effects in the LO reference frequency).
3. Pointing control (adjusting the antenna pointing according to the pointing parameters).
2. Timing corrections and calibrator fluxes
1. The Earth does not rotate uniformly, due to wind, tide, and other global effects, precession and nutation.  These parameters are available in terms of timing corrections from government sources.
2. The fluxes of calibrators can change and must be monitored by specially designed radio telescopes for absolute flux calibration.  We will see more about this shortly.
3. Path length changes due to the troposphere and ionosphere.
1. The refractive index of the atmosphere differs from unity by about 1 part in 3000, so there is an additional delay in traversing the atmosphere of about 8 ns, or an "extra path length" of about 23 m at the zenith.  This would not matter for a plane parallel atmosphere in which the antennas are alll at ground level, since only the relative phase matters.  However, if we refer the phase to a calibrator at some other sky location (different zenith angle) we have to take account of the extra path length.
ΔL = (Δh + cτ_gL sec z / r_o) sec z
where z is the zenith angle, L = 0.228 P_tot + 6.3 w is the zenith path length due to the atmosphere, P_tot is the total pressure at ground level, w is the vertical column water vapor content (cm), r_o is the Earth radius, and Δh is the height difference of the antennas.  The second term is small, ~ 10⁻⁵ of baseline length, except for large z.  The wet component is generally a small fraction of the dry component, but it is also variable over the sky, so Δφ is in fact dominated by the wet component.
2. The ionosphere causes a frequency-dependent refraction that is proportional to λ², so is worse at low frequencies.  The "extra" path length is
L_i = −40 ν ⁻² N_e
and is negative because the index of refraction n < 1 in an ionized medium.  N_e is the electron column density in units of 10¹⁸m⁻² (typically near unity for Earth's ionosphere).  The differential path length is then
ΔL_i = cτ_gL_i / (r_o cos²z + 2H)
where H is the height of the ionosphere (about 600 km).
4. Absorption by troposphere and ionosphere
1. In addition to refraction, the atmosphere also absorbs radiation, which has two effects: reduces flux by S = S_o exp(−τ>_a sec z), increases noise (atmospheric emission) by T_atm [1 − exp(−τ_a sec z)]

where τ_a = α₀ + α₁P_v = atmospheric opacity and P_v = partial pressure of water vapor in millibars.  τ_a can be measured using "tipping radiometers" which measure the sky brightness as a function of zenith angle.  The water vapor line near 22 GHz is a favorite part of the spectrum to use for this purpose.

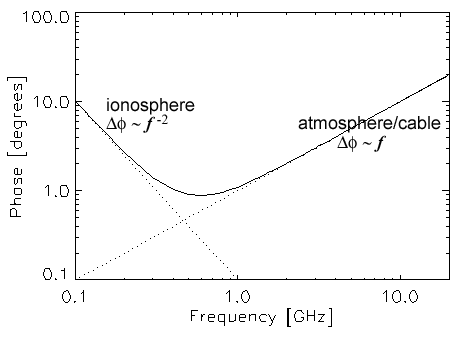
Figure 1: The dependence of phase errors due to the ionosphere and troposphere
as a function of frequency.  Phase errors as small as about 1 degree near 1 GHz
can rise to 10-20 degrees at both high (20 GHz) and low (100 MHz) frequencies.
The phase errors can be much greater than this under certain conditions.

The Offset and Noise Terms
Before getting to the final calibration, it is worthwhile to look at the unwanted offset and noise terms in equation (4).  The offset term, ε_ij(t), is generally kept small by design, and the amplitude part can be measured and subtracted by attenuating the signal.  This is analogous to "dark current."  The phase part is generally not a problem, since offsets on two antennas should not be correlated and it can be reduced to zero by using phase switching in the receiver.

The noise term, η_ij(t), is part of the system and generally vastly outweighs the signal, as we discussed in Lecture 5.  But it can be reduced by averaging over some length of time.  As we saw when discussing sensitivity, the noise is proportional to sqrt(t), where t is the integration time.  Over this same period, the signal remains constant, so S/N increases.

An interesting question is, what kind of average should we perform?  Often the data are represented as amplitude and phase, and one can either average amplitude and phase separately, or average as a vector average.  A vector average may seem the best choice, but in many (most) cases the phase variations are uncorrelated with the amplitude variations (e.g. due to weather, temperature, or cable length changes).  In this case, it is better to average amplitudes separately, and fit for any phase wind before determining phase).

Final Astrometric Calibration
We are fortunate that there are many point-like radio sources scattered around the sky and relatively well isolated from other confusing sources.  When we measure such sources with an interferometer array, we can use the known visibilities (constant amplitude and zero phase) to calibrate the system.  This is particularly useful because the signals traverse the entire system, including the ionosphere, troposphere, etc.  It is not perfect, however, because generally the calibrator sources are in different sky locations than the source of interest -- unless the source of interest is strong enough for self calibration.  We will discuss this in a moment.

As an example, let us take a look at the VLA calibrator manual.  As you can see, there are lots of point sources, but they may not be point sources at all frequencies and size scales.  Therefore, there are restrictions of baseline length (u,v spacing) and frequency.  Note again that these sources can be variable.

Baseline-based Vs. Antenna-based Calibration
After suitable averaging, we are left with (for a point source)

G_ij(t) =  V_ij(t)/S         S = flux of the point source

where G_ij is the baseline-based gain (complex -- includes both amplitude and phase components).  For a sufficient number of antennas, however, these are not all independent and we can do better.  Let us write the baseline gain factor as

G_ij(t) = g_i(t)g_j^*(t) g_ij(t)

where the last term is a residual term very close to unity that basically keeps track of errors (usually < 1%).  These complex numbers can be separated into amplitude and phase:

A_ij(t) = a_i(t)a_j(t) a_ij(t)
Φ_ij(t) = φ_i(t) − φ_j(t) + φ_ij(t).

Let us write V_ij(t) = a_ij(t) exp[iφ_ij(t)] ;  V_ij(t) = A_ij(t) exp[iφ_ij(t)] . Then for a point source the measured amplitudes and phases are

A_ij(t) = a_i(t)a_j(t) a_ij(t) S
Φ_ij(t) = φ_i(t) − φ_j(t) + φ_ij(t)

which can be solved for a_i and φ_i for all N antennas, provided g_ij is close to unity, using a least squares method (using logarithms for the amplitude terms).  The error terms can then be checked to show if there are any problems.  The errors are acceptable when

φ_ij(t) = Φ_ij(t) − φ_i(t) − φ_j(t)  < 1^o
a_ij(t) = A_ij(t) / [a_i(t)a_j(t) S]  within 1% of 1.00.

One advantage of antenna-based solutions is that they can be obtained even without all of the baselines.  This is especially important for partially resolved or confused calibrators, as we saw with the restrictions in the VLA calibrator list.  In this case one simply applies the solution on baselines that meet the criteria so that the source is a good point source.  Note that this approach uses the fact that we have observed a point source calibrator.  In fact, one can also do this on a more complicated source, as we will now describe in the context of Selfcal (self calibration).

For our discussion of self calibration, we will use Tim Cornwell's NRAO Summer School lecture notes.