Phys 728, Spring 2003
Homework Problem Set #4
4.1. Construct an array f(u,v) of 1024 x 1024 pixels
representing a circular aperture of 10 m diameter, operating at 3.6 GHz,
with each pixel corresponding to 1 l. How many pixels in diameter
will the aperture be? Obtain the primary beam F(l,m)
by taking its Fourier Transform using IDL or other package of your choice.
Print an image of the normalized power pattern |F(l,m)F*(l,m)|,
shifted appropriately. Also plot the 1-d power profile through the
center of the power pattern, labeling the horizontal axis in arcminutes.
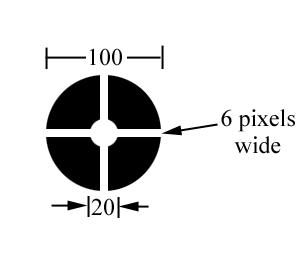
4.2. Construct the aperture below by starting with a 100 pixel
diameter circle, cutting out a circular hole of 20 pixel diameter and a
cross of width 6 pixels, and obtain the primary beams F(l,m)
for both the blocked and unblocked apertures. Show that the ratio
of peak of the power patterns of the blocked to unblocked aperature (i.e.
|F(0,0)F*(0,0)|blocked / |F(0,0)F*(0,0)|unblocked)
is the same as the efficiency, given by expression hbl
= (1- area blocked / total area)2.