Go to EE494 Index Experiment | 1 | 2 | 3 | ECE Lab Home
![]()
|
Go to EE494 Index Experiment | 1 | 2 | 3 | ECE Lab Home |
|
| EE 494 |
| Electrical Engineering Laboratory IV (Part B) |
| Version 1.3 |
| TUTORIAL: Introduction to Filter Design |
1.1 Objectives
1.2 Equipment Needed
1.3 References
1.4 Background
1.5 Specifying Butterworth Filters
1.6 Specifying Chebyshev Filters
1.7 Conversion of Specifications
1.8 Examples of Filter Realizations
1.9 Student’s Filter Specification
In this experiment the student will become familiar with methods used to go from a filter specification to specifying the polynomial transfer function of the filter. Then the student will learn to translate the polynomial transfer function into a working filter design.
A decent scientific calculator.
A few µA741 integrated circuit operational amplifiers, resistors and capacitors and a prototyping board.
S. Franco, Design with Operational Amplifiers and Analog Integrated Circuits, McGraw-Hill Inc., 1988.
M. E. Van Valkenburg, Analog Filter Design, HRW, 1982.
A. B. Williams, Electronic Filter Design Handbook, McGraw-Hill Inc., 1988.
 |
|
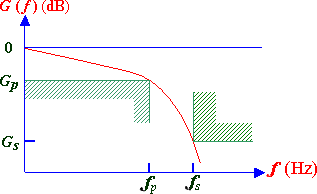
Figure 1.1: A filter specification diagram with a sketch of a Butterworth response that exactly satisfies the specs. |
The assignment of designing and building analog filters can be broken up into various tasks. We will assume that the given filter specification is presented in the form shown in figure 1.1. The interpretation of the diagram is the following:
It is desired to build a low pass filter whose passband lies in the region 0 ≤ f ≤ f p. The transfer function | G( f ) | is almost invariably given in units of dB.
Within the passband, the magnitude of the transfer function may vary between zero and Gp.
When it enters the stop band, the magnitude of the transfer function should decrease to Gs or less as the frequency fs is reached.
A possible transfer function, in the form of the smooth curve, is shown in figure 1.1. We plan on realizing the filter using a linear analog-circuit. Such circuits have transfer functions whose magnitude squared is an even polynomial in the frequency variable f. Therefore the first step in the design process is to find a polynomial transfer-function that will satisfy the specifications. Many different well-known polynomial transfer-functions are used for approximating filter specifications. Because of time constraints, however, our attention will be confined entirely to Butterworth and Chebyshev polynomial realizations. They have the advantage of having over the years acquired extensive tabulations. But it must be understood at the outset that additional polynomial realizations exist, and that with each is associated a set of advantages and disadvantages which are discussed in the literature.
We will now address the question of how to fulfill the specification of the filter by using Butterworth and Chebyshev transfer functions.
1.5 Specifying Butterworth Filters
At the outset we observe that Butterworth filters have the magnitude characteristic given by
where n is the order of the filter and fc is the frequency at which the transfer function magnitude is reduced by 3 dB. This class of filters has a monotonically decreasing amplitude characteristic. It has no ripples in the passband, in contrast to Chebyshev and some other filters, and is consequently described as maximally flat.
In order to fully specify the filter we need an expression for determining n as well as a method for computing the fc needed in (1.1). To reach this goal we substitute the filter specifications at fp and fs into (1.1) to obtain
1 + ( fp / fc )2n = 10 -(Gp / 10)
(1.2)
1 + ( fs / fc )2n = 10 -(Gs / 10)
(1.3)
From the last two equations we readily get the two expressions
Taking the ratio of the last two expressions we readily find that
(1.6)
The example which follows will illustrate the use of the above equations.
Example 1: We wish to design a Butterworth filter satisfying Gp = -1 dB at fp = 3 kHz and Gs = - 25 dB at fs = 8 kHz.
Substituting the specifications given into (1.6), we obtain the solution
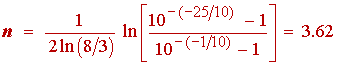
(1.7)
We need an integer exceeding that given in (1.7), so we fix the value of n at 4. We now simply need to find the value of fc needed to finish specifying ( 1.1 ). Since n = 4 exceeds the value of n found in (1.7) we will have some extra latitude in choosing fc. To find fc we substitute n = 4 into (1.4) and (1.5) to obtain the two equations
(1.8)
(1.9)
The last two equations produce the two results for fc,
fc1 = 3.55 kHz
(1.10)
fc2 = 3.90 kHz
(1.11)
If we choose a value of fc somewhere in the range fc1 < fc < fc2 then the design will have some tolerance in the passband as well as in the stopband.
We use the geometric mean
(1.12)
With n fixed at 4 and fc fixed at 3.7 kHz, we reevaluate (1.1) at fp and fs to find
G ( fp ) = - 0.744 dB
(1.13)
G ( fs ) = - 26.8 dB
(1.14)
Comparing the above results to the original specification we find that the specifications are exceeded. We therefore have some latitude in our design to compensate for tolerances of component values.
1.6 Specifying Chebyshev Filters
 |
|
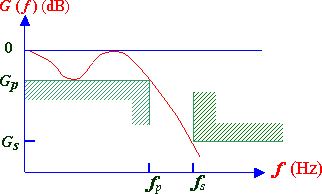
Figure 1.2: A filter specification diagram with a sketch of a Chebyshev response that exactly satisfies the specs. |
The filter specifications, as well as a sketch of a Chebyshev filter response, are shown in figure 1.2. As can be seen in the diagram, this class of filters has an amplitude characteristic which has ripple in the passband, in contrast to the maximally flat Butterworth filters. The end of the passband, the frequency fp, is also the cutoff frequency fc appearing in the equations which are presented below.
Chebyshev filters have an amplitude characteristic given by
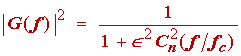
(1.15)
The functions C n( · ) are Chebyshev polynomials. They also have the nonpolynomial forms, given below, which are very convenient for hand calculation. As can be seen from the following equations, there is one form for the passband and one form for the stopband.
Cn( f / fc ) = cos [n cos-1( f / f c)] , for | f / f c | ≤ 1 (1.16)
Cn( f / f c ) = cosh [n cosh-1( f / f c)] , for | f / f c | ł 1 (1.17)
Examination of (1.16) shows that in the passband the Chebyshev polynomials take on values between -1 and 1. As a consequence we conclude from (1.15) that in the passband
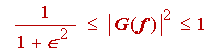
(1.18)
The above is the magnitude of the ripple in the passband. The upper bound corresponds to 0 dB. The lower bound corresponds to GpdB. From this we obtain the expression for Î2, in terms of the ripple specification Gp, in the form
Î2 = 10 - (Gp / 10) - 1
(1.19)
If we could obtain an expression for calculating the value of n needed in (1.15), we would be in a position to fully specify the Chebyshev filter. To attain this objective we substitute the filter specifications at fs and fp (using fp for fc ), as well as (1.19) into (1.15) to obtain
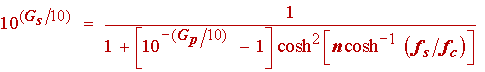
(1.20)
Solving for n in the above we obtain
(1.21
An example will be used to demonstrate the application of the theory.
Example 2: We wish to design a Chebyshev filter satisfying the same specifications as in the previous example, namely Gp = -1 dB at fp = 3 kHz and Gs = -25 dB at fp= 8 kHz.
Substituting the specifications given into (1.21), we obtain for n
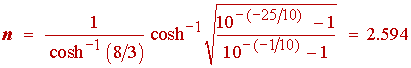
(1.22)
Since n has to be an integer exceeding that given in (1.22), we fix the value of n at 3. Since n = 3 exceeds the value of n found in (1.22), we can use the extra freedom to provide some tolerance margin by exceeding specifications. We can either increase fc or decrease the ripple in the passband.
We choose, quite arbitrarily, to decrease the ripple in the passband to 0.5 dB which means that now Gp= 0.5 dB. Substituting this into (1.19), we obtain
Î2 = 10 - (- 0.5 / 10) - 1 = 0.1220
(1.23)
When this value of Î2 is substituted into (1.15) and that in turn is evaluated at the stopband frequency of 8 kHz, we find that
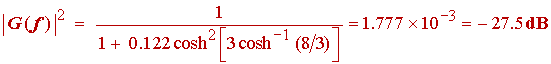
(1.24)
Comparing the above results to the original specification we find that the specification at the edge of the passband is better by 0.5 dB and that the specification in the stop band is improved by 2.5 dB. This design therefore has some compensation for variations due to temperature and to tolerances of component values.
We have demonstrated how to determine the specifications for Butterworth and Chebyshev filters. It is seen that Chebyshev filters have the advantage that a lower order polynomial will satisfy the specifications as compared to Butterworth filters. But on the other hand Butterworth filters have a more linear phase-characteristic than do Chebyshev filters, and this may affect the choice of design for specific cases.
1.7 Conversion of Specifications
In the previous section we have shown how to specify the polynomial form of the magnitude-squared transfer-function | G ( f ) |2 . This is in all cases an even polynomial in the frequency variable f . Some additional work is required before we arrive at a factored form for the transfer function G ( s ).
The steps required involve replacing j2p f with the Laplace transform variable s in equations (1.1) and (1.15), which is equivalent to replacing f 2 with -( s / 2p )2 to obtain | G ( s ) |2 . This is followed by a factorization of the even denominator polynomial of | G ( s ) |2 . The terms representing the left-half s-plane poles are then used to specify the final transfer function G ( s ).
It is not necessary to go through the computation mentioned above, as extensive tables of most transfer functions are available in the literature. In the popular form of active filter realizations, higher order forms are realized as cascades of second-order sections for even n, with the addition of a first order section if n is odd. The reason for this is that second-order sections are easy to design, adjust and debug, and lead to a standardized modular construction of higher order filters. The parameters of second-order sections have reasonably low sensitivity to component variations.
.
|
Table 1.1: Factored forms of low-pass filter
denominator-polynomials normalized for a cutoff wc = 1 rad/s |
|||||||||||||||||||||
| Order | |||||||||||||||||||||
| Butterworth | |||||||||||||||||||||
|
|||||||||||||||||||||
| Chebyshev 0.5 dB ripple | |||||||||||||||||||||
|
|||||||||||||||||||||
|
Chebyshev 1.0 dB ripple |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
Chebyshev 2.0 dB ripple |
|||||||||||||||||||||
|
|||||||||||||||||||||
| Chebyshev 3.0 dB ripple | |||||||||||||||||||||
|
|||||||||||||||||||||
A limited table of the factored forms of the polynomials is given in table 1.1. The table gives the factored form of the denominator polynomial for a filter having a cuto. of one radian per second, namely wc = 1 rad/s. We will first address the issue of the second-order portion of the denominator appearing in table 1.1, which we write in the form
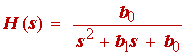
(1.25)
We have to determine the relationship of the parameters appearing in the above equation and those which are found in the design equations for second-order filters in Franco and other books. The latter are based on the parameters f 02 and Q of a second-order transfer function of the form
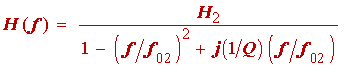
(1.26)
Different books on the subject of filter design differ in their presentation of the design polynomials. Our difficulty arises from the fact that the polynomials appearing in table 1.1, and as a consequence (1.25), are scaled for filters normalized to have wc = 1, whereas (1.26) and the tables appearing in Franco are scaled for filters normalized to fc = 1. The rescaling is performed by replacing the variable s in (1.25) with a new variable s' / 2p . This produces
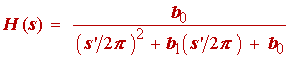
(1.27)
Substituting s' = j2p f into the above
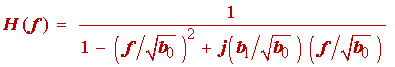
(1.28)
and comparing with (1.26) we obtain
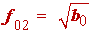
(1.29)
and
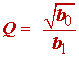
(1.30)
We will now address the issue of the first-order portion of the denominator appearing in table 1.1, which we write in the form
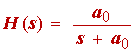
(1.31)
Again we rescale by replacing the variable s in the above with s' / 2p.
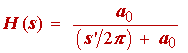
(1.32)
and then substituting s0 = j2.f into the above
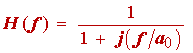
(1.33)
which is the equation for a standard first order low pass filter with the cutoff frequency
f 01 = a0
(1.34)
An example will make clear the use of table 1.1 and the above equations.
Example 3: In example 2 it was determined that we wish to realize a 0.5 dB ripple Chebyshev filter with n = 3. From table 1.1 we find that the filter should have the transfer function given by
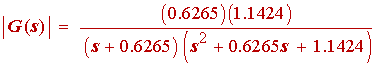
(1.35)
The transfer functions are customarily written in a form that produces a transfer function of unity at zero frequency. That is the reason for the strange looking numerator in the above expression.
Inspection of the above equation tells us that a0 = 0.6525. Hence from (1.34) we have for the first order section
f 01 = a0 = 0.6265
(1.36)
By further inspection of (1.35) we determine that b0 = 1.1424 and b1 = 0.6265. Using (1.29) and (1.30), we obtain
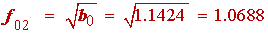
(1.37)
and
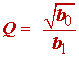
= 1.7060
(1.38)
The results of (1.36–1.38) are correct for an fc = 1 Hz. To rescale for the desired fc = 3kHz, we simply multiply the above frequencies by 3000.
We therefore wish to build a filter containing a first order section with cuto. frequency
f 01 = 1.880 kHz
(1.39)
and a second-order section specified by the two parameters
f 02 = 3.206 kHz
(1.40)
and
= 1.7060 (1.41)
The remaining task is to realize the Butterworth and Chebyshev filters which were specified at the beginning of the tutorial discussion.
1.8 Examples of Filter Realizations
When we select circuits to realize the transfer functions, we have a number of choices. For the first-order section we can use a simple passive RC circuit or a first order active circuit. The latter has the advantage that loading problems are avoided. For the second-order section we have a very wide choice including the well known Sallen-Key, KRC, state variable, and the biquad filter. The choice among them is based on such factors as simplicity, ease of adjustment, sensitivity to the variation of the values of the resistors and capacitors, and non-ideality of the Op Amp. If 4Qf0 << ft , the gain-bandwidth product of the Op Amp, then the frequency response of the Op Amp does not have to be considered [see Franco p. 182]. In example 3, with f 02 = 3.206 kHz and Q = 1.706, the 4Qf0 product is equal to 21.9 kHz. This is much less than the ft of a µA741 Op Amp, which is 1 MHz. So the Op Amp frequency response should have a negligible effect on the performance of the filter.
Example 4: We will continue with the realization of the Chebyshev filter whose specifications were obtained in example 3. The specifications of this filter are reiterated here for convenience. We need a first order section with f 01 = 1.880 kHz as well as a second-order section specified by the two parameters f 02 = 3.206 kHz, Q = 1.7060.
For the realization of the second-order section, we will choose an equal-component-value KRC low-pass filter realization [see Franco pp. 125-127]. The configuration is shown in the second Op Amp section of figure 1.3. The equations which produce the component values are the following.
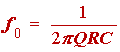
(1.42)
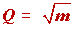
(1.43)
Substituting into (1.43) we get m = 2.91. Choosing (quite arbitrarily) C = 0.001 µF, we find upon substitution into (1.42) that R = 29.1 kW. For the latter we choose the nearest available 5% resistance value to get R = 30 kW. This gives us the value of mR = 87.3 kW, with the closest 5% choice being mR = 91 kW. The complete design is shown in figure 1.3. For RA we chose 240 kW, so that the resistance to ground from the negative terminal of the Op-Amp will equal that from the positive terminal. This is done in order to minimize the DC offset at the input terminals (and consequently at the output terminal.)
For the first order section we will choose a low-pass filter with gain [see Franco p. 106]. The design equation is merely
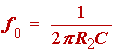
(1.44)
Choosing C = 0.001 µF and using f 01 = 1.880 kHz we find that R2 = 84.7 kW. The closest 5% value is R2 = 82 kW. Since the low-frequency gain of the second-order section is 2, we will make the gain of the first-order section 1 / 2. To do this we need R1 = 164 kW. The closest 5% value that we choose for our design is R1 = 160 kW. Figure 1.3 shows the realization of the entire 3rd order 0.5 dB ripple Chebyshev low-pass filter. We chose to make R3 = 27 kW to minimize the DC offset at the input terminals.
The effect of component tolerances on the overall frequency response of the filter can be estimated by looking at the design equations. Using component values with a 5% tolerance we could have a worst case cutoff frequency variation of ±10% from its design value. If this is not acceptable then the design can be reexamined with the idea of using 1% tolerance component values. The detailed study of the changes in the shape of the filter response curve can be done using a computer simulation program such as PsPice. The simulation can also be useful for determining the effect of the non-ideality of the Op-Amp on the frequency response. By running the simulation twice, once using an ideal Op Amp and a second time using a realistic model from the PsPice library, the effect of the Op Amp frequency response on the filter becomes evident.
The biquad or Tow-Thomas filter circuit uses more components than the Sallen-Key type circuit. In return it offers some significant advantages that make it popular. Some of these are:
The values of f0, Q, and gain can be adjusted using variable resistors. The adjustment of each parameter can be made independently, that is, without affecting the values of any other parameters.
High Qs of the order of one hundred can be achieved in practice.
There are no large gains to cause saturation problems.
Equal Cs can be used.
We will now explore an alternative method for the realization of the second-order filter section.
Example 5: We turn attention entirely to the low-pass second-order filter section whose specifications were obtained in example 3. The specifications of this second-order section are reiterated here for convenience. They are f0 = 3.206 kHz and Q = 1.7060. We simplify the design equations [see Franco, p. 142] by setting R4 = R5 = R and C1 = C2 = C , to obtain
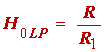
(1.45)
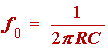
(1.46)
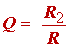
(1.47)
Choosing, arbitrarily, the convenient value C = 0.001 µF, we find from (1.46) that R = 49.6 kW. We choose the closest standard 5% value of 51 Wk. Using this value in (1.47), we find that R2 = 87 kW. We again choose the closest standard 5% value, which is 91 kW. If we wish to make the gain of this section at DC unity, then we assign R1 = 51 kW. The complete circuit is shown in figure 1.4. When designing the first order section, like the one shown in figure 1.3, we have to keep in mind that it needs to have a gain of unity since the second-order section has a gain of unity.
Figure 1.4: Tow-Thomas realization of the 2nd order section specified in example 3.
If it is necessary to adjust the values of f0, Q , and gain very precisely, adjustable resistors can be used for R5, R2 and R1 respectively. To obtain good resolution in the adjustment it is sensible to reduce the resistor’s value by about 10% and to add a series variable-resistor whose value is about 20% of the total value required. The order of adjustment is: first adjust f0 using R 5 (which will affect Q, then adjust the gain using R 1 (which will not affect f0 and Q ), and finally to adjust Q using R 11 (which will not affect f0 and the gain).
A practical way to adjust f0 is to make use of the fact that at f = f0 there is a 90° phase shift between the output and the input voltages. The gain can be adjusted at a frequency much lower than f0 (e.g f0 / 100). The value of Q can be adjusted by setting the input frequency to f0 and using the fact that at f = f0, Vo / Vi = H0LPQ.
1.9 Student’s Filter Specification
Table 1.2 will be used by the students to select the specifications of the filters to be built and tested for the duration of this laboratory. Each group will use the last four digits (designated M) of one social security number to determine the specifications of the filter which it needs to build. The following example explains how this is done.
Suppose the social security number of one member of the group is XXX-YY-3194, hence M = 3194. (M mod 3) + 1 = 3, determines column III for selecting the filter specification. M, expressed in hexadecimal form, equals 0C7AH. The last digit of this number determines the row of the table for selecting the filter specification, in this case row A.
|
Table 1.2: Filter specifications. In all cases A p ≤ 1 dB. |
|||||||||
| I | II | III | |||||||
| fp | fs | As | fp | fs | As | fp | fs | As | |
|
0 |
2.0 |
7.0 |
30 |
2.2 |
7.7 |
30 |
2.4 |
8.4 |
30 |
|
Go to EE494 Index Experiment | 1 | 2 | 3 | ECE Lab Home |
|