- 1.4 Basic Statistical Data Handling
- Errors in Quantitative Analysis
- Statistics of Repeated Measurements: Precision
The objective of environmental measurements can be qualitative or quantitative. For example, the presence of lead in household paint is a topic of concern. The question may be "Are there toxic metals present in the paint in a certain home?" An analysis designed to address this question is a qualitative analysis, where the analyst screens for the presence of a certain pollutant or class of substances. The next obvious question, of course, is "How much lead is in the paint?" This type of analysis is called quantitative analysis and it not only addresses the question of the presence of lead in the paint, but also its concentration.
Let us say that the analyst uses a technique that can measure as low as 1 m g/kg of lead in paint. For a particular sample he says that no lead was detected. This means that the concentration of lead in that sample is less than 1 m g/kg. It is not proper to report the results of this analysis as "zero lead" since it may well be present at some lower concentration, which our measuring device cannot detect. The report should read "lead not detected above 1m g/kg" or "lead not detected; detection limit 1m g/kg". Quantitative analyses of environmental samples are particularly challenging because the concentrations of pollutants in environmental samples are often very low, and the matrix is usually complex.
All numerical results obtained from experimentation are accompanied by a certain amount of error and an estimate of the magnitude of this error is necessary to validate the results. Error is a statistical term, and should not be confused with the common meaning of the word, which implies a blunder and blame to be laid on someone! All measurements have some error associated with them. One cannot eliminate it, but with careful work, the magnitude of the error can be characterized and, sometimes, the magnitude can be reduced with improved techniques.
In general, the types of error can be classified as random or systematic. If the same experiment is repeated several times, the individual measurements will fall around an average value. The differences are due to unknown or uncontrollable factors, and are termed random error. Random errors, if they are truly random, should cluster around the true value, and have equal probability of being above or below it. Chances are that the measurements will be slightly high or slightly low more often than they will be very high or very low. The measure of the amount of random error present in a set of data is the precision or reproducibility.
On the other hand, systematic error tends to deviate or bias all the measurements in one direction. So accuracy, which is a measure of deviation from the true value, is affected by systematic error. Accuracy is defined as the deviation of the mean from the true value.
Accuracy = (mean - true value) / true value ( .1)
Often the true value is not known. For the purpose of comparison, measurement by an established method or by an accepted institution is sometimes accepted as the true value. In colloquial English, accuracy and precision are often used interchangeably, but in statistics they mean quite different things.
The difference between accuracy and precision is further illustrated by the following example. A sample containing 10 m g/kg of lead is analyzed by acid digestion and atomic absorption spectrometry . Five repeat analyses are performed by four different laboratories, resulting in the data presented in Table .4 and Figure .1. The analyses performed by laboratory A show less variability but are not close to the true value. So, this laboratory’s work has high precision but low accuracy. This is a strong sign that this laboratory is subject to some identifiable source of bias. Its calibrations, standards and methods should be examined carefully. Laboratory D’s data on the other hand show little variability and good accuracy. Laboratory B and C both have data with poorer precision, but one is accurate while the other is not. Actually, for a small number of replicates, when good accuracy is obtained with poor precision, it is usually accidental!
Since every measurement contains certain amount of error, the result from a single
measurement can not be accepted alone as a true value. An estimate of the error is
necessary to predict within what range the true value may lie. The random error in a
measurement is estimated by repeating the measurement several times, which provides two
valuable pieces of information: the average value and the variability of the
measurement. The most widely used measure of average value is the arithmetic mean, ![]() ,
,
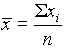 (
.2)
(
.2)
where S xi is the sum of the replicate measurements and n is the total number of measurements.
The most useful measure of variability (or precision) is the standard deviation, s . This is calculated as:
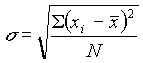 (
.3)
(
.3)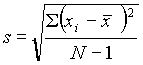 (
.4)
(
.4) ( .6)
( .6)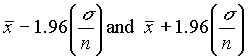 . This is the 95% confidence interval, i.e. there is a 95% probability
that the true value lies within this range. Similarly, the 99.7% confidence interval falls
between
. This is the 95% confidence interval, i.e. there is a 95% probability
that the true value lies within this range. Similarly, the 99.7% confidence interval falls
between 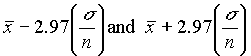 .
. 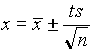 (
.8)
(
.8)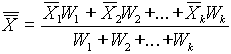 ( .9)
( .9)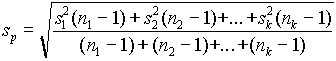 ( .12)
( .12) 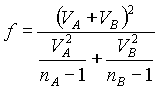 (
.16)
(
.16)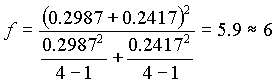
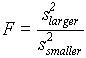 ( .18 )
( .18 )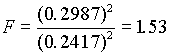
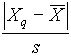 .
.