Welcome to the NJIT Applied Mathematics Capstone webpage! Over the course of the school year, we carried out experimental, theoretical, and computational studies of Saffman-Taylor instability in a Hele-Shaw flow involving injection of a less viscous fluid into a more viscous one in a thin gap between two plates. What one finds in such experiments is pattern formation reminiscent of dendritic structures formed from diffusion limited aggregation simulations.

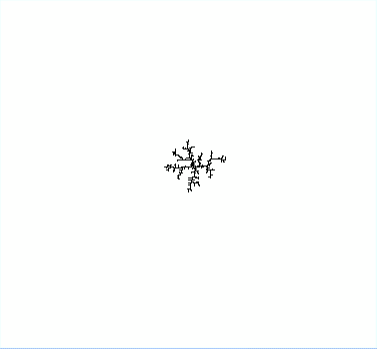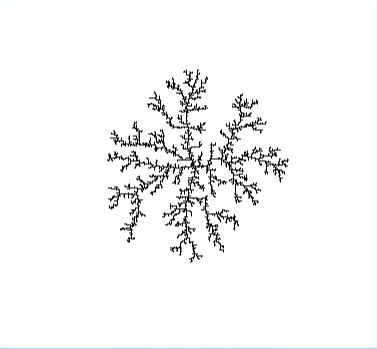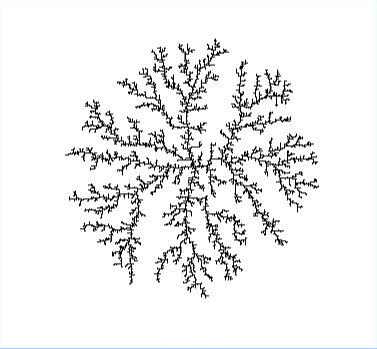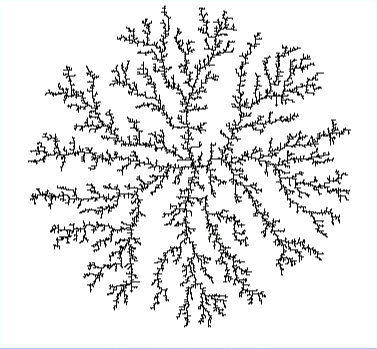
To characterize the properties of the emerging patterns, we use several methods to calculate the fractal dimension based on the data collected from experimental trials and extensive simulations that were modified to account for the non-Newtonian behavior. We fit simulation parameters to experimental videos using stochastic optimization techniques including the downhill simplex method and brute force searches. We further quantify the instability development in both the experiments and simulations using Fourier analysis and compare the results to the analytical ones obtained by linear stability analysis.

How is this study relevant? Well, in 1981, Tom Witten and Len Sander proposed diffusion limited aggregation (DLA) as a viable model to capture transport phenomena when diffusion is the dominant process over convection. Examples of such things happening in nature are numerous, e.g. electric deposition, river networks, crystal growth, and viscous flow in porous media. Such structures exhibit scale invariance and fractional dimensions as defining features. Much of the theoretical work that has been invested in studying the connection of DLA to self-similarity in nature has been attributed to the renormalizability of the Hamiltonian involved in non-equilibrium statistical mechanics, yet scientists are still puzzled about many aspects of the DLA model. We look to further understand this important theoretical development by studying its connection to the Hele-Shaw flow experiment.

For flow of Newtonian fluids in porous media, Darcy’s law \(u = \frac{-\kappa}{\mu}\nabla p\) governs the fluid flow velocity as a function of pressure gradient. By modeling the fluid as incompressible, this leads to the Laplace equation \(\Delta p = 0\). Remarkably, the connection of this model to DLA is immediately apparent. The pressure field satisfies the Laplace equation while the velocity of the fluid interface is proportional to gradient of the pressure for the Hele-Shaw problem. Meanwhile, the probability density of a random walker satisfies the Laplace equation, and the probability of growth at the surface is proportional to the gradient of the probability density for DLA. In essence, DLA resembles a stochastic version of the Hele-Shaw flow model.

The research we carried out is on non-Newtonian Hele-Shaw flow with an aim to establish a connection with DLA. For more information about any particular part of our project seeking to establish deeper connections between these two models, feel free to click on any of the links on the left at your leisure. This project was carried out over the 2015-2016 school year by the NJIT Applied Mathematics Capstone students and was overseen by Professor Lou Kondic. Partial support bys NSF grant No. 1211713 is acknowledged.