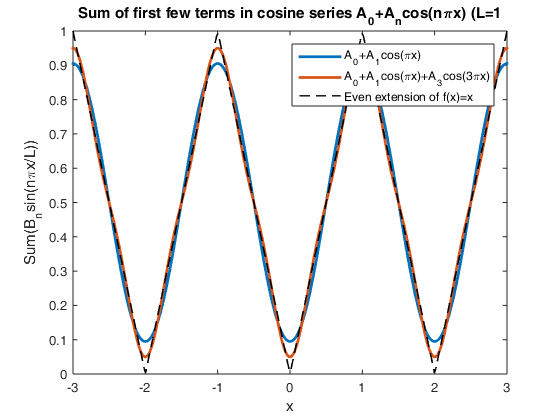
Fourier cosine series: triangular wave

Math 331, Fall 2017, Lecture 2, (c) Victor Matveev

Fourier cosine series of a simple linear function f(x)=x converges to an even periodic extension of f(x)=x, which is a traingular wave. Note the very fast convergence, compared to the sine series

clear;
hold off
L     = 1;                        % Length of the interval
x     = linspace(-3*L, 3*L, 300); % Create 300 points on the interval [-3L, 3L]
Const = -4*L/pi^2;                % Constant in the expression for A_n
Cn    = L / 2;                    % The baseline of the cosine series: A0 = L/2

for n = 1 : 2 : 3                 % Only sum over odd integers
    An = Const/n^2;               % Coefficients inversely proportional to n^2
    Fn = An * cos(n*pi*x/L);      % Calculate Fourier cosine term
    Cn = Cn + Fn;                 % Add the term to Fourier cosine series sum
    plot(x, Cn, 'linewidth', 2);  % Plot the cosine fourier sum
    hold on;
end

xlabel('x'); ylabel('Sum(B_nsin(n\pix/L))');
title('Sum of first few terms in cosine series A_0+A_ncos(n\pix) (L=1');
plot(x, abs(mod(x+1,2)-1),  'k--', 'linewidth', 1); % Trickiest part of the code: create triagular wave
legend('A_0+A_1cos(\pix)', 'A_0+A_1cos(\pix)+A_3cos(3\pix)', 'Even extension of f(x)=x');