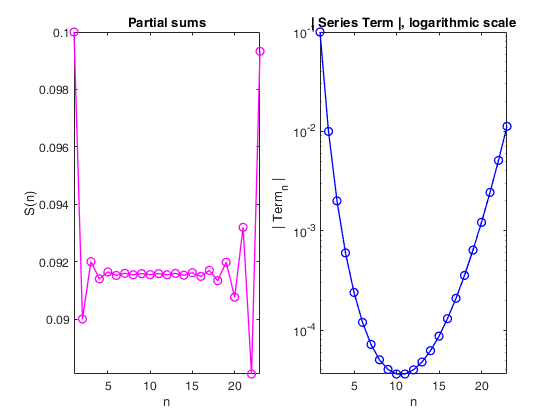
Compute the Asymptotic Series
Math 613 o Fall 2019 o Victor Matveev o Homework #5 o Problem 1
clear;
x = 0.1;
N = 23;
T = zeros(N, 1);
S = zeros(N, 1);
T(1) = x;
S(1) = x;
for n = 2 : N
T(n) = -T(n-1) * (n - 1) * x;
S(n) = S(n-1) + T(n);
end
subplot(1,2,1);
plot(1:N, S, 'mo-', 'linewidth', 1);
xlabel('n'); ylabel('S(n)');
title('Partial sums');
axis tight;
subplot(1,2,2);
plot(1:N, abs(T), 'bo-', 'linewidth', 1);
xlabel('n'); ylabel('| Term_n |');
title('| Series Term |, logarithmic scale');
set(gca, 'yscale', 'log');
axis tight;