Symbolic algebra computation of perturbative series
Math 613 o Fall 2019 o Victor Matveev o Homework 5 o Problem 2
clear;
N = 6;
syms eps Y t;
yn = sym('y', [N+1, 1]);
Y = yn(1);
for n = 1 : N
Y = Y + eps^n * yn(n+1);
end
T = 1; DY = 1;
for n = 1 : N
T = -T * eps * Y / (2*n*(2*n-1));
DY = DY + T;
end
DY = coeffs(expand(DY), eps);
fprintf('\n>>> Print differential equations: \n');
for n = 1 : N
fprintf('y_%d''(t) = %s\n', n-1, DY(n) );
end
yt = 1 + t;
for n = 2 : N
for m = n : N
DY(m) = subs(DY(m), yn(n-1), yt);
end
yn(n-1) = yt;
yt = simplify( expand( int( DY(n), t) ) );
end
yn(N) = yt;
fprintf('\n>>> Print the results: \n');
for n = 1 : N
fprintf('y_%d(t) = %s\n', n-1, yn(n) );
end
TT = linspace(0, 40, 400);
figure; hold on;
SS = 0;
eps = 0.1;
str = { };
for n = 1 : N
YY = eval( subs( yn(n), t, TT) );
SS = SS + eps^(n-1)*YY;
plot(TT, SS, 'linewidth', n/2);
str = [str, ['S_', num2str(n)]];
end
legend(str);
xlabel('time'); ylabel('S_n(t)');
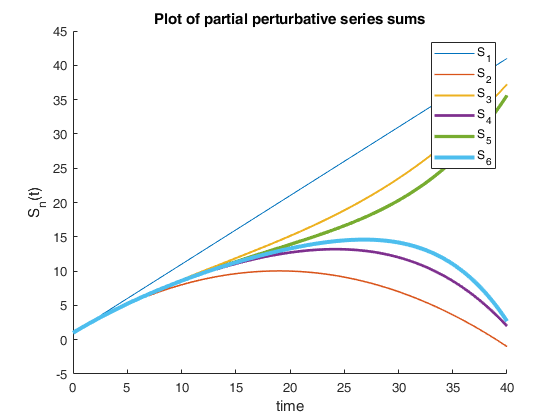
title('Plot of partial perturbative series sums');
>>> Print differential equations:
y_0'(t) = 1
y_1'(t) = -y1/2
y_2'(t) = y1^2/24 - y2/2
y_3'(t) = (y1*y2)/12 - y3/2 - y1^3/720
y_4'(t) = (y1*y3)/12 - y4/2 - (y1^2*y2)/240 + y2^2/24 + y1^4/40320
y_5'(t) = (y1*y4)/12 - y5/2 + (y2*y3)/12 - (y1*y2^2)/240 - (y1^2*y3)/240 + (y1^3*y2)/10080 - y1^5/3628800
>>> Print the results:
y_0(t) = t + 1
y_1(t) = -(t*(t + 2))/4
y_2(t) = (t*(12*t + 4*t^2 + 3))/72
y_3(t) = -(t*(24*t + 36*t^2 + 9*t^3 + 1))/720
y_4(t) = (t*(384*t + 2008*t^2 + 1760*t^3 + 352*t^4 + 3))/120960
y_5(t) = -(t*(1920*t + 30760*t^2 + 73920*t^3 + 45408*t^4 + 7568*t^5 + 3))/10886400