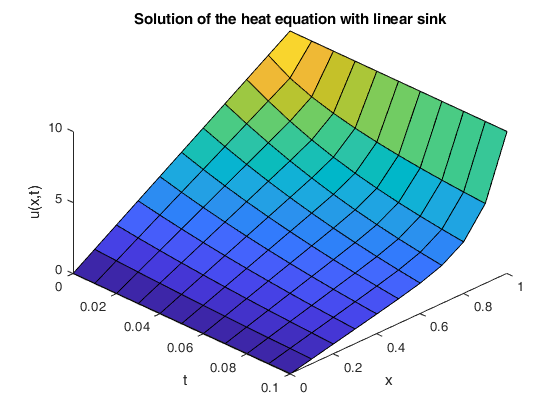
Solving heat equation using finite differences

Math 613 o Fall 2019 o Victor Matveev o Homework 6 o Problem 3

clear;
N      = 10;          % Number of space partitions
M      = 10;          % Number of time  partitions / steps

gamma  = 10;          % Model parameters (feel free to change)
Length = 1;           % Length of the cable / rod / tube
D      = 0.2;         % Diffusion coefficient
dt     = 0.01;        % Delta t
dx     = Length / N;  % Delta x

u0     = @(x) 10*x;   % Initial condition, defined as an in-line function
uLeft  = u0(0);       % Boundary condition on the left  = u0(0) = 0
uRight = u0(Length);  % Boundary condition on the right = u0(L) = L = 10

s  =  D*dt/dx^2;      % Stencil parameter s
p  =  gamma*dt;       % Stencil parameter p
k  =  1 - 2*s - p;    % Central stencil parameter k = 1 - 2s - p

% %%%%%%%%% First, construct and initialize the solution array: %%%%%%%%%%%

u = zeros(N+1, M+1);  % Create solution array variable
u(  1, :) = uLeft;    % Boundary condition on the left (indexing starts at 1 in MATLAB)
u(N+1, :) = uRight;   % Boundary condition on the right
xArray = dx*(0:N);    % Array of x-values (for the plot and IC calculation)
tArray = dt*(0:M);    % Array of t-values (for the plot)

for n = 2 : N
    u(n, 1) = u0(xArray(n)); % Compute initial condition (see above)
end

% %%%%%%%%%%%%%%%%%%%%% Now, solve the PDE (easy!!) %%%%%%%%%%%%%%%%%%%%%%

for m = 1 : M
    for n = 2 : N
        u(n, m+1) = s*(u(n-1, m) + u(n+1, m)) + k*u(n, m);
    end
end

% %%%%%%%%%%%%%%%%%%%  Finally, plot the results:  %%%%%%%%%%%%%%%%%%%%%%%%

[X, T] = meshgrid(xArray, tArray);
figure; hold on;
surf(T, X, u');
view(45, 45);
xlabel('t'); ylabel('x'); zlabel('u(x,t)');
title('Solution of the heat equation with linear sink');