Solving Burger's wave equation using finite differences

Math 613 o Fall 2019 o Victor Matveev o Homework 8 o Problem 3

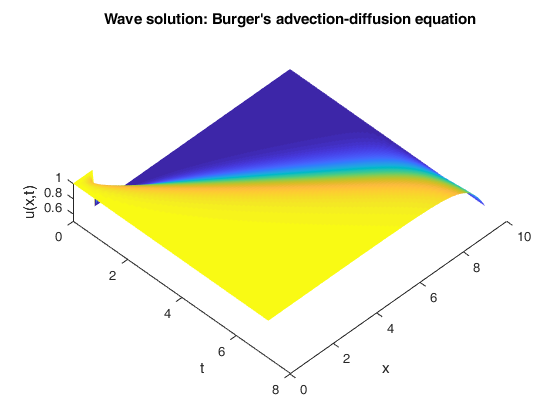
clear;
N      = 100;         % Number of space partitions
M      = 2400;        % Number of time  steps

Length = 10;          % Length of the cable / rod / tube
dt     = 0.003;       % Delta t
dx     = Length / N;  % Delta x

uLeft  = 1;           % Boundary condition on the left  = u0(0) = 0
uRight = 1/2;         % Boundary condition on the right = u0(L) = 1/2

s  =  dt / dx^2;      % Stencil parameter s (from the diffusion term)
k  =  dt / (2*dx);    % Stencil parameter k (from the advection term)

% %%%%%%%%% First, construct and initialize the solution array: %%%%%%%%%%%

u = zeros(N+1, M+1);  % Create solution array variable
u(  1, :) = uLeft;    % Boundary condition on the left (indexing starts at 1 in MATLAB)
u(N+1, :) = uRight;   % Boundary condition on the right

u(1:10, 1) = uLeft;   % Set the initial condition on the  left side of tube
u(11:N, 1) = uRight;  % Set the initial condition on the right side of tube

% %%%%%%%%%%%%%%%%%%%%% Now, solve the PDE (easy!!) %%%%%%%%%%%%%%%%%%%%%%

for m = 1 : M
    for n = 2 : N
        u(n, m+1) = s*(u(n-1, m) + u(n+1, m)) + (1 - 2*s)*u(n, m) - k*(u(n+1, m)^2 - u(n-1, m)^2);
    end
end

% %%%%%%%%%%%%%%%%%%%  Finally, plot the results:  %%%%%%%%%%%%%%%%%%%%%%%%

[X, T] = meshgrid( dt*(0:M), dx*(0:N));
figure; hold on;
surf(X, T, u);
shading flat;
view(45, 80);
xlabel('t'); ylabel('x'); zlabel('u(x,t)');
title('Wave solution: Burger''s advection-diffusion equation');

% %%%%%%%%%%%%%%%%%%%  Calculate the wave speed:  %%%%%%%%%%%%%%%%%%%%%%%%%

I1 = find( u(:,  500) < 0.75, 1);  % Find middle of the wave at t =  500*dt
I2 = find( u(:, 1500) < 0.75, 1);  % Find middle of the wave at t = 1500*dt
Speed = (I2 - I1)*dx / (1000*dt);
fprintf("Wave speed = %g\n", Speed);

Wave speed = 1.5

Published with MATLAB® R2018b