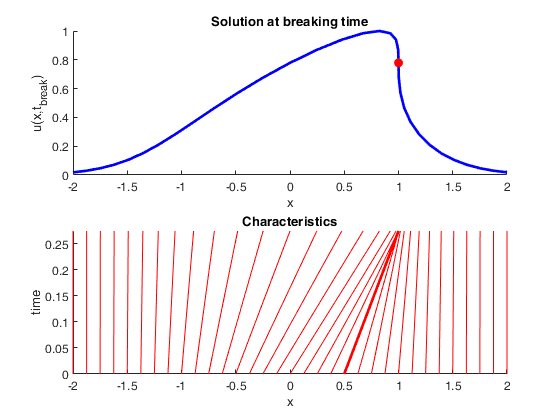
Plot characteristic and solution without solving in closed-form
Math 613 o Fall 2019 o Victor Matveev o Homework 8 o Problem 1
clear;
M = 33;
L = 2;
tShock = exp(1/2)/6;
x0Array = linspace(-L, L, M);
xArray = [];
subplot(212); hold on;
for x0 = x0Array
u0 = exp(-x0^2);
Velocity = 3*u0.^2;
xAtShock = x0 + tShock * Velocity;
xArray = [xArray, xAtShock];
if abs(x0 - 0.5) < 0.1
plot([x0 xAtShock], [0 tShock], 'r-', 'linewidth', 2);
else
plot([x0 xAtShock], [0 tShock], 'r-');
end
end
axis([-L L 0 tShock]);
xlabel('x'); ylabel('time');
title('Characteristics');
subplot(211); hold on;
plot(xArray, exp(-x0Array.^2), 'b-', 'linewidth', 2);
plot(0.5 + tShock * 3*exp(-1/2), exp(-0.5^2), 'ro', 'MarkerFaceColor', 'r');
axis([-L L 0 1]);
xlabel('x'); ylabel('u(x,t_{break})');
title('Solution at breaking time');