Inelasticity in Rubber-like Materials
ABSTRACT: Filled rubber-like materials are important engineering materials, and they are widely used in aerospace, automotive, and other industries. However, their nonlinear, inelastic, and rate-dependent constitutive behavior is not fully understood and modeled with varying degrees of success. Much of the previous literature has focused on either capturing quasi-static stress-softening behavior or rate-dependent viscous effects, but generally not both concurrently. We have developed a thermodynamically consistent constitutive model which accounts for both of those phenomena concurrently, as well as thermal recovery. A set of comprehensive mechanical tensile tests were conducted, and the constitutive model was then calibrated to the experimental data. The model was numerically implemented into the finite element package Abaqus by writing a user material subroutine UMAT. The constitutive model was validated by comparing a numerical simulation prediction with an inhomogeneous deformation experiment.
Details:
Combined viscoelasticity and Mullins effect
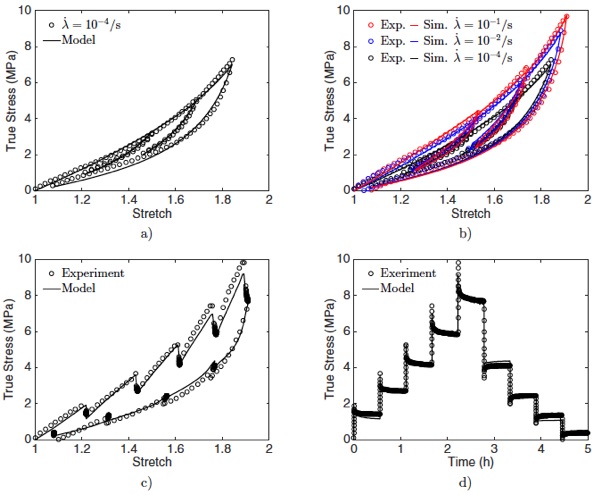
Model calibration results using virgin Viton specimens, experiments are shown as open circles and the calibrated model as solid lines. a) Quasi-static load/unload/reload test, b) load/unload/reload uniaxial tension tests at different stretch rates, and multi-step relaxation c) stress - stretch and d) stress - time.

Comparison between the experimentally measured and simulated vertical component of Hecnky strain. The left half of each subfigure shows the measured strain from DIC, while the right half of each subfigure shows the numerically computed strain. The results are shown at displacements of (left) 15.14mm, (center) 28.90mm, and (right) 37.98mm.
Thermal recovery of the Mullins effect
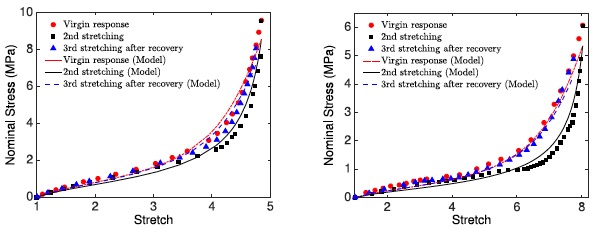
Model calibration of a rubber-like material with two different amounts of crosslinker, where experiments are shown with markers and the model with lines.