Industrial Cost Analysis: MNET 414

Solution for Home work # 2

Chapter 4

NOTE

1. ONLY ONE OR TWO ALTERNATIVE SOLUTION METHODS ARE SHOWN HERE FOR HOMEWORK PROBLEMS. EACH PROBLEM CAN BE SOLVED IN MANY OTHER ALTERNATIVE WAYS WHICH SHOULD GIVE YOU CORRECT & PRACTICALLY THE SAME ANSWER.

2.  YOU ARE LEARNING 'A' & 'G' SERIES, SO YOU SHOULD TRY TO APPLY 'A' & 'G' SERIES FORMULAS WHERE EVER APPLICABLE.

4.32. A man borrowed $500 from a bank on October 15th. He must repay the loan in 16 equal monthly payments, due on 15th of each month, begining November 15th. If interest is computed at 1% per month, how much must he pay each month?

P = $500, i = 1%, n = 16, A = ?

A = 500(A/P,1%,16) = 500(0.0679) = $33.95

4.115. A local finance company will loan$10,000 to a homeowner.  It is to be repaid in 24 monthly payments of $499 each.  The first payment is due 30 days after the $10,000 is received.  What interest rate per month are they charging?

P = $10,000, A= $499, n = 24, i = ?

10000 = 499(P/A, i, 24)
or, (P/A, i, 24) = 10000/499 = 20.04.

By checking the interest tables for P/A values at n= 24 at different interest rates, we find the following:
(P/A, 1-1/-1/4%, 24) = 20.624
(P/A, 1-1/2%, 24) = 20.030
(P/A, 1-3/4%, 24) = 19.461

So we see that the interest rate must be between 1-1/4% and 1-1/2%.  As the P/A factor 20.04 is very close to (P/A, 1-1/2%, 24) = 20.030, the interest rate the homeowner is getting is approximately 1-1/2%.

4.4. for the diagrams (a) through (d) compute the unknown values: W, X, Y, Z respectively.
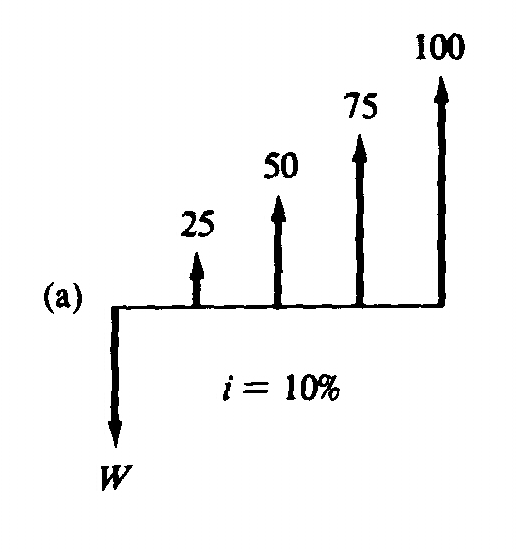46A.JPG (82054 bytes) (a)  The upper cash flow is a combination of a uniform series A = $25 and an arithmetic series G = $25 with n = 4, where W is the present worth.

W = A(P/A, i, n) + G(P/G, i, n)

or, W = 25(P/A, 10%, 4) + 25(P/G, 10%, 4)

or, W= 25(3.170)+25(4.378) = $188.70
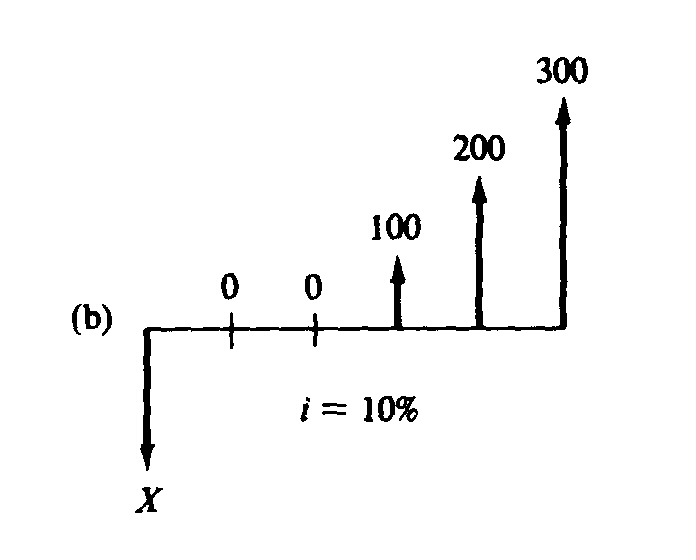46B.JPG (103333 bytes)  

(b) Here the upper cash flow is an arithmetic series of G = 100.

If we find the present worth of this series, we would get the equivalent at the period one year ahead of X.  So, P = G(P/G, 10%,4) = 100(4.378) = 437.80

With respect to X, this 437.80 is one period in future.  So,

X = 437.80(P/F,10%,1) = 437.80(.9091) = $398.09
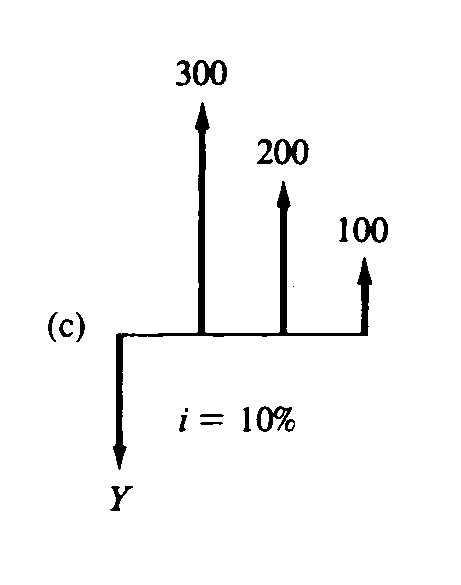46C.JPG (72721 bytes)  

(c) Here the upper cash flow is a decreasing arithmetic series, which is equivalent to an uniform series with A = 300, minus an arithmetic series  of G = 100.

The present worth of this series,

Y = A(P/A)-G(P/G) = 300(P/A,10%,3)-100(P/G,10%,3) = 300(2.487)-100(2.329) = $513.20
46D.JPG (65031 bytes)  

(d) Here the upper cash flow is equivalent to a uniform series with A = 100, with a negative one time cash flow of $50 happening at period 2.

Thus the present worth of this series,

Z = A(P/A)-F(P/F) = 100(P/A,10%,3)-50(P/F,10%,2) = 100(2.487)-50(0.8264) = $207.38

 

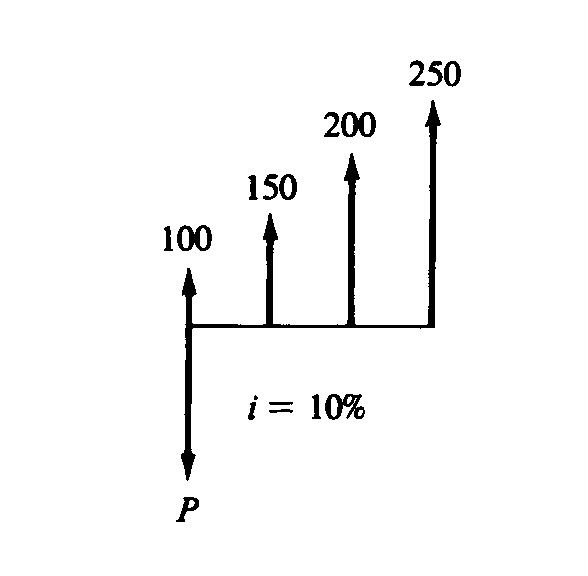
4.5. Compute the P value for the diagram below:
P = 100+150(P/A,10%,3)+50(P/G,10%,3)

= 100+150(2.487)+50(2.329) = $589.50

4-9.JPG (87399 bytes)

4.49.  A company expects to install smog control equipment on the exhaust of a gasoline engine.  The local smog control district has agreed to pay to the firm a limp sum of money to provide for the cost of the equipment and maintenance during its ten-year useful life.  At the end of ten years, the equipment which initially cost $10,000, is valueless.  The company and smog control district have agreed that the following are reasonable estimates of the end-of-year maintenance costs:

Year 1

2

3

4

5

$500

100

125

150

175

Year 6

7

8

9

10

$200

225

250

275

300

Assume interest rate is 6% per year, how much should the smog control district pay to the company now to provide for the first cost of the equipment and its maintenance cost for ten years?

The cash flow diagram will look like this

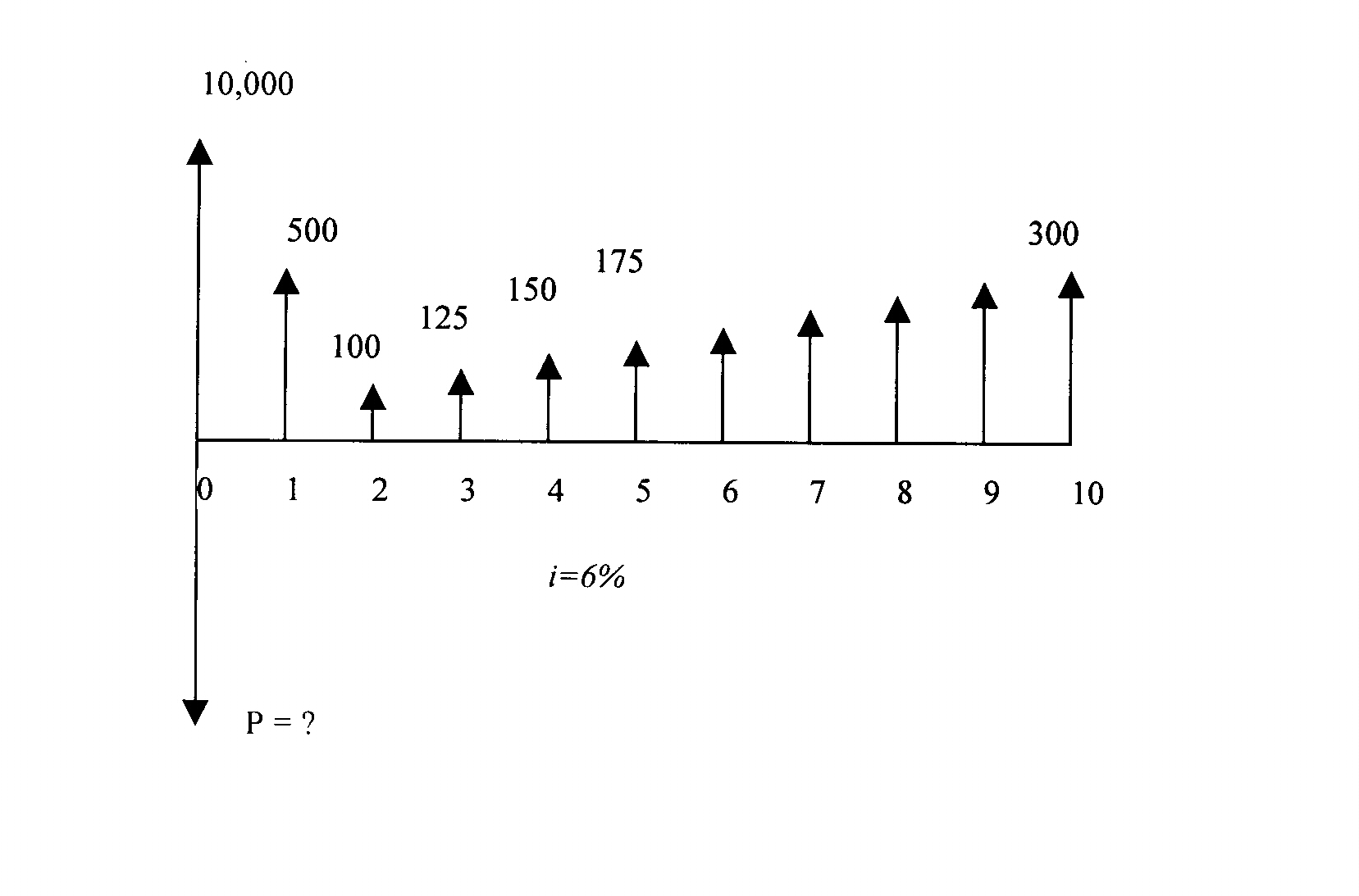
:4_36.JPG (406897 bytes)

If we split the cash flow 500 in period 1 into 75+ 425, then the upper cash flow is equivalent to a uniform series of A = 75 for 10 years, an arithmetic series of G= 25 for 10 years, a single cash flow of $10,000 in the year 0, and another single period cash flow of $425 in year 1. So the present worth of the above cash flow is

P = 10,000 + 425(P/F,6%,1) + 75(P/A,6%,10) + 25(P/G,6%,10)

P = 10,000+425(.9434)+75(7.360)+25(29.602) = 11693

4.86.  On January 1st. Frank Jenson bought a used car for $4,200 and agreed to pay it as follows: 1/3rd. down payment; balance to be paid in 36 equal monthly payments; the first payment due February 1st; an annual interest rate of 9%, compounded monthly.

a. What is the amount of Frank's monthly payment?

b. During the summer, Frank made enough money that he decided to pay off the entire balance due on the car as of October 1st.  How much did Frank owe on October 1st?

a. Frank's car cost = 4200, down payment = 4200*(1/3) = 1400.  Thus the car loan after 1/3 down payment was = 4200-1400 = $2800
This amount has to be paid back in 36 uniform payments at an interest rate 9/12 = 3/4% per month.

Thus the monthly payments should be = 2800(A/P, 3/4%, 36) = 2800(.0318) = $89.04

b. Up to September 1st.  Frank has made 8 payments.  So, 36-8=28 more payments are to be made. 

 

 

Out of these, one payment is due on 1st. October (the 9th period), and 27 more payments on the following months.  So if he wants to pay off the entire loan on 1st October, then he has to pay October's payment, plus the equivalent amount of the following 27 A- series payments.

Thus the payments required to pay off the loan P = 89.04 + 89.04(P/A,3/4%,27) = 89.04 + 89.04(24.360) = $2,258.05

Alternative solution:

 

 

Equating the loan with the present worth of the payments at period '0':

2800 = 89.04(P/A,3/4%,8) + F(P/F,3/4%,9)
or, 2800 = 89.04(7.737) + F(0.9350)
or, F(0.9350) = 2800 - 89.04(7.737) = 2111.098
or, F = 2154.97/0.9350 = 2257.86

The small difference between the two answers is due to rounding off error.

4.87. On January 1st., Laura Brown borrowed $1000 from the Friendly Finance Company.  The loan is to be repaid by four equal payments which are due at the end of March, June, September, and December.  If the finance company charges 18% interest, compounded quarterly, what is the amount of each payment?  What is the effective annual interest rate?

Payment to be made every three months, that is quarterly.  The interest is also charged quarterly at a rate of 18%/4 = 4.5%

So, the amount of 4 uniform payments are A = P(A/P,4.5%,4) = 1000(0.2787) = $278.70

The effective interest over the year = (1+r/m)m - 1 = (1+0.045)4-1 = 19.25%