Math 112 Honors: MATLAB Assignment 1

NUMERICAL INTEGRATION Due Date: March 3, 2011

Contents

Sample Program

The sample program below uses the left-endpoint rule, the right-endpoint rule and the trapezoid rule to approximate the definite integral of the function.

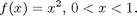
$$f(x)=x^2, \, 0<x<1.$$

Matlab comments follow the percent sign (%)

a= 0;
b= 1;
N = 10;
h=(b-a)/N;
x=[a:h:b];  %creates a vector of n+1 evenly spaced points
f=x.^2;
IL=0;
IR=0;
IT=0;
for k=1:N;  %Note that the vector f has (N+1) elements
    IL=IL+f(k);
    IR=IR+f(k+1);
    IT=IT+(f(k)+f(k+1))/2;
end;
IL=IL*h;
IR=IR*h;
IT=IT*h;

fprintf(' When N = %i, we find:\n',N);
fprintf(' Left-endpoint approximation = %f.\n',IL);
fprintf('Right-endpoint approximation = %f.\n',IR);
fprintf('   Trapezoidal approximation = %f.\n',IT);
% Output from this program:

 When N = 10, we find:
 Left-endpoint approximation = 0.285000.
Right-endpoint approximation = 0.385000.
   Trapezoidal approximation = 0.335000.

New Matab ideas

Parameters used in this program:

Your assignment

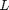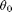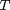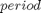A simple pendulum consists of a mass that swings in a vertical plane at the end of a massless rod of length $L$. Suppose that the pendulum is released from rest displaced through an initial angle $\theta_0$. In the absence of friction, the time $T$ required for the pendulum to make a complete swing, called the $period$, is:

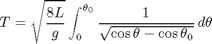
$$T=\sqrt{\frac{8L}{g}}\int_0^{\theta_0}\frac{1}{\sqrt{\cos \theta - \cos \theta_0}}\, d\theta$$

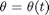where $\theta = \theta(t)$ is the angle the pendulum makes with the vertical at time $t$.

(a) Obtain a proper integral by substituting:

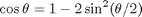
$$\cos \theta = 1 - 2\sin^2(\theta/2)$$

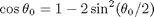
$$\cos \theta_0 = 1 - 2\sin^2(\theta_0/2)$$

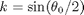
$$k = \sin(\theta_0/2)$$

and then making the change of variable:

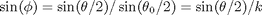
$$\sin(\phi) = \sin(\theta/2)/\sin(\theta_0/2) = \sin(\theta/2)/k$$

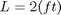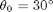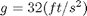(b) Evaluate the resulting integral from part (a) using the numerical integration to approximate the period of the pendulum for $L=2 (ft)$, $\theta_0 = 30^{\circ}$, and $g=32 (ft/s^2)$.

(c) For part (b), answer the following questions:


Published with MATLAB® 7.8