Math 112 Honors: MATLAB Assignment 2
TAYLOR SERIES AND POLYNOMIALS Due Date: April 18, 2011
The sample program below calculates 2nd and 4th degree Taylor polynomials for the function
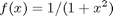
about the point
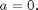
The polynomials are plotted, together with the function, over the interval
![$$[-1,1]$$](matlab2_eq64124.png)
Contents
Sample program
Lines beginning with a percent sign (%) are comments construct Taylor polynomials.
figure(1);clf; %open figure one and clear any plots x=[-1: .01:1]; y=(1+x.^2).^(-1); %the function P2=1-x.^2; %the second-order Taylor polynomial (calculated by hand) P4=1-x.^2+x.^4; %the 4th order Taylor polynomial % annotating the graph is always important figure(1);clf; %open and clear the 1st figure plot(x,y,x,P2,'--',x,P4,'-.') legend('1/(1+x^2)','P_2','P_4') xlabel('x') title('The function and the 2^{nd} and 4^{th} order Taylor Polynomials') figure(2);clf; %open and clear the 2nd figure plot(x,abs(y-P2),x,abs(y-P4),'--') % abs is the absolute value legend('|1/(1+x^2)-P_2|','|1/(1+x^2)-P_4|') xlabel('x') title('Errors in the two Taylor Polynomials') % Program output:
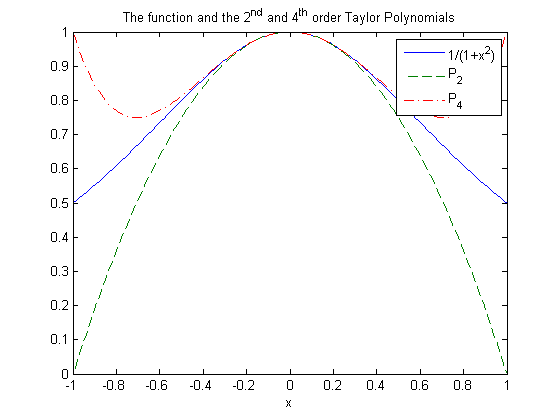
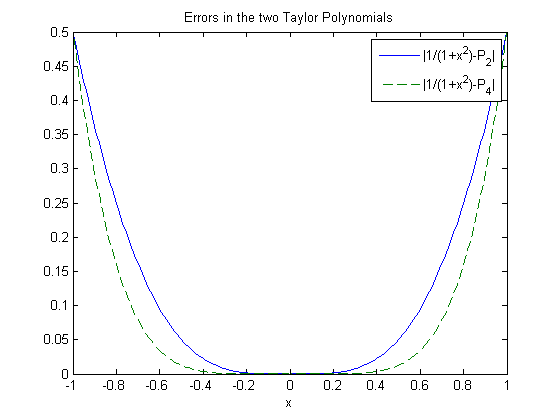
New Matlab Idea
the Legend command generates a legend for your graph. If there are two curves in your graph, the legend command should consist of two strings (defined using single quotation marks). Note that the underscore ('_') is used to make subscripts and the caret ('^') is used to make superscripts. if you want to create a superscript with more than one character in it, enclose the superscripted text in braces ('{}')
For example, to type
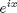
you would use the string 'e^{ix}'.
Variables used
- x, y: the independent and dependent variables
- P2, P4: the 2nd and 4th order Taylor polynomials
Your assignment: Radiation from the Stars
A  is a system that absorbs all the radiation that falls on it. Proposed in the late 19th century, the Rayleigh-Jeans Law expresses
the energy density of blackbody radiation of wavelength
is a system that absorbs all the radiation that falls on it. Proposed in the late 19th century, the Rayleigh-Jeans Law expresses
the energy density of blackbody radiation of wavelength 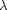 as:
as:
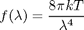
where 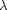 is measured in meters,
is measured in meters, 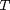 , temperature, in kelvins, and
, temperature, in kelvins, and 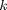 is the Boltzmann's constant. The Rayleigh-Jeans Law agrees with experiments for long wavelengths but disagrees drastically
for short wavelengths. [The experiments show that
is the Boltzmann's constant. The Rayleigh-Jeans Law agrees with experiments for long wavelengths but disagrees drastically
for short wavelengths. [The experiments show that 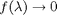 as
as 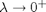 ]. The Planck's Law (found by Max Planck in 1900) models the blackbody radiation better:
]. The Planck's Law (found by Max Planck in 1900) models the blackbody radiation better:
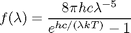
where 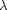 is measured in meters,
is measured in meters, 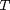 is the temperature measured in kelvins,
is the temperature measured in kelvins, 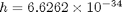 J s is Planck's constant,
J s is Planck's constant, 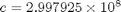 m/s is the speed of light, and
m/s is the speed of light, and 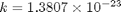 J/K is the Boltzmann's constant.
J/K is the Boltzmann's constant.
I) Show that the Planck's Law models blackbody radiation better for short wavelengths.
II) Use a Taylor polynomial to show that Planck's Law gives approximately the same values as the Rayleigh-Jeans Law for long
wavelengths. [Hint: expand the denominator of Planck's Law using Taylor series of 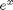 .]
.]
III) Plot the Planck's Law using 2nd and 3rd degree Taylor polynomials when approximating the denominator along with the Planck's
Law for 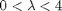
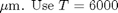 K (the temperature of the sun).
K (the temperature of the sun).
IV) Plot both laws on a same graph and comment on the similarities and differences. Use 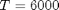 K.
K.
BONUS QUESTION: Read the Matlab help files on how to use the Symbolic Math Toolbox. This is a part of the program that can actually manipuate algebra and calculus expressions. Use the command taylor, to compute the first five terms in the Taylor series and repeat part (III).